
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистических гипотез. Критерий знаков для одной выборки. Критерий Манна – Уитни.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проверка статистических гипотез. Критерий Уилкоксона. Первая часть – стр.1 Область применения критерия Уилкоксона — анализ двух независимых выборок. Размеры этих выборок могут различаться. Назначение критерия — проверка гипотезы о статистической однородности двух выборок. Данные. Рассматриваются две выборки x1,..., xm (выборка x) и y1,..., yn (выборка y) объем ов m и n. Выборки должны быть независимыми. Обозначим закон распределения первой выборки через F, а второй — через G. Законы распределения должны быть непрерывны. Это гарантирует что не будет совпадающих значений. Гипотеза. H: F = G – однородность выборок. Альтернативы. В качестве альтернатив к H могут выступать все возможности F = G. Однако критерий Манна–Уитни способен обнаруживать отнюдь не все возможные отступления от H: F = G. Этот критерий предназначен, в первую очередь, для проверки H против альтернативы F ³ G (правосторонняя альтернатива, "перетекание" вероятностей вправо) или альтернативы F ≤ G (левосторонняя альтернатива, т.е. уход вероятностей влево). Можно рассматривать и объединение обеих возможностей (двусторонняя альтернатива). Критерий основан на ранжировании случайных величин. Для получения рангов совокупность всех наблюдений следует упорядочить в порядке возрастания (все значения различны). Последовательность действий метода: 1. Рассмотрим ранги игреков в общей совокупности выборок x и y. Обозначим их через S1,..., Sn. 2. Вычислим величину Wнабл. = S1 + · · · + Sn, называемую статистикой Уилкоксона. 3. Зададим уровень значимости α или выберем метод, связанный с определением наименьшего уровня значимости, приведенный ниже. 4. Для проверки H на уровне значимости α против правосторонних альтернатив P(xi < yj) > 0.5 найдем по таблице верхнее критическое значение W(α, m, n), т.е. такое значение, для которого P(W ³ W(α, m, n)) = α. Гипотезу следует отвергнуть против правосторонней альтернативы при уровне значимости α, если Wнабл. ³ W(α, m, n). 5. Для проверки H на уровне значимости α против левосторонних альтернатив P(xi < yj) < 0.5, необходимо вычислить нижнее критическое значение статистики W. В силу симметричности распределения W нижнее критическое значение есть n(m+n+1)−W(α, m, n). Гипотеза H должна быть отвергнута на уровне значимости α против левосторонней альтернативы, если Wнабл. ≤ n(m + n + 1) − W(α, m, n). 6. Гипотеза H отвергается на уровне 2α против двусторонней альтернативы P(xi < yj) ¹ 0.5, если Wнабл. ³ W(α, m, n) или Wнабл. ³ n(m+ n + 1) −W(α, m, n). Напомним, что альтернативы должны выбираться из содержательных соображений, связанных с условиями получения экспериментальных данных. 7. Более гибкое правило проверки H связано с вычислением наименьшего уровня значимости, на котором гипотеза H может быть отвергнута. Для разных альтернатив речь идет о вычислении вероятностей: P(W ³ Wнабл.), P(W ≤ Wнабл.), P (|W − n(m+ n + 1)/2 | ³ |Wнабл. − n(m+ n + 1)/2 |). Гипотеза отвергается, если соответствующая вероятность оказывается малой. Проверка статистических гипотез. Критерий знаков для анализа парных повторных наблюдений. Первая часть – см. стр.1. Парные повторные наблюдения – эксперименты над одной партией, или партиями, схожими друг с другом. Назначение. Критерий знаков используется для проверки гипотезы об однородности наблюдений внутри каждой пары (иногда говорят — для проверки гипотезы об отсутствии эффекта обработки). Данные. Рассмотрим совокупность случайных пар (x1, y1),..., (xn, yn) объема n. Введем величины zi = yi − xi, i = 1,...,n. Допущения. 1. Все zi предполагаются взаимно независимыми. Заметим, что мы не требуем независимости между элементами xi и yi c одинаковым номером i. Это весьма важно на практике, когда наблюдения делаются для одного объекта и тем самым могут быть зависимы. 2. Все zi имеют равные нулю медианы, т.е. P(zi < 0) = P(zi >0) = 1/2. Подчеркнем, что законы распределения разных zi могут не совпадать. Гипотеза. Утверждение об отсутствии эффекта обработки для повторных парных наблюдений (x1, y1),..., (xn, yn) можно записать в виде H: P(xi < yi) = P(xi > yi) = 0.5 для всех i = 1,..., n. Метод. 1. Перейдем от повторных парных наблюдений (x1, y1),..., (xn, yn) к величинам zi, i = 1,..., n, введенным выше. 2. К совокупности zi, i = 1,..., n применим критерий знаков для проверки гипотезы о равенстве нулю медиан распределений величин zi, i = 1,..., n. Приближение для больших совокупностей. Следует воспользоваться нормальной аппроксимацией биномиального распределения. Связанные данные. Если среди значений zi есть нулевые, то их следует отбросить и соответственно уменьшить n до числа ненулевых значений zi. Оценка эффекта обработки. Нередко для zi рассматривают модель zi = θ + ei, i = 1,..., n, где ei — ненаблюдаемые случайные величины, θ — некоторая константа, характеризующая положение одного распределения относительно другого (скажем, до воздействия и после). Эту константу часто именуют эффектом обработки. Принятые выше допущения 1 и 2 переносятся на величины e1,..., en. Гипотеза однородности формулируется в виде гипотезы о нулевом эффекте обработки H: θ = 0. Введенные величины θ и представления zi = θ + ei оказываются полезными, если в ходе проверки гипотезы выясняется, что θ = 0 и что поэтому надо оценить количественно то различие, которое привносит обработка (воздействие).
4. Проверка статистических гипотез. Анализ повторных парных наблюдений с помощью знаковых рангов (критерий знаковых ранговых сумм Уилкоксона). Первая часть – см. стр.1. Этот критерий является более мощным, чем критерий знаков. Метод. 1. Вычислим абсолютные разности |z1|,..., |zn|. Пусть Ri обозначает ранг zi в совместном упорядочении |z1|,..., |zn| от меньшего к большему. 2. Определим переменные ψi, i = 1,..., n, где
3. Вычислим наблюденное значение
4. Для одностороннего критерия для проверки H: P(zi < 0) = P(zi > 0) против правосторонней альтернативы P(zi < 0) < P(zi > 0) на уровне значимости α: • отклонить H, если Tнабл. ³ t(α, n); • принять H, если Tнабл. < t(α, n), где критическое значение t(α, n) удовлетворяет уравнению P(T ³ t(α, n) |H) = α. Для одностороннего критерия для проверки той же гипотезы против левосторонней альтернативы P(zi < 0) > P(zi > 0) на уровне значимости α: • отклонить H, если Tнабл. ≤ n(n+1)/2− t(α, n); • принять H, если Tнабл. > n(n+1)/2− t(α, n). Для двустороннего критерия для проверки той же гипотезы H против двусторонних альтернатив P(zi < 0) = P(zi > 0) на уровне значимости 2α: • отклонить H, если Tнабл. ³ t(α, n) или Tнабл. ≤ n(n+1)/2− t(α, n); • принять H, если n(n+1)/2− t(α, n) < Tнабл. < t(α, n). Приближение для большой выборки. При выполнении гипотезы H статистика
имеет асимптотическое (при n→∞) распределение N(0, 1). Приведем приближение нормальной теории для проверки H, для определенности, против правосторонней альтернативы: H отклоняется, если Tнабл. ³ zα, в противном случае H принимается. Здесь zα —квантиль уровня (1−α) стандартного нормального распределения N(0, 1). Остальные правила трансформируются аналогично. Совпадения. Если среди значений zi есть нулевые, то их следует отбросить, соответственно уменьшив n до количества ненулевых значений zi. Если среди ненулевых значений |zi| есть равные, то для вычисления T надо использовать средние ранги для величин |z1|,..., |zn| и далее использовать те же методы, что и без совпадений. Для приближения для больших выборок рекомендуется в формуле для вычисления T* значение DT заменить на
где g — число связок, t1,..., tg — их размеры. Критерий Джонкхиера. Нередко исследователю заранее известно, что имеющиеся группы результатов упорядочены по возрастанию влияния фактора. Пусть, для определенности, первый столбец таблицы значений факторов отвечает наименьшему уровню фактора, последний — наибольшему, а промежуточные столбцы получили номера, соответствующие их положению. В таких случаях можно использовать критерий Джонкхиера, более чувствительный (более мощный) против альтернатив об упорядоченном влиянии фактора. Разумеется, против других альтернатив свойства этого критерия могут оказаться хуже свойств критерия Краскела–Уоллиса. Статистика Джонкхиера. Разберем сначала, как устроена статистика этого критерия в случае, когда сравниваются только два способа обработки. Таблица факторов в этом случае имеет два столбца. Фактически здесь речь идет о проверке однородности двух выборок. Эта задача решалась с помощью статистики Манна-Уитни. Пусть имеется 2 выборки различной длины.
Обратившись теперь к общему случаю, когда сравниваются k способов обработки, поступим следующим образом. Для каждой пары натуральных чисел u и v, где 1 ≤ u < v ≤k, составляем по выборкам с номерами u, v статистику Манна–Уитни.
Определяем статистику Джонкхиера J как сумму статистик Манна-Уитни. Свидетельством в пользу альтернативы упорядоченности эффектов (против гипотезы однородности) служат большие значения статистики J, полученные в эксперименте. Для больших выборок в отношении J действует нормальная аппроксимация:
Свидетельство против гипотезы однородности – большие значения статистики:
Временной ряд Временной ряд — это последовательность чисел; его элементы — это значения некоторого протекающего во времени процесса. Они измерены в последовательные моменты времени, обычно через равные промежутки. Элементы временного ряда, — нумеруют в соответствии с номером момента времени, к которому они относятся (например, x1, x2, x3 и т.д.). Порядок следования элементов временного ряда имеет существенное значение. Нельзя переставлять элементы местами. Закономерное течение явления вмешивается случай в виде случайных импульсов, случайных помех, случайных ошибок и т.д. Поэтому изучение временных рядов — это составная часть прикладной статистики. Цели изучения временных рядов: ü краткое (сжатое) описание характерных особенностей ряда; ü подбор статистической модели (моделей), описывающей временной ряд; ü предсказание будущих значений на основе прошлых наблюдений; ü управление процессом, порождающим временной ряд. Модели тренда Линейная Полиномиальная Логарифмическая Логистическая Гомперца Полигармоническая модель Определение. Говорят, что временной ряд описывается полигармонической моделью, если он представлен в виде:
где ωk = 2π/pk, а εt является белым шумом. Случайная компонента Для описания нерегулярной компоненты и всего временного ряда в целом используют понятие случайного (стохастического) процесса или случайной последовательности (как процесса от целочисленного аргумента). Определение. Случайным процессом X(t), заданном на множестве T, называют функцию от t, значения которой при каждом t ∈ T является случайной величиной. Если T — конечное множество, то случайный процесс — это просто совокупность случайных величин. Для статистического описания такой совокупности надо указать распределение вероятностей в конечномерном пространстве. Для этого можно использовать многомерную функцию распределения или плотности, если распределение непрерывное. Если T — бесконечное множество, то для описания бесконечной совокупности случайных величин (которые в этом случае и составляют случайный процесс) применяется следующая конструкция. Определение. Говорят, что случайный процесс X(t) задан, если для каждого t из T определена функция распределения величины X(t):
для каждой пары элементов t1, t2 из T определена функция распределения двумерной случайной величины X(t1), X(t2))
и вообще для любого конечного числа элементов t1, t2,..., tn из множества T определена n -мерная функция распределения величины (X(t1), X(t2)..., X(tn))
Временной ряд Временной ряд — это последовательность чисел; его элементы — это значения некоторого протекающего во времени процесса. Они измерены в последовательные моменты времени, обычно через равные промежутки. Элементы временного ряда, — нумеруют в соответствии с номером момента времени, к которому они относятся (например, x1, x2, x3 и т.д.). Порядок следования элементов временного ряда имеет существенное значение. Нельзя переставлять элементы местами. Закономерное течение явления вмешивается случай в виде случайных импульсов, случайных помех, случайных ошибок и т.д. Поэтому изучение временных рядов — это составная часть прикладной статистики. Цели изучения временных рядов: ü краткое (сжатое) описание характерных особенностей ряда; ü подбор статистической модели (моделей), описывающей временной ряд; ü предсказание будущих значений на основе прошлых наблюдений; ü управление процессом, порождающим временной ряд.
Модели случайной компоненты Гауссовские случайные процессы. Все конечномерные распределения этих процессов являются нормальными. Для полного описания нормальных случайных процессов достаточно указать его двумерные распределения. Определение. Пусть T — множество типа t = 0, 1, 2,... или t = 0,±1,±2,... Случайный процесс X(t) называется последовательностью независимо распределенных случайных величин, если для любых наборов чисел t1, t2,..., tn Ft1,t2,...,tn(x1, x2,..., xn) = Ft1 (x1) · Ft2 (x2) ·... · Ftn(xn) Определение. Белым шумом называют временной ряд (случайный процесс) с нулевым средним, если составляющие его случайные величины X(t) независимы и распределены одинаково (при всех t). Гауссовский белый шум — это последовательность независимых нормально распределенных случайных величин со средним 0 и общей дисперсией (скажем, σ2). Процессы авторегрессии Определение. Процессом авторегрессии (первого порядка) со средним значением μ (сокращенно AR(1)) называют случайный процесс X(t), удовлетворяющий соотношению: X(t) − μ = φ · (X(t − 1) − μ) + εt, где φ и μ — некоторые числа. Марковское свойство. Поведение многих процессов в будущем определяется только их состоянием в настоящем и воздействиями на процесс, которые будут оказываться в будущем. Определение. Случайная последовательность X(t), t ∈ T называется марковской, если для любых A, B и t P(AB|X(t)) = P(A|X(t))P(B|X(t)) Стационарность. Определение. Случайный процесс X(t) называется стационарным, если для любых n, t1, t2,..., tn и τ распределения случайных величин (X(t1),...,X(tn)) и (X(t1 + τ),...,X(tn + τ)) одинаковы. Это означает, что функции конечномерных распределений не меняются при сдвиге времени, т.е.
В частности, образующие стационарную случайную последовательность случайные величины X(1),X(2),...,X(t),... распределены одинаково (но независимыми они не являются). Этот вид стационарности называют также стационарностью в узком смысле. Выборочная АКФ. Методика получения оценок значений автокорреляционной функции r(k) во многом напоминает случай двух выборок. Разберем ее устройство на оценке r(k) — корреляции между соседними членами временного ряда Xt и Xt+1. (Напомним, что большие буквы X мы используем для обозначения случайного процесса, а малые буквы x — для обозначения реализации этого случайного процесса.) Образуем из временного ряда x1, x2,..., xn совокупность из n − 1 пар: (x1, x2), (x2, x3),..., (xn−1, xn). Первый элемент каждой пары, в силу стационарности, мы можем рассматривать как реализацию случайной величины Xt, а второй — как реализацию случайной величины Xt+1. Тогда, согласно оценка коэффициента корреляции между Xt и Xt+1 может быть записана в виде:
где
соответственно оценки средних значений величин Xt и Xt+1/ При больших значениях n, учитывая что x(1) ≈ x(2)≈ x и n/(n−1) ≈ 1, это выражение часто заменяют гораздо более простым:
Аналогичнымобразом может быть определена оценка корреляции между Xt и Xt+k или k-го члена автокорреляционной функции rk:
Точность приближения заметно снижается с ростом шага k, как в силу ухудшения точности использованных выше замен, так и в силу уменьшения числа наблюдений используемых для вычисления оценки rk Поэтому на практике обычно ограничиваются изучением небольшого числа первых членов автокорреляционной функции. Вряд ли имеет смысл рассматривать оценки rk при k > n/4. Функцию rk аргумента k при k = 1, 2,... называют выборочной автокорреляционной функцией или, если не возникает недоразумений, просто автокорреляционной функцией. (При k = 0 rk по определению равно 1 и это значение обычно исключают из рассмотрения как не несущее никакой информации.) В англоязычной литературе эту функцию также называют сериальной корреляцией. График выборочной автокорреляционной функции называют коррелограммой.
На этом графике кроме значений самой функции, обычно указывают доверительные пределы этой функции в предположении, что значения автокорреляционной функции равны 0 для всех k = 0. Свойства. Изучение свойств выборочных оценок автокорреляционной функции временного ряда — в общем случае довольно сложная и до конца не решенная задача. Например выражение дисперсии оценки rk для гауссовского процесса:
Этот результат показывает, что мы не можем оценить по конечному отрезку временного ряда дисперсию оценки rk, так как она зависит от бесконечного неизвестного числа автокорреляций rt. Поэтому на практике приходится довольствоваться лишь приближениями для данного выражения. Другая проблема изучения свойств совокупности оценок rk связана с тем, что оценки с различным шагом k коррелированы между собой. Это заметно затрудняет интерпретацию коррелограммы. Рассмотрим свойства оценок автокорреляций для временного ряда, являющегося стационарной последовательностью независимых нормально распределенных случайных величин или, другими словами, гауссовским белым шумом. В этом случае для любых k, неравных нулю, по определению rk = 0. Таким образом, все слагаемые, стоящие под знаком суммы в выражении Drk, равны нулю, кроме r20 = 1. Отсюда дисперсия rk равна:
Обратим внимание на то, что оценка rk в такой форме является смещенной. Можно показать, что Другим важным свойством оценки rk является ее асимптотическая нормальность при n →∞. Такимобразом, для каждого отдельного значения rk мы можем указать приблизительный 95% доверительный интервал в виде: Они в определенной мере позволяют судить о том, насколько изучаемый процесс напоминает белый шум. Указание 95% доверительных границ для каждого коэффициента автокорреляционной функции в отдельности не означает, что с 95% вероятностью все рассматриваемые оценки rk одновременно попадают в доверительную трубку. Проверка статистических гипотез. Критерий знаков для одной выборки. Критерий Манна – Уитни. Можно высказать следующее прагматическое правило, которым руководствуются люди и которое соединяет теорию вероятностей с нашей деятельностью. • Мы считаем практически достоверным событие, вероятность которого близка к 1; • Мы считаем практически невозможным событие, вероятность которого близка к 0. Иногда то же правило высказывают чуть по"другому: в однократном испытании маловероятное событие не происходит (и наоборот — обязательно происходит событие, вероятность которого близка к 1). Слово «однократный» вставлено ради уточнения, ибо в достаточно длинной последовательности независимых повторений опыта упомянутое маловероятное (в одном опыте!) событие встретится почти обязательно. Какую вероятность считать малой? Для каждого вида деятельности она своя. Статистическая гипотеза — это предположение о распределении вероятностей, которое мы хотим проверить по имеющимся данным. Если некоторое явление логически неизбежно следует из гипотезы, но в природе не наблюдается, то это значит, что гипотеза неверна. С другой стороны, если происходит то, что при гипотезе происходить не должно, это тоже означает ложность гипотезы. Заметим, что подтверждение следствия еще не означает справедливости гипотезы, поскольку правильное заключение может вытекать и из неверной предпосылки. Поэтому, строго говоря, косвенным образом доказать гипотезу нельзя, хотя опровергнуть — можно. Впрочем, когда косвенных подтверждений накапливается много, общество зачастую расценивает их как убедительное доказательство в пользу гипотезы. В языке это отражается так, что бывшую гипотезу начинают именовать законом. Для проверки естественнонаучных гипотез часто применяется такой принцип: гипотезу отвергают, если происходит то, что при ее справедливости происходить не должно. Проверка статистических гипотез происходит так же, но с оговоркой: место невозможных событий занимают события практически невозможные. Причина этого проста: пригодных для проверки невозможных событий, как правило, просто нет. Выберем уровень вероятности ε, ε > 0. Условимся считать событие практически невозможным, если его вероятность меньше ε. Когда речь идет о проверке гипотез, число ε называют уровнем значимости. Выберем событие A, вероятность которого при гипотезе меньше ε, т.е. P(A|H) < ε. (Если H — сложная гипотеза, то меньше ε должны быть все возможные при H значения вероятности A.) Правило проверки H теперь таково: На основании эксперимента мы отвергаем гипотезу H на уровне значимости ε, если в этом эксперименте произошло событие A. Таким образом, уровень значимости есть вероятность ошибочно отвергнуть гипотезу, когда она верна. Определение. Событие A называется критическим для гипотезы H, или критерием для H. Если P(A|H) ≤ ε, то ε называют гарантированным уровнем значимости критерия A для H. Определение. Распределения, с которыми мы можем встретиться в случае нарушения H, называют альтернативными распределениями, или альтернативами. (Иногда говорят также о конкурирующих распределениях и о конкурирующих гипотезах.) Какое событие выбирать в качестве критического? Событие, вероятность которого близка к 0 при гипотезе и близка к 1 при альтернативе (идеальный вариант). Пусть T - статистика критерия. Как правило, статистику T выбирают таким образом, чтобы ее распределения при гипотезе и при альтернативе как можно более различались. При проверке статистических гипотез возможны ошибочные заключения двух типов: • отвержение гипотезы в случае, когда она на самом деле верна; • неотвержение (принятие) гипотезы, если она на самом деле неверна.
Для принадлежности к тому или иному закону распределения используют критерии согласия (статистика Колмогорова, омега-квадрат, хи-квадрат Пирсона. Формулы в лекциях смотри). Если мы не можем утверждать, что выборка соответствует нормальному закону, то переход к непараметрическим методам, основанных на понятии ранжирования. Критерий знаков для одной выборки: Для его применения достаточны очень слабые предположения о законе распределения данных, такие как независимость наблюдений и однозначная определенность медианы. Напомним, что медианой распределения случайной величины ξ называется такое число θ, для которого P(ξ < θ) = P(ξ > θ) = 1/2. Пусть задано медианное значение θ. Через некоторое время мы получаем выборку и хотим установить, изменилось ли медианное значение. Гипотеза – значение не изменилось. Проверка этой гипотезы с помощью критерия знаков проводится следующим образом. Рассмотрим случайную величину X − θ. Так как, согласно гипотезе, medX = θ, то P{(X − θ) > 0} = P{(X − θ) < 0} = 1/2. В выборке xi − θ, i = 1,..., N, подсчитаем число положительных разностей и обозначимего через S. Для формализации этого алгоритма удобно ввести функцию s(x) = 1, если разность положительная, 0 в противном случае. Тогда S =
Критерий Манна-Уитни: Область применения критерия Манна–Уитни — анализ двух независимых выборок. Размеры этих выборок могут различаться. Назначение критерия — проверка гипотезы о статистической однородности двух выборок. Иногда эту гипотезу называют гипотезой об отсутствии эффекта обработки (имея в виду, что одна из выборок содержит характеристики объектов, подвергшихся некоему воздействию, а другая — характеристики контрольных объектов). Данные. Рассматриваются две выборки x1,..., xm (выборка x) и y1,..., yn (выборка y) объем ов m и n. Выборки должны быть независимыми. Обозначим закон распределения первой выборки через F, а второй — через G. Законы распределения должны быть непрерывны. Это гарантирует что не будет совпадающих значений. Гипотеза. H: F = G – однородность выборок. Альтернативы. В качестве альтернатив к H могут выступать все возможности F = G. Однако критерий Манна–Уитни способен обнаруживать отнюдь не все возможные отступления от H: F = G. Этот критерий предназначен, в первую очередь, для проверки H против альтернативы F ³ G (правосторонняя альтернатива, "перетекание" вероятностей вправо) или альтернативы F ≤ G (левосторонняя альтернатива, т.е. уход вероятностей влево). Можно рассматривать и объединение обеих возможностей (двусторонняя альтернатива). Метод. Критерий Манна–Уитни повторяет основные идеи критерия знаков и в определенном смысле является его продолжением. Он основан на попарном сравнении результатов из первой и второй выборок. Условимся, что всякое событие xi < yj обозначает «успех», а всякое событие xi > yj — «неудачу». Смысл такой терминологии может быть связан с тем, что мы предполагаем, что вторая группа лучше первой, и рады подтверждению наших представлений. Изменяя i от 1 до m и j от 1 до n, получаем mn парных сравнений элементов выборок x и y. Обозначим число успехов в этих парных сравнениях через U. Ясно, что U может принимать любое целое значение от 0 до mn. Вычислив значение Uнабл., мы можем приступить к проверке гипотезы H: 1. Зададим уровень значимости α или выберем метод, связанный с определением наименьшего уровня значимости статистики U, который описан ниже. 2. Для правосторонних альтернатив найдем по таблицам такое критическое значение Uп.(α, m, n), что P{U ³ Uп.(α, m, n)} = α. При этом критическая область для гипотезы H против правосторонних альтернатив будет иметь вид: {U ³ Uп.(α, m, n)}. При проверке H против левосторонних альтернатив надо найти критическое значение Uл.(α, m, n), такое, что P{U ≤ Uл.(α, m, n)} = α. Здесь критическая область примет вид {U ≤ Uл.(α, m, n)}. В таблицах обычно приводятся критические значения, соответствующие числам α из ряда 0.05, 0.025, 0.01, 0.005, 0.001. Ввиду дискретного характера распределения вероятностей между возможными значениями случайной величины U, приведенные выше уравнения не всегда имеют точное решение, и в таблицах они приводятся приближенно. Для вычисления по таблицам значений Uл.(α, m, n) можно воспользоваться соотношением Uл.(α, m, n) + Uп.(α, m, n) = mn, вытекающим из симметрии распределения статистики U относительно своего центра mn/2. 3. Отвергнем гипотезу H против правосторонних (левосторонних) альтернатив при попадании Uнабл. в соответствующую критическую область. 4. При проверке H против двусторонних альтернатив в качестве критического множества можно взять объединение {U ≤ Uл.(α, m, n)} ∪ {U ³Uп.(α, m, n)}, т.е. отвергнуть H, если происходит одно из двух ранее упомянутых критических событий. Ввиду уже отмеченной симметрии этому критерию можно дать вид
При таком выборе критического множества уровень значимости удваивается. Теперь он равен 2α (с теми же оговорками насчет дискретности распределения U, что были сделаны выше). В случае совпадений: В этом случае статистику U вычисляют так: к числу успехов прибавляют уменьшенное вдвое число событий вида (xi = yj). Таким образом, каждое совпадение икса и игрека считается за половину успеха. Далее с так подсчитанным числом успехов поступают так, как описано выше. При наличии совпадающих наблюдений получаемые при использовании описанных критериев выводы имеют приближенный характер, и эти приближения тем хуже (и выводы тем сомнительнее), чем больше среди наблюдений совпадающих, т.е. чем сильнее отступление от исходных математических предположений
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.123.194 (0.013 с.) |


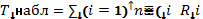
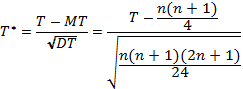


 – статистика Манна – Уитни
– статистика Манна – Уитни
 - матожидание
- матожидание – дисперсия
– дисперсия

 , обычно
, обычно 


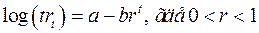
 используется в технических приложениях.
используется в технических приложениях.



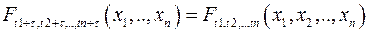







 , однако величина этого смещения стремится к нулю с ростом объема изучаемого ряда и не столь существенна в прикладном анализе.
, однако величина этого смещения стремится к нулю с ростом объема изучаемого ряда и не столь существенна в прикладном анализе. . Границы этого доверительного интервала обычно наносятся на график коррелограммы и называются доверительной трубкой.
. Границы этого доверительного интервала обычно наносятся на график коррелограммы и называются доверительной трубкой. . Случайная величина s(x) принимает два значения: 0 и 1. Согласно выдвинутой гипотезе, вероятность каждого из этих значений равна 1/2. Таким образом, видно, что задача сводится к схеме испытаний Бернулли, в которой через S обозначено число «успехов», и следует проверить гипотезу H: p = 1/2. В нашем примере надо рассматривать левосторонние альтернативы, но вообще альтернативы могут быть как односторонними, так и двусторонними, в зависимости от решаемой задачи.
. Случайная величина s(x) принимает два значения: 0 и 1. Согласно выдвинутой гипотезе, вероятность каждого из этих значений равна 1/2. Таким образом, видно, что задача сводится к схеме испытаний Бернулли, в которой через S обозначено число «успехов», и следует проверить гипотезу H: p = 1/2. В нашем примере надо рассматривать левосторонние альтернативы, но вообще альтернативы могут быть как односторонними, так и двусторонними, в зависимости от решаемой задачи.


