
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА 5. Статистическая проверка гипотез.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При статистической проверке гипотез уровнем значимости — вероятность допустить ошибку 1 – ого рода, т.е. принять правильную нулевую гипотезу +вероятность допустить ошибку 1 – ого рода, т.е. отвергнуть правильную нулевую гипотезу —вероятность допустить ошибку 2 – ого рода, т.е. отвергнуть правильную нулевую гипотезу — вероятность допустить ошибку 2 – ого рода, т.е. принять неправильную нулевую гипотезу
Критической областью называется —множество значений критерия, где + множество значений критерия, при которых — область, в которой —область, в которой
Тип (вид) критической области определяется —уровнем значимости —знаком в нулевой гипотезе —знаком +знаком неравенства в альтернативной гипотезе
По данным выборки —> или +< или —только —только <
Статистические гипотезы —выдвигаются о выборочных совокупностях, а проверяются по генеральным совокупностям —выдвигаются о выборочных совокупностях, а проверяются тоже по выборочным совокупностям +выдвигаются о генеральных совокупностях, а проверяются по выборочным совокупностям —выдвигаются о генеральных совокупностях, а проверяются тоже по генеральным совокупностям
Проверяемая гипотеза обозначается + — — —
Множество всех значений критерия, при которых — областью определения —областью принятия гипотезы +критической областью — областью существования
Форма критической области (левая, правая, двусторонняя) зависит от — гипотезы +гипотезы —сочетания —гипотезы
При статистической проверке гипотез критические точки это —множество точек, образующих область принятия —множество точек, образующих область принятия +точки, разделяющие область принятия гипотезы —область существования
Гипотеза —лежит в критической области +лежит в области принятия гипотезы —лежит в области существования —лежит на границе критической области и области принятия гипотезы
Гипотеза + лежит в критической области —лежит в области принятия гипотезы —лежит в области существования —лежит на границе критической области
При статистической проверке гипотез наблюдаемое значение критерия — определяется из таблиц +вычисляется по исходным данным —дается в условиях задачи —не используется
При статистической проверке гипотез критическое значение критерия + определяется из таблиц —вычисляется по исходным данным —дается в условиях задачи —не используется
При статистической проверке гипотез критерием называется —константа, которая находится из условий задачи —любая случайная величина +случайная величина с известным распределением —константа, которая находится из таблиц
По данным выборки +> или — < или —только —только <
По данным выборки —< или +> или — только —только <
По данным выборки —>или — только —только > +< или
При проверке гипотезы о равенстве генеральных дисперсий в качестве критерия используется случайная величина, имеющая распределение +Фишера – Снедекора (F) —Стьюдента (t) —нормальное (Z) —Пирсона
При проверке гипотезы о равенстве генеральных средних (малые выборки — Фишера – Снедекора (F) +Стьюдента (t) —нормальное (Z) —Пирсона
При проверке гипотезы о равенстве генеральных средних(большие выборки — Фишера – Снедекора (F) —Стьюдента (t) +нормальное (Z) —Пирсона
Альтернативная (конкурирующая) обозначается — — — +
Стандартный размер —> или ¹ +< или ¹ —только ¹ —только<
Уровень значимости определяет —тип критической области +размер критической области —формулировку нулевой гипотезы —формулировку конкурирующей гипотезы
Конкурирующая гипотеза определяет +тип критической области —размер критической области —распределение случайной величины, используемой в качестве критерия при проверке гипотезы —область принятия гипотезы
Если принимается гипотеза +первый станок налажен лучше —второй станок налажен лучше —станки налажены одинаково —нельзя сделать вывода
К непараметрическим относятся гипотезы —о равенстве генеральных средних — о равестве генеральных дисперсий +о законах распределения —об уровне значимости
Если конкурирующая гипотеза имеет вид +правосторонняя —левосторонняя —двусторонняя —любая
Если конкурирующая гипотеза имеет вид — правосторонняя — двусторонняя +левосторонняя —любая
Если конкурирующая гипотеза имеет вид — любая +двусторонняя —правосторонняя —левосторонняя
Если конкурирующая гипотеза имеет вид +двусторонняя — левосторонняя —любая —правосторонняя
Двусторонняя критическая область соответствует гипотезе — — + —
Если принимается гипотеза —первый станок налажен лучше —второй налажен лучше —станки налажены неодинаково +станки налажены одинаковы
Если принимается гипотеза +все детали соответствуют стандарту —тяжелее стандарта —легче стандарта —нельзя сделать вывода
Малые выборки — — + —
Большие выборки — + — —
При статистической проверке гипотезы о равенстве генеральных дисперсий в качестве критерия используется случайная величина, имеющая распределение —Стьюдента (Т) +Фишера – Снедекора (F) —нормальное (Z) — Пирсона
При статистической проверке гипотезы о равенстве генеральных средних, в случае, когда генеральные дисперсии известны, используется случайная величина, имеющая распределение — Фишера – Снедекора (F) + нормальное(Z) — Стьюдента(Т) — Пирсона
При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия известна) в качестве критерия используется случайная величина, имеющая распределение +Стьюдента (Т) — нормальное (Z) — Фишера – Снедекора (F) — Пирсона
При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия неизвестна) в качестве критерия используется случайная величина, имеющая распределение + нормальное (Z) —Фишера – Снедекора (F) — Пирсона —Стьюдента (Т)
При статистической проверке гипотезы о равенстве генеральных средних (генеральные дисперсии неизвестны, но равны) в качестве критерия используется случайная величина, имеющая распределение —Пирсона — нормальное (Z) + Стьюдента (Т) — Фишера – Снедекора (F)
ТЕМА 6. Корреляционно - регрессионный анализ
Уравнение регрессии отыскивается —выборочным методом —методом интегрированием по частям + методом наименьших квадратов —методом множителей Лагранжа
Корреляционной зависимостью называется статистическая зависимость, при которой каждому значению случайной величины Х ставится в соответствие —определенное значение случайной величины Y —распределение случайной величины Y —корреляционное отношение +числовая характеристика случайной величины Y
Коэффициент а в уравнении регрессии —тесноту связи между факторным и результативным признаками +на сколько единиц изменится значение результативного признака при изменении факторного признака на 1 единицу —на сколько процентов изменится значение результативного признака —изменение факторного признака
Если при равномерном возрастании значений факторного признака средние значения результативного признака равномерно возрастают, то уравнение регрессии обыскивается в виде +линейного уравнения —уравнения гиперболы — уравнения параболы —уравнения третьей степени
Если при равномерном возрастании значений факторного признака средние значения результативного признака неравномерно убывают, то уравнение регрессии отыскивается в виде —линейного уравнения +уравнения гиперболы — уравнения параболы —уравнение третьей степени
Универсальным показателем тесноты связи между факторным и результативным признаками является —уравнение регрессии +корреляционное отношение —факторная дисперсия результативного признака —остаточная дисперсия результативного признака
Корреляционное отношение отыскивается по формуле + —
— —
Cвязь между факторным и результативным признаками является тесной, если — — + —
Линейный коэффициент корреляции определяется формулой — —
— +
В случае линейного уравнения регрессии связь между факторным и результативным признаками является тесной, если + — — —
Общая дисперсия результативного признака – это мера колеблемости результативного признака под воздействием —только факторного признака — только случайных факторов +всех факторов, влияющих на изменение результативного признака —общего признака
Остаточная дисперсия результативного признака – это мера колеблемости признака под воздействием — олько факторного признака +только случайных факторов —всех факторов, влияющих на изменение результативного признака —общего признака
Cтатистической называется зависимость, при которой каждому значению случайной величины Х соответствует —определенное значение случайной величины Y —произвольное значение случайной величины Y +распределение случайной величиныY —постоянная величина величина Y
Корреляционная зависимость называется регрессионной, если каждому значению случайной величины X соответствует +средняя величина распределения случайной величины Y —дисперсия случайной величины Y — среднее квадратическое отклонение случайной величины Y —определенное значение случайной величины Y
Парная корреляция – это зависимость, при которой результативный признак Y зависит от —двух факторных признаков —множества факторных признаков — совокупности пар +одного факторного признака Х
Задачей регрессионного анализа является +определение формы связи между факторным и результативным признаками —установление тесноты связи между факторным и результативным признаками —вычисление ошибки показателя тесноты связи —определение доверительного интервала для показателя тесноты связи
Если связь между факторным признаком и средним значением результативного признака – линейная, то — — — +
Линейный коэффициент корреляции определяет тесноту связи между признаками Х и Y, если связь +линейная —дробно – линейная —гиперболическая — квадратичная
Корреляционная связь тем теснее, чем меньше рассеяние между результативным Y и факторным Х признаками под влиянием —учтенных факторов + неучтенных факторов —всех факторов —изучаемого факторного признака
Если влияние фактора Х мало осложняет действием других факторов, то зависимость между Y и Х является —слабой —случайной +тесной —остаточной
Отысканиезависимости по наблюдаемым значениям +выравниванием эмпирических данных —выпрямлением эмпирических данных — осреднением эмпирических данных —рассеянием эмпирических данных
СВогласно методу наименьших квадратов наилучшей аппроксимирующей кривой будет та, для которой —среднее отклонение ординат эмпирических точек от выравненных будет минимальным —квадрат среднего отклонения ординат эмпирических точек от выравненных будет минимальным —сумма отклонений ординат эмпирических точек от выравненных будет минимальной + сумма квадратов отклонений ординат эмпирических точек от выравненных будет минимальной
Уравнение, связывающее условную среднюю + уравнением регрессии —уравнением тесноты связи —гипотетическим уравнением —корреляционным уравнением
Корреляционном полем переменных (х,у) называется —совокупность точек (хi,уi) + изображение совокупности точек (хi,уi) на координатной плоскости —изображение линий, на которой обозначены точки (хi,уi) —таблица, в которой даны значения (
Теснота связи это —отношение суммы значений — производная Y по X +мера рассеяния результативного признака Y около линии регрессии —мера рассеяния факторного признака Х около уравнения регрессии
Значения линейного коэффициента корреляции принадлежат промежутку — — — +
Значения корреляционного отношения принадлежат промежутку — + — —
Множественная корреляция это зависимость —когда одному значению +зависимость результативного признака от двух и более факторных признаков —совокупность пар (хi,уi) —криволинейная зависимость между X и Y
Корреляционный анализ определяет —форму связи между X и Y —производную +тесноту связи между X и Y —
Линия, построения по наблюдаемым значениям — теоретической —выравнивающей +эмпирической —наблюдаемой
Система уравнений для определения коэффициентов уравнения регрессии называется системой —параметрических уравнений —нелинейных уравнений — функциональных уравнений +нормальныхъ уравнений
Корреляционный метод может быть применен, если число наблюдений — мало +достаточно велико —равно 5 —равно числу наблюдаемых значений
Определение тесноты связи между факторным Х и результативным Y признаками – это задача —регрессионного анализа —выборочного метода +корреляционного анализа —метода наименьших квадратов
Уравнение регрессии связывает значения факторного признака — определенным значением результативного признака —максимальным значением результативного признака +средним значением результативного признака —дисперсией результативного признака
Линия, построенная по уравнению регрессии, называется —эмпирической — наблюдаемой —выпрямляющей +выравнивающей
В уравнении регрессии — — + —
Дисперсия факторного признака — + — —
Зависимость средней выработки одного рабочего за смену Y(шт) от квалификации Х (разряды) приведена в таблице:
Уравнение регрессии —2,8 —5,3 +6,4 —7,2
Зависимость спроса на данный товар Y (тыс. шт.) от средних доходов населения Х (тыс. руб.) приведена в таблице:
Уравнение регрессии —1,2 —2,6 —4,4 +5,8
Зависимость среднего прироста объема выпускаемой продукции Y (тыс. шт.) от капиталовложений Х (млн.руб.) приведена в таблице:
Уравнение регрессии —1,9 —2,3 —3,2 +1,4
Тема 7. Типы задач математического программирования. Экономико-математические модели задач линейного программирования. Геометрическая интерпретация ЗЛП.
К задачам оптимизации относятся задачи на отыскание —целевой функции + максимума или минимума целевой функции —решения системы уравнений — решения системы неравенств
Критерием оптимальности задачи математического программирования является +целевая функция —система уравнений —система неравенств —условие неотрицательности переменных
Общая задача линейного программирования имеет вид — — —
+
Задача математического программирования является задачей линейного программирования, если —целевая функция является линейной, а система ограничений нелинейная —система ограничений – это система линейных уравнений или неравенств, а целевая функция нелинейная +целевая функция является линейной, а система ограничений – система линейных уравнений или неравенств —условие неотрицательности переменных - линейно
Задача математического программирования является задачей нелинейного программирования, если —условие неотрицательности переменных нелинейно + целевая функция является нелинейной —целевая функция является линейной — условие неотрицательности переменных не выполняется
Задача нелинейного программирования называется квадратичной, если — — + —
Задача нелинейного программирования называется задачей дробно – линейного программирования, если — — — +
Задача математического программирования называется задачей целочисленного программирования, если —все коэффициенты целевой функции – целые числа —все коэффициенты системы ограничений – целые числа —все +все
Абстрактное отображение реального экономического процесса с помощью математических выражений, уравнений, неравенств – это —система ограничений — целевая функция +экономико–математическая модель —условие неотрицательных переменных
Любая экономико – математическая модель задачи линейного программирования состоит из —целевой функции и системы ограничений +целевой функции, системы ограничений и условия неотрицательности переменных —системы ограничений и условия неотрицательности переменных — целевой функции и условия неотрицательности переменных
Задача математического программирования называется задачей сепарабельного программирования, если целевая функция + — — —
Оптимальное решение задачи математического программирования – это — допустимое решение системы ограничений —любое решение системы ограничений +допустимое решение системы ограничений, приводящее к максимуму или минимуму целевой функции —максимальное или минимальное решение системы ограничений
Если целевая функция —линейного программирования — целочисленного программирования —дробно – линейного программирования +квадратичного программирования
Динамическое программирование – это математический аппарат, позволяющий + осуществить оптимальное планирование многошаговых управляемых процессов —исследовать динамику функции —оказывать влияние на развитие процесса —наблюдать процесс в его развитии
Если целевая функция —линейного программирования — квадратичного программирования +дробно – линейного программирования — дробно – квадратичного программирования
Все ограничения в задаче математического программирования должны быть — одинакового смысла —противоречивы +непротиворечивы —противоположного смысла
Задачи линейного программирования предполагают —минимальные ресурсы — максимальные ресурсы —неограниченные ресурсы +ограниченные ресурсы
В задаче об оптимальном распределении ресурсов критерием оптимальности является +максимальная прибыль —минимальная прибыль —максимальные издержки —минимальные издержки
В задаче «о диете» критерием оптимальности является —максимальная прибыль — минимальная прибыль —максимальная стоимость рациона питания +минимальная стоимость рациона питания
Задачи об оптимальном распределении ресурсов и «о диете» относятся к задачам +линейного программирования —нелинейного программирования — динамического программирования —целочисленного программирования
Система ограничений называется стандартной, если она содержит все знаки —³ +£ —= —¹
Задача линейного программирования решается графическим способом, если в задаче —одна переменная +две переменные —три переменные —четыре переменные
Неравенство вида —прямую —окружность +полуплоскость —плоскость
Областью допустимых решений ЗЛП является —вся плоскость —круг +выпуклый многоугольник —координатные оси
Максимум или минимум целевой функции находится —в начале координат —на сторонах выпуклого многоугольника решений —внутри выпуклого многоугольника решений +в вершинах выпуклого многоугольника решений
Каноничкеским видом ЗЛП называется такой ее вид, в котором система ограничений содержит знаки —³ — £ += —¹
Для приведения ЗЛП к каноническому виду вводятся +дополнительные переменные —искусственные переменные —отрицательные переменные —нулевые переменные
Если ограничение задано со знаком «³», то дополнительная переменная вводится в это ограничение с коэффициентом —+1 +-1 —0 —М
Если ограничение задано со знаком «£», то дополнительная переменная вводится в это ограничение с коэффициентом ++1 —-1 —0 —М
В целевую функцию дополнительные переменные вводятся с коэффициентами — +1 —-1 +0 —M
В задаче об оптимальном распределении ресурсов дополнительная переменная —прибыль от реализации продукции i –го вида —прибыль от реализации 1 единицы продукции i – го вида —использованные ресурсы i – го вида +неиспользованные ресурсы i –го вида
В задаче об оптимальном распределении ресурсов коэффициент —прибыль от реализации продукции j – го вида + прибыль от реализации 1 единицы продукции j– го вида —количество продукции j – го вида —расход сырья для производства продукции j – го вида
В задаче об оптимальном распределении ресурсов переменная —прибыль от реализации продукции j – го вида — прибыль от реализации 1 единицы продукции j– го вида +количество продукции j – го вида —расход сырья для производства продукции j – го вида
В задаче «о диете» коэффициент +цена 1 единицы продукта j– го вида — расход продукта j – го вида — прибыль от использования продукта j– го вида — прибыль от реализации продукта j– го вида
В задаче «о диете» коэффициент +содержание питательного вещества с номером i в 1 единице j – го продукта —цена 1 единицы продукта j– го вида —количество j – го продукта, необходимого i – му животному —издержки на приобретение j – го продукта для прокорма i – го животного
В задаче об оптимальном распределении ресурсов коэффициент +количество ресурса с номером —неиспользованные ресурсы i - го вида —прибыль от реализации 1 единицы продукции j – го вида —количество продукции j – го вида
В задаче об оптимальном распределении ресурсов требование неотрицательности накладывается на —только основные переменные +на основные и дополнительные переменные —только на дополнительные переменные —первую и вторую переменные
В задаче о «диете» область допустимых решений —ограничена —незамкнута +неограничена —невыпукла
Динамическое программирование основано на решении —вероятностного уравнения —дифференциально
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 2254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.35.129 (0.01 с.) |

 называется
называется принимается
принимается

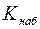
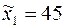 ;
;  . При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак




 ;
;  . При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак . При проверке гипотезы о равенстве выборочной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве выборочной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак . При проверке гипотезы о равенстве выборочной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве выборочной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак
 ) используется случайная величина, имеющая распределение
) используется случайная величина, имеющая распределение ) используется случайная величина, имеющая распределение
) используется случайная величина, имеющая распределение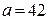 . По данным выборки размер
. По данным выборки размер 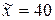 . При проверке гипотезы о равенстве генеральной средней стандарту в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральной средней стандарту в конкурирующей гипотезе должен быть знак о работе двух станков, то
о работе двух станков, то , то критическая область
, то критическая область , то критическая область
, то критическая область , то критическая область
, то критическая область , то критическая область
, то критическая область



 о работе двух станков, то
о работе двух станков, то о весе детали, то
о весе детали, то







 показывает
показывает




















 и
и  называется
называется со значением факторного признака
со значением факторного признака  , называется
, называется )
)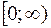



 соответствует множество значений
соответствует множество значений 

 коэффициент а равен
коэффициент а равен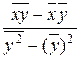



 равна
равна



 (max или min),
(max или min),  ,
, 







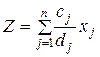


 - целые числа
- целые числа - целые числа,
- целые числа, 
 равна
равна

 , где
, где 

 ,то задача математического программирования является задачей
,то задача математического программирования является задачей описывает
описывает имеет экономический смысл:
имеет экономический смысл: целевой функции
целевой функции  - это
- это - это
- это , необходимого для изготовления 1 единицы продукции j – го вида
, необходимого для изготовления 1 единицы продукции j – го вида


