
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Случайные величины. Числовые характеристики случайных величин. Повторные независимые испытания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математическое ожидание случайной величины (с X+Y),где + — — —
Дисперсия случайной величины (с X+Y),где — + — —
Дисперсия разности двухнезависимых случайных величин X и Y равна — —0 + —
Математическое ожидание произведения двух независимых случайных величин X и Y равно — — — +
Индикатором события А называется случайная величина, которая —равна константе а> 1 —равна константе а <-1 —всегда равна 1 +равна 1, если в результате испытания событие А происходит и равна 0, если событие А не происходит
Законом распределения дискретной случайной величины называется соответствие между —возможными значениями случайной величины и рядом натуральных чисел + возможными значениями случайной величины и вероятностями их появления —математическим ожиданием случайной величины и ее средне – квадратическим отклонением —возможными значениями случайной величины и ее математическим ожиданием
Сумма всех вероятностей значений дискретной случайной величины равна —0 — +1 —-1
Математическое ожидание дискретной случайной величины вычисляется по формуле — — — +
Математическое ожидание постоянной величины С равна +С —1 —0 — не определено
Математическое ожидание случайной величины (с X-Y),где + — — — —
Дисперсия дискретной случайной величины определяется по формуле — + — —
Дисперсия постоянной величины С равна —1 —C +0 —не определена
Среднее квадратическое отклонение — — + —M(X)
Функцией распределения случайной величины Х называют функцию F (x), равную — — + —
Если F (x) – функция распределения случайной величины Х, — — — +
Если F (x) – функция распределения случайной величины Х, то плотность распределения равна — F (x) —- F (x) — +
Дисперсия + — — —
Из следствия из интегральной теоремы Лапласа следует что —относительная частота наступлений события равна вероятности появления этого события —относительная частота наступлений события отклонится от вероятности появления этого события —с увеличением числа n независимых испытаний вероятность наступления события увеличивается +с увеличением числа испытаний n относительная частота
Вероятность появления события А m раз в n повторных независимых испытаниях при — + — —
Вероятность + — —
—
Математическое ожидание случайной величины – числа появлений события А в n независимых испытаниях с вероятностью p наступления события А – равно — — — +
Дисперсия случайной величины – числа появлений события А в n независимых испытаниях с вероятностью p наступления события А – равна + — — p —
Дискретная случайная величина распределяется по биномиальному закону распределения, если она выражает —вероятность появления события А в каждом испытании —число появлений события А в n различных испытаниях + число появлений события А в n независимых испытаниях, проводимых в одинаковых условиях и с одинаковой вероятностью появления события в каждом испытании —число появлений события А в n независимых испытаниях, проводимых в одинаковых условиях, вероятностью i – м испытании
Вероятность появления события А m раз в n независимых испытаниях —зависит только от m и n +зависит от m, n и p —зависит только от m —не зависит от m и n
Повторными независимыми испытаниями относительно события А называются испытания —которые повторяются —которые повторяются и не зависят от других испытаний +которые проводятся в одних и тех же условиях и с одинаковой вероятностью появления события А в каждом испытании — в которых событие А повторяется
Вероятность появления события А m раз в n повторных независимых испытаниях при +формулой Бернулли —локальной теоремой Лапласа —интегральной теоремой Лапласа —формулой Пуассона
Наивероятнейшим числом наступлений события А в n независимых испытаниях называется —наибольшее число наступлений события А —наибольшая вероятность наступления события А —число наступлений события А при наибольшем числе испытаний + число наступлений события А, при котором вероятность наступления события А в n независимых испытаниях наибольшая
Функция —четная возрастающая —нечетная убывающая +четная положительная —нечетная положительная
Функция + нечетная возрастающая —четная возрастающая —нечетная убывающая — четная убывающая
Локальная теорема Лапласа позволяет вычислить —наивероятнейшее число наступлений события в n независимых испытаниях —относительную частоту наступлений события в n независимых испытаниях +вероятность появления события m раз в n независимых испытаниях (n >10) —вероятность отклонения числа появлений события m от числа независимых испытаний n
Интегральная теорема Лапласа позволяет вычислить —вероятность появления события A m раз в n испытаниях (n >10) + вероятность появления события A в n испытаниях не менее а, но не более —наивероятнейшее число появлений события A в n независимых испытаниях (n >10) —относительную частоту наступлений события A в n независимых испытаниях
Выражение —дисперсией дискретной случайной величины — вариацией дискретной случайной величины +математическим ожиданием дискретной случайной величины —средним квадратическим отклонением
Выражение —дисперсией случайной величины х — вариацией случайной величины х — математическим ожиданием случайной величины х + средним квадратическим отклонением
Вероятность появления события А m раз в n повторных независимых испытаниях определяется формулой Бернулли при — — — +
Для случайной величины – числа появлений события А в n независимых испытаниях с вероятностью p наступления события А выражение np является — дисперсией —вариацией +математическим ожиданием —средним квадратическим отклонением
Если +1 —3 —5 —7
Если —1 +5 —13 —16
Если —1 —3 +5 —9
Если —1 —3 +5 —17
Указать неверное значение дисперсии +-1 —4 —9 —16
Указать верное значение дисперсии —-9 —-4 +1 —-1
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.180.253 (0.007 с.) |

 ,
,  - независимые случайные величины, равно
- независимые случайные величины, равно








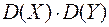




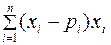









 случайной величины Х равно
случайной величины Х равно


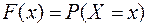



 – некоторые числа, то
– некоторые числа, то  равна
равна
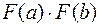

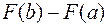


 , определяется формулой
, определяется формулой

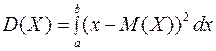

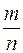 приближается к вероятности появления события в одном испытании
приближается к вероятности появления события в одном испытании определяется формулой
определяется формулой



 появления события А в n повторных независимых испытаниях (n >10) равна
появления события А в n повторных независимых испытаниях (n >10) равна









 появления события А в
появления события А в определяется
определяется обладает следующими свойствами
обладает следующими свойствами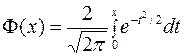 обладает следующими свойствами
обладает следующими свойствами раз (n >10)
раз (n >10)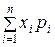 является
является является
является


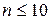
 , а
, а  , то дисперсия случайной величины равна
, то дисперсия случайной величины равна , а
, а  , то
, то 
 , а
, а  , то
, то 
 ; а
; а  , то
, то 



