
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики дискретных случайных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Как известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание, которое приближенно равно среднему значению случайной величины. o Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то Если случайная величина Х принимает счетное число значений, то Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная). Пример 1. Найти математическое ожидание случайной величины Х, зная ее ряд распределения.
Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р. Случайная величина Х—число появлений события А в одном испытании, может принимать значения х1=1 (событие А наступило) с вероятностью р и х2=0 (А не наступило) с вероятностью q=1-p.
Таким образом, математическое ожидание числа появлений события в одном испытании равно вероятности это события. Свойства математического ожидания: Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: M(C)=C. Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно, Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х. Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X). Если случайная величин Х имеет ряд распределения
Ряд распределения случайной величины СХ
Математическое ожидание случайной величины СХ o Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn Если взять B1=]-∞, x1[; B2=]-∞, x2[; …; Bn=]-∞,xn[, то
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий. Свойство 4. Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых. Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей. Обозначим случайную величину Х—число очков, выпавших на первой кости, через Y обозначим число очков, выпавших на второй кости. Возможные значения этих величин одинаковы и равны 1,2,3,4,5,6, причем вероятность каждого из этих значений равна
Теорема 1. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события
Согласно примеру 2 o Дисперсией случайной величины называется число o Средним квадратическим отклонением случайной величины Х называется число
Пример 4. Найти дисперсию случайной величины Х, которая задана рядом распределения.
Ряд распределения случайной величины Х2
Свойства дисперсии. Свойство 1. Дисперсия постоянной величины С равна 0.DC=0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин. Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: Случайная величина Х—число появлений события А в n независимых испытаниях.
Пример. Проводятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X—числа появлений события в этих испытаниях. n=10; p=0,6; q=0,4.
o Начальным моментом порядка к случайным величинам Х называют математическое ожидание случайной величины Хk:
Пользуясь этими моментами, формулу для вычисления дисперсии Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонения Х-ХМ. o Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х-МХ)k.
Исходя из определения центрального момента и пользуясь свойствами математического ожидания, можно получить формулы:
Моменты более высоких порядков применяются редко. Замечание. Моменты, определенные выше, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 679; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 .
. , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. .
. .
. .
. .
. .
. .
. —совместимая функция распределения случайных величин Х1,Х2,…,Хn. Таким образом,
—совместимая функция распределения случайных величин Х1,Х2,…,Хn. Таким образом,  . Данное равенство также можно взять в качестве определения независимости случайных величин.
. Данное равенство также можно взять в качестве определения независимости случайных величин.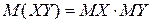 .
. .
.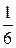 . Найдем математическое ожидание числа очков, которые могут выпасть на первой кости.
. Найдем математическое ожидание числа очков, которые могут выпасть на первой кости. . Очевидно, что
. Очевидно, что  .
. .
.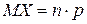 .
. . По свойству 4:
. По свойству 4: .
. . Таким образом, получим
. Таким образом, получим  . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания. .
.
 .
.
 .
. .
. .
.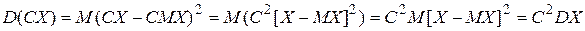 .
. .
.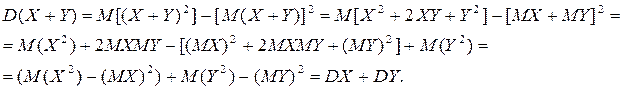
 .
. .
. . Т.к. MX1=p.
. Т.к. MX1=p.  , то
, то  . Очевидно, что дисперсия остальных случайных величин также равна pq, откуда
. Очевидно, что дисперсия остальных случайных величин также равна pq, откуда  .
. . В частности,
. В частности,  ,
,  .
. можно записать так:
можно записать так:  .
. . В частности
. В частности ,
,  . Следовательно,
. Следовательно, 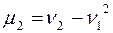 .
. .
. .
.


