
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная совокупность. ВыборкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали. Иногда проводят сплошное обследование, т.е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование нет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. О. Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. О. Генеральной совокупностью называется совокупность объектов, из которых производится выборка. О. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100. Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако, если это число достаточно велико, то иногда в целях упрощения вычислений или для облегчения теоретических выводов, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки. Для того чтобы по данным выборки можно было достаточно уверено судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируется так: выборка должна быть репрезентативной (представительной). В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Предположим, что можем производить измерения случайной величины Х. Допустим, что в n экспериментах результаты измерений Предполагаем, что выполняются следующие две предпосылки: 1. Эксперименты проводятся в одинаковых условиях; 2. Эксперимента проводятся независимо друг от друга. О. Говорят, что результаты n экспериментов Пусть требуется произвести измерения случайных величин
… …. ….
… … … … Тогда случайные величины Если Из первой предпосылки следует, что Из второй предпосылки следует, что О. Говорят, что случайные величины О. Функция распределения F(x) случайной величины Х называется теоретической функцией распределения или функцией распределения генеральной совокупности. Как абстрактную, так и конкретную выборку будем обозначать одними и теми же буквами При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные. О. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. О. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. На практике обычно пользуются бесповторным случайным отбором. На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида: 1. Отбор не требующий разбиения (расчленения) генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор. 2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор; б) механический отбор; в) серийный отбор. О. Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различными способами. Например, для извлечения n объектов из генеральной совокупности объема N поступают так: выписывают номера от 1 до N на карточках, которые тщательно перемешивают, и наугад вынимают карточку; объект, имеющий номер, указанный на карточке, подвергают обследованию. Затем карточки перемешивают, наугад вынимают одну из них и т.д. Так поступают n раз. В итоге получают простую случайную повторную выборку объема n. Если извлеченные карточки не возвращать в пачку, то выборка является простой случайной бесповторной. При большом объеме генеральной совокупности описанный процесс является очень трудоемким. В этом случае пользуются готовыми таблицами “случайных чисел”, в которых числа расположены в случайном порядке. О. Типическим называют отбор, при котором объекты выбираются не из всей генеральной совокупности, а из каждой ее “типической” части. Например, если детали изготовлены на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если продукция изготовлена на нескольких станках, среди которых есть более и менее изношенные, то в данном случае типический отбор целесообразен. О. Механическим называют отбор, при котором генеральную совокупность “механически” делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20% изготовленных деталей, то отбирают каждую пятую деталь. Замечание: Необходимо отметить, что иногда механический отбор может не обеспечить репрезентативность выборки. Например, если замена резца в станке проводится сразу после отбора каждой двадцатой детали, то обратными окажутся все детали, обточенные затупленными резцами. В таком случае можно устранить совпадение ритма отбора с ритмом замены резца. О. Серийным называют отбор, при котором объекты отбираются из генеральной совокупности не по одному, а “сериями”, которые подвергаются сплошному обследованию. Например, если изделия изготовлены большой группой станков, то подвергают сплошному обследованию только продукцию нескольких станков. Серийным отборам пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно. На практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы. Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором отбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.
3. Эмпирическая функция распределения. Предположим, что имеется выборка Через Y обозначим случайную величину с рядом распределения (законом распределения)
О. Случайная величина Y называется выборочной или эмпирической. Ряд распределения случайной величины Y называется выборочным или эмпирическим. О. Числовые характеристики теоретической СВ Х называются генеральными характеристиками. О. Числовые характеристики эмпирической случайной величины Y называются выборочными. О. Генеральным начальным элементом к-го порядка называется число bk=MXk. О. Выборочным начальным моментом к-го порядка называется число О. Выборочной средней называется среднее арифметическое выборочного ряда распределения, т.е. О. Генеральным центральным моментом к-го порядка называется число mk=M(X-MX)k О. Выборочным центральным моментом к-го порядка называется число
В частности,
О. Эмпирической функцией распределения называется функция распределения выборочной (эмпирической) случайной величины Y. Обозначается эта функция:
О. Последовательность значений Пусть из генеральной совокупности извлечена выборка, причем О. Наблюдаемые значения Числа наблюдений О. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот попавших в этот интервал вариант). Замечание В теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями. В МС – соответствие между наблюдаемыми вариантами и их частотами или относительными частотам. Пример 1 Задано распределение частот выборки объема
Написать распределение относительных частот. Решение Найдем относительные частоты, для чего разделим частоты на объем выборки:
Напишем распределение относительных частот:
Контроль: Пусть имеется вариационный ряд
Если n велико, то Таким образом, эмпирическая функция распределения служит для оценки функции распределения генеральной совокупности. Пример 2 Построить эмпирическую функцию распределения по данному распределению выборки:
Решение Найдем объем выборки 12+18+30=60. Наименьшая варианта равна 2, следовательно:
Значение
Значение
Так как x=10 – наибольшая варианта, то
Искомая эмпирическая функция:
График этой функции:
Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму. О. Полигоном частот называют ломаную, отрезки которой соединяют точки
О. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки
Предположим, что Интервал, в котором заключены все наблюдаемые значения, разбиваем на k частичных интервалов длины
Полученная ступенчатая фигура называется гистограммой относительных частот.
О. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной Площадь
|
||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 994; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 - некоторые числа.
- некоторые числа. . Если производить измерения сериями, то результаты можно записать следующим образом:
. Если производить измерения сериями, то результаты можно записать следующим образом: - 1 серия;
- 1 серия; - 2 серия;
- 2 серия;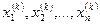 - к-ая серия;
- к-ая серия; , то можно представить себе бесконечную генеральную совокупность. Тогда Х – непрерывная СВ.
, то можно представить себе бесконечную генеральную совокупность. Тогда Х – непрерывная СВ.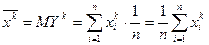 .
. .
.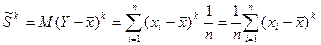 .
. - выборочная дисперсия
- выборочная дисперсия - оценка генеральной дисперсии
- оценка генеральной дисперсии 
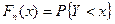 .
.
 , где
, где  - число выборочных значений
- число выборочных значений 



 , записанных в возрастающем порядке
, записанных в возрастающем порядке 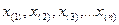 где
где  называется вариационным рядом выборки.
называется вариационным рядом выборки. наблюдалось
наблюдалось  раз,
раз,  раз, …,
раз, …,  раз и
раз и  - объем выборки.
- объем выборки. называют вариантами.
называют вариантами.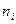 называют частотами, а их отношения к объему выборки
называют частотами, а их отношения к объему выборки  - относительными частотами.
- относительными частотами. :
:





 , где F(x) – функция распределения генеральной совокупности.
, где F(x) – функция распределения генеральной совокупности.

 при
при  .
. наблюдалось 12 раз, следовательно
наблюдалось 12 раз, следовательно при
при 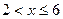 .
. , а именно
, а именно 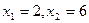 наблюдалось 12+18=30 раз, следовательно,
наблюдалось 12+18=30 раз, следовательно, при
при  .
. при
при 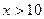 .
.

 Для построения полигона частот на оси абсцисс откладывают варианты
Для построения полигона частот на оси абсцисс откладывают варианты  соединяют отрезками и получают полигон частот.
соединяют отрезками и получают полигон частот.
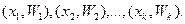

 . Необходимо построить оценку плотности
. Необходимо построить оценку плотности  , где
, где 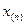 - наибольшая, а
- наибольшая, а  - наименьшая из вариант,
- наименьшая из вариант, , где
, где 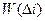 - число выборочных значений, попадающих в i – й интервал
- число выборочных значений, попадающих в i – й интервал  , n – объем выборки.
, n – объем выборки.

 (вместо
(вместо  )
) , т.е. равна сумме всех частот, т.е. объему выборки.
, т.е. равна сумме всех частот, т.е. объему выборки.


