
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точечные оценки неизвестных параметровСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предположим, что имеется выборка О1. Оценкой или статистикой параметра О2. Оценка О3. Оценка О4. Несмещенная оценка ┐ Пример: Предположим, что имеется выборка В качестве оценки 1. Вывод: 2. Поскольку По определению 3 3. Эффективность оценки зависит от закона распределения генеральной совокупности. Оценка 1. Следовательно,
Следовательно,
Следовательно, 2. Можно проверить, что
5. Методы получения оценок. Пусть
Более того, можно рассматривать Поскольку
Тогда
Таким образом,
Следовательно, 1. При любом фиксированном 2. Проверим состоятельность оценки
если По теореме о двух милиционерах Т.о. 3. Оказывается, что эта оценка является также и эффективной. Метод моментов. Состоит в том, что выборочные (эмпирические) моменты принимаются за оценки соответствующих теоретических (генеральных) моментов и неизвестные параметры выражаются через эти моменты. Начальные моменты: 1. Теоретические (генеральные)
где 2. выборочные (эмпирические) Центральные моменты: 1. Теоретические (генеральные)
2. выборочные (эмпирические)
При Необходимо отметить, что теоретическая моменты – случайные величины, а эмпирические – фиксированные постоянные. Таким образом, для получения оценок неизвестных параметров
Здесь оценки параметров Пример1. Пусть имеется выборка
Найти оценки параметров
Метод максимального правдоподобия. Пусть
Фишер предложил находить оценки Те значения Введем функцию Для этого составляется система
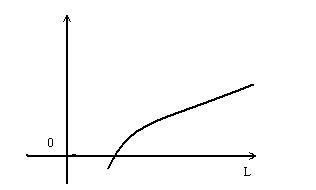
 (следовательно и (следовательно и  ) в максимум. При этом методе получаются состоятельные,но смещенные оценки. ) в максимум. При этом методе получаются состоятельные,но смещенные оценки.
Пример2. Имеется выборка
Составим систему:
|
||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 из генеральной совокупности, закон распределения которой зависит от неизвестного параметра
из генеральной совокупности, закон распределения которой зависит от неизвестного параметра  (например, функция распределения
(например, функция распределения  ).
). от выборочных значений
от выборочных значений  неизвестного параметра
неизвестного параметра  .
.
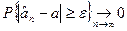 )
)  .
.
 несмещенная оценка параметра
несмещенная оценка параметра 
 ,
,  . Здесь
. Здесь  - генеральная дисперсия.
- генеральная дисперсия. . В качестве оценки
. В качестве оценки  . Проверим, насколько хороша оценка
. Проверим, насколько хороша оценка  :
:
 . По закону больших чисел в форме Чебышева
. По закону больших чисел в форме Чебышева 
 .
. .
. (1)
(1)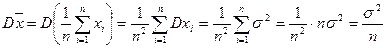 .
.
 (2)
(2)
 оценка
оценка  , тогда
, тогда
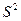 - несмещенная оценка и называется исправленной выборочной дисперсией.
- несмещенная оценка и называется исправленной выборочной дисперсией. - неисправленная выборочная дисперсия.
- неисправленная выборочная дисперсия. - исправленная выборочная дисперсия.
- исправленная выборочная дисперсия. , зависящей от
, зависящей от  неизвестных параметров. Необходимо найти оценки
неизвестных параметров. Необходимо найти оценки  параметров
параметров  .
. при больших
при больших  .
. как оценку
как оценку  при каждом фиксированном значении
при каждом фиксированном значении 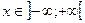 .
. , то в качестве успеха в случайном испытании примем:
, то в качестве успеха в случайном испытании примем: .
.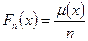 , где
, где  - число выборочных значений, меньших
- число выборочных значений, меньших  , т.е. число успехов.
, т.е. число успехов. , где
, где  ,
, .
. .
.

 т.к.
т.к. 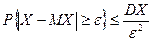 ,
, - конечно.
- конечно. .
.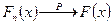 , т.е.
, т.е. 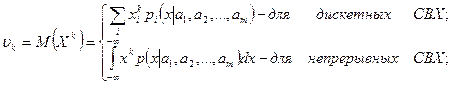
 - вероятность
- вероятность 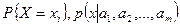 - плотность случайной величины X.
- плотность случайной величины X. .
.
 .
. .
.


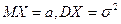 .
.



 , зависящую от
, зависящую от  (по критерию независимости непрерывных случайных величин)=
(по критерию независимости непрерывных случайных величин)=  .
.  - функция правдоподобия.
- функция правдоподобия. .
. - логарифмическую функцию правдоподобия. Надо решать задачу
- логарифмическую функцию правдоподобия. Надо решать задачу 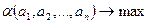 .
.
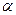
 ;
; ;
;
 .
.





