
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочные уравнения линейной регрессииСодержание книги
Поиск на нашем сайте
На практике, как правило, иметься только выборка. Например, ( Эмпирический коэффициент корреляции r является мерой тесноты линейной связи между двумя случайными величинами. С геометрической точки зрения это означает, что чем теснее располагаются точки на диаграмме рассеивания вокруг линии регрессии, тем выше абсолютная величина регрессии и наоборот. На рисунке 1-4 изображены несколько диаграмм рассеивания.
рис.1 рис.2
рис.3 рис.4
Диаграмма на рис.1 указывает на отрицательную функциональную связь (r=-1), на рис.2- на относительно высокую степень положительной корреляции (r≈0,8), на рис.3- умеренную степень отрицательной корреляции (r≈ -0,5), на рис.4 – отсутствие корреляции (r=0). По диаграмме рис.4 видно, что если коэффициент корреляции равен 0, то независимо от того, чему равна величина переменной X, оцениваемая величина зависимой переменной всегда равна Сначала, для построения диаграммы рассеивания строят корреляционное поле, т.е. наносят на плоскость все точки.
зависимости, начинают строить линейную регрессию.
рис.5
Если же точки расположены как на рис.6, то строят параболическую регрессию и уравнение вида параболы. Обозначим а=МХ, в=МУ, r= вместо них логично взять их оценки:
рис.6
cov(X,Y)=M[(X-MX)(Y-MY)]; cov(X,Y)≈ Подставляя в уравнение линейной регрессии оценки, получаем:
Метод наименьших квадратов.
Эти уравнения можно получить методом наименьших квадратов:
Метод наименьших квадратов или метод Гаусса сводиться к тому, что коэффициенты
Для этого составляется функция F( Берутся частные производные от F(
Составляется система из 2-х уравнений с 2-мя неизвестными, откуда и находятся
Дисперсионный анализ
Опр: Дисперсионным анализом называют статистический метод анализа результатов измерений, зависящих от различных одновременно действующих факторов. Ограничимся рассмотрением простейшего случая, когда действует один фактор. Пусть, например, выборка разбита на r групп, причем i-я группа содержит Нам нужно проверить гипотезу, согласно которой В физической постановке эта задача выглядит так: одна и та же величина a измеряется r различными приборами, имеющими одинаковую точность. Нас интересует, имеют ли приборы различные систематические ошибки. В рассматриваемом примере исследуется влияние одного фактора(прибора) на погрешность измерения. Введем следующие обозначения: Групповые средние Если все
в следующем виде: Равенство (2) следует из (1), если воспользоваться формулами:
Опр: Сумму По лемме Фишера величина Можно показать, что если
имеет распределение Фишера с r-1, n-r состояниями свободы. Величина (4) может быть использована для проверки гипотезы о равенстве математических ожиданий
и, следовательно, сумма
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 ),…,(
),…,( ).
).





 Если видят, что точки имеют тенденцию к линейной
Если видят, что точки имеют тенденцию к линейной
 =DX,
=DX,  =DY,
=DY,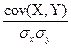 . Т.к. наши параметры неизвестны, то
. Т.к. наши параметры неизвестны, то ,
, 
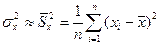 ;
;  ;
; .Коэффициент корреляции r=
.Коэффициент корреляции r= 
 -выборочное уравнение линейной регрессии Y на X.
-выборочное уравнение линейной регрессии Y на X.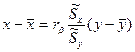 - выборочное уравнение линейной регрессии X на Y.
- выборочное уравнение линейной регрессии X на Y.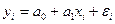 , где
, где  -некоторая ошибка измерений,
-некоторая ошибка измерений, 
 и
и  нужно искать из того, что сумма квадратов ошибок стремиться к минимуму, т.е.
нужно искать из того, что сумма квадратов ошибок стремиться к минимуму, т.е. →min по всем наблюдениям.
→min по всем наблюдениям. )=
)=  .
.




 Следовательно, получаем уравнение линейной регрессии Y на X:
Следовательно, получаем уравнение линейной регрессии Y на X: 
 величин
величин  Предположим, что все указанные величины распределены нормально и
Предположим, что все указанные величины распределены нормально и 
 , j=1,…,
, j=1,…,  .
.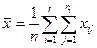 ,
,  , n=
, n= 
 являются несмещенными и состоятельными оценками величин
являются несмещенными и состоятельными оценками величин  .
. должен быть более значительным. Представим общую, или полную, сумму квадратов отклонений:
должен быть более значительным. Представим общую, или полную, сумму квадратов отклонений:  =
=  (1)
(1) (2), где
(2), где  =
= 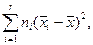
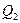 =
=  . (3)
. (3)
 , следовательно,
, следовательно, 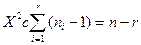 степенями свободы.
степенями свободы. , то
, то  . Следовательно, при
. Следовательно, при  величина
величина . (4)
. (4) . Если эта гипотеза верна, то
. Если эта гипотеза верна, то 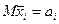 ,
, 
 , то гипотеза
, то гипотеза  отвергается. Здесь С определяется по таблице распределения Фишера с уровнем значимости
отвергается. Здесь С определяется по таблице распределения Фишера с уровнем значимости 



