
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство комплекснозначных случайных величин.Содержание книги
Поиск на нашем сайте
Если комлекснозначные случайные величины Z1 и Z2—независимы, то математическое ожидание их произведения равно произведению математических ожиданий, т.е.
0. 4 Характеристической функцией случайной величины Формулы для вычисления характеристической функции. Случай 1. Пусть
Случай 2. Пусть Пример 1. Пусть Пример 2. Пусть случайная величина
Если t=0, то Из примера 1, § 12 найдена производящая функция случайной величины
Пример 3. Пусть случайная величина
Если
Производящая функция
Таблица 1. Производящие функции.
Таблица 2. Характеристические функции.
Свойства характеристических функций. Свойство 1. Характеристическая функция определена для любой случайной величины. При этом
Поскольку Свойство 2. Характеристическая функция случайной величины
Свойство 3. Если случайные величины
Свойство 4. Если М Замечание. Необходимо отметить, что функция распределения величины однозначно определяется характеристической функцией. Таким образом, характеристическая функция является законом распределения случайной величины.
Законы больших чисел
0. 1 Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа
0. 2 Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство Чебышёва: Для
{x││x-MX│≥ε}
{x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε}
Таким образом,
Теорема 2. (закон больших чисел в форме Чебышёва). Пусть Х1,Х2,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е. Обозначим через
Отсюда Теорема 3. (Закон больших чисел в форме Бернулли). Пусть μ—число успехов в n независимых испытаниях Бернулли с вероятностью успеха р в одном испытании, тогда Введем случайные величины μi—число успехов в i-ом испытании. Тогда
μ1, μ2,…, μn—независимы. По закону больших чисел в форме Чебышёва
В чем смысл закона больших чисел в форме Бернулли? Пусть в результате эксперимента может произойти или не произойти событие А. P(A)—вероятность события А в одном эксперименте. Эксперимент повторяется N раз, N(A)—число появлений события А в этих N экспериментах.
Таким образом, закон больших чисел в форме Бернулли теоретически подтверждает устойчивость относительных частот, т.е. стабилизацию при большом числе испытаний относительной частоты вокруг вероятности (относительная частота ≈Р(А)).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 .
.
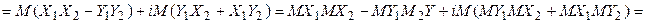
 .
. называется функция
называется функция  , где
, где  .
.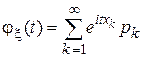 .
. . Тогда характеристическая функция
. Тогда характеристическая функция  .
. . Тогда характеристическая функция случайной величины
. Тогда характеристическая функция случайной величины  —производящая функция от аргумента
—производящая функция от аргумента  .
. . Найти характеристическую функцию
. Найти характеристическую функцию  .
.  , m=0,1,2…,n.
, m=0,1,2…,n. .
. .
. .
. , если
, если  . Найти характеристическую и производящую функции.
. Найти характеристическую и производящую функции. , m=0,1,2,…
, m=0,1,2,…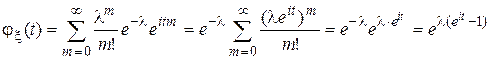 . t=0,
. t=0,  .
.

 , k=0,1,2,…
pqk
, k=0,1,2,…
pqk


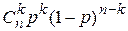 , k=0,1,2…,n.
, k=0,1,2…,n.

 , k=0,1,…
, k=0,1,…





 ,
, 

 ,
, 

 ,
, 



 ,
,  .
. .
. , то
, то 
 , где a, b—некоторые числа.
, где a, b—некоторые числа. .
. .
. —независимы, то характеристическая функция суммы данных случайных величин равна произведению характеристических функций этих случайных величин, т.е.
—независимы, то характеристическая функция суммы данных случайных величин равна произведению характеристических функций этих случайных величин, т.е. 
 .
. , характеристическая функция случайной величины
, характеристическая функция случайной величины 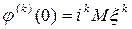 , где
, где  .
. , т.е.
, т.е. 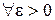
 при
при  . Обозначается
. Обозначается  .
. .
. .
.

 .
.
 .
. . Тогда эта последовательность удовлетворяет закону больших чисел.
. Тогда эта последовательность удовлетворяет закону больших чисел. . Нужно доказать, что
. Нужно доказать, что  .
. .
. (т.к.
(т.к. 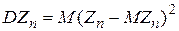 ).
). .
.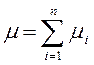 .
. ,
,  (т.к.
(т.к.  ).
). (т.е. дисперсия ограничена
(т.е. дисперсия ограничена  ).
). .
. .
. —относительная частота появления события А.
—относительная частота появления события А. . N(A)=μ,
. N(A)=μ,  .
.


