
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точечные оценки числовых характеристикСодержание книги
Поиск на нашем сайте
Введем понятия теоретического и эмпирического момента. Начальные теоретические моменты определяется следующим образом
Мы выделили плотность распределения
Если Допустим, известен закон распределения случайной величины. Однако параметры распределения неизвестны. Имеется случайная выборка из этой случайной величины, то-есть Так как полученные каждого измерения равновероятно, то эмпирический момент первого порядка оценивается с помощью следующей формулы:
Известно, что при увеличении объема выборки n (количество измерений), теоретическое и эмпирическое значения сходятся по вероятности, поэтому можно записать У нас получилось одно уравнение с двумя неизвестными. И решить его невозможно. Поэтому формируем начальный момент второго порядка.
…
Количество составленных таким образом уравнений, должно соответствовать количеству оцениваемых параметров. Решение системы уравнений обозначим следующим образом:
Кроме начальных моментов каждого порядка, для составления системы уравнений используются центральные моменты -ого порядка.
Центральный момент второго порядка называется дисперсия. Эмпирический центральный момент второго порядка:
Для оценки параметров нормального распределения, целесообразно использовать следующую систему уравнений:
Тогда решение будет математическое ожидание и дисперсия. Рассмотренный выше метод получили название метода момента. Этот методы был применен для оценки параметров нормального закона распределения. Решение этой системы уравнений дало следующие результаты.
Для нормального закона эти результаты получили специальное название
Метод максимального правдоподобия.
Исходные данные:
Целью обработки является, как и в предыдущем случае Наносим результаты измерений на оси абсцисс: … Придаем вектору
Проводим второй вектор. Лучше соответствует тот результат измерения закон распределения, у которого вероятность измерений больше. Самый лучший это тот который обеспечивает максимум этой вероятности.
Статистической оценкой вектора параметра
Это классическая задача исследования функции (правдоподобия) на экстремумы. В рамках этой задачи составляется следующая система уравнений:
Для нормального закона распределения статистические оценки закона Как уже указывалось ранее, статистическая оценка 1. Несмещённость 2. Состоятельность 3. Эффективность Результат оценки зависит от свойств анализируемых данных. Чаще всего эти методы оценки отличаются по эффективности. Кроме этих двух методов на практике используется: 1. Метод наименьших квадратов. 2. Метод наименьших абсолютных отклонений. 3. Метод наименьшего максимального абсолютного отклонения. 4. Каждый из этих методов имеет свою область применений. Базовым среди этих методов является метод максимального правдоподобия. Результат точечного оценивания широко используется в практике информационных управляющих систем. Они используются для адаптивного управления (Теория управления), для идентификации объекта (Система искусственного интеллекта), техника обработки сигналов и изображений.
Второй модуль (?) 01.01.12 Регрессионный анализ
…(график)…
Мы сделали статистическую оценку функции регрессии, полученную по выборке объему m.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.123.149 (0.007 с.) |

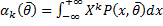
 – вектор числовых характеристик распределения.
– вектор числовых характеристик распределения.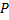 – плотность вероятностей.
– плотность вероятностей.
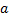 – математическое ожидание.
– математическое ожидание. равно единицы, то это формула математического ожидания. Математическое ожидание является начальным моментом первого порядка.
равно единицы, то это формула математического ожидания. Математическое ожидание является начальным моментом первого порядка. конкретных измерений -
конкретных измерений -  ,
,  ,…,
,…,  . Целью обработки является статистическая оценка вектора параметров
. Целью обработки является статистическая оценка вектора параметров 



 – статистическая оценка параметров
– статистическая оценка параметров  полученная по случайной выборке
полученная по случайной выборке 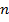 .
. (функция)
(функция)
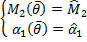


 – средне выборочное.
– средне выборочное. – выборочная дисперсия.
– выборочная дисперсия.
 - имеется
- имеется  значение наобум и рисуем на графике.
значение наобум и рисуем на графике. – это вероятность того, что измерения
– это вероятность того, что измерения  относятся к закону распределения
относятся к закону распределения 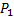 .
. – вероятность того, что все пять измерений относятся к закону распределения 1.
– вероятность того, что все пять измерений относятся к закону распределения 1. - функция правдоподобия.
- функция правдоподобия. – это аргумент функции правдоподобия, при котором она достигает максимума.
– это аргумент функции правдоподобия, при котором она достигает максимума.
 выборка, состоящая из n единиц, которая имеет два значения X и Y. Полученное значение роста мы упорядочиваем в порядке возрастания
выборка, состоящая из n единиц, которая имеет два значения X и Y. Полученное значение роста мы упорядочиваем в порядке возрастания  . Начинаем обрабатывать данные для значения роста
. Начинаем обрабатывать данные для значения роста  (студенты минимального роста). Получаем значение весов студентов с ростом
(студенты минимального роста). Получаем значение весов студентов с ростом 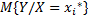 - условное математическое ожидания случайной величины Y (вес), при котором случайное значение X (рост) имеет значение
- условное математическое ожидания случайной величины Y (вес), при котором случайное значение X (рост) имеет значение  .
. – полученную функцию назовем функцией регрессии случайной величины Y на случайную величину X.
– полученную функцию назовем функцией регрессии случайной величины Y на случайную величину X. - условное математическое ожидания случайной величины X (рост), при котором случайное значение Y (вес) имеет значение
- условное математическое ожидания случайной величины X (рост), при котором случайное значение Y (вес) имеет значение  .
.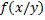 – функции регрессии веса на рост.
– функции регрессии веса на рост.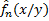 – статистическая оценка функции регрессии на рост по выборке объема n.
– статистическая оценка функции регрессии на рост по выборке объема n.


