
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Представление информации»Содержание книги
Поиск на нашем сайте
6.09.2012 Тема: «Представление информации» Любое практическое исследование на начальном этапе включает стадию сбора информации. Для изучения предмета или объекта необходимо систематизировать данные. Для обобщения необходимо выделять совокупности общих или различных свойств объектов. Такие свойства называются признаками. Признаки бывают: 1. Детерминированные 2. Логические 3. Вероятностные 4. Структурные Одним из универсальных представлений является табличное. Чтобы извлечь информацию необходимо представить данные в виде модели. Модель – абстрактное представление данных с целью улучшения интерпретации. Виды моделей: · Математическая · Физическая · Информационная Классификация моделей: 1. Гипотеза (какое могло бы быть). 2. Феноменологические модели (если бы это произошло) 3. Информационные модели рассматривают объекты в виде «черного ящика» с входящим и выходящим 4. Упрощения (опустим для ясности некоторые детали) 5. Эвристическая модель (подтверждений нет, но модель позволяет понять суть) 6. Аналогия (учтём особенности предыдущего опыта) 7. Мысленный эксперимент (состоит в опровержении возможностей) 8. Демонстрация возможности (показать внутреннее непротиворечие) Типы шкал признаков: 1. Непрерывная шкала – признаки могут принимать любые вещественные значения. 2. Дискретные шкалы – признаки не являются вещественными: · Номинальные шкалы – применяются если число не является выражением какой-то меры а служит меткой варианта ответа на вопрос. · Порядковые – целое число отражает степень проявление определённого качества (степень уверенности). При представлении и обработке данных необходимо учитывать: 1) Не всегда признаковые таблицы полные (неопределённые данные) 2) Значение признаков измеряется с определенной точностью. 3) Данные допускают отклонения (данных) Представление данных Для представления данных часто используется признаковое геометрическое пространство.
В таком пространстве объекты представляются точкой, координаты которой являются значениями признаков. Если есть допустимость, то вместо точки изображаем геометрическую фигуру. Классом называют область в признаковом пространстве, объединённая схожестью свойствами объектов. Пример формального анализа
1. Метрика должна быть положительна 2. Симметрична 3. Метрика равна 0, если объекты совпадают 4. Для того чтобы величина была метрикой необходимо
13.09.2012 Тема: «Статистическая обработка данных» Параграф: Основные сведенья из теории вероятности. Случайное событие – событие, которое может произойти и может не произойти. Существует достоверное и невозможное событие. A, B, C – обозначение случайных событий. Случайные событие бывают совместные и несовместные (наступление одного исключает события другого). Противоположные событие в группе составляют достоверное событие (например: подбросить монету). Полная группа – это попарно несовместные события, которые вместе составляют достоверные события. Алгебра событий: Сумма событий -> C=A+B -> заключает в себе события и A и B. Произведение событий -> C=AB -> произойдет и событие A и событие B. Классическое определение вероятностей:
C=A+B -> C=A+B ->
Формула полной вероятности (формула Байеса):
Случайная величина – определяет: 1. Отношение строгого порядка, введенного на множестве элементарных событий. 2. Вероятностью того, что это случайная величина примет конкретное значение.
- для кубика.
- для монеты. Если случайная величина может принять любое значение из диапазона, тогда она называется аналоговой (или непрерывная).
Функция распределения -> Пример:
Для нахождения функции:
Числовые характеристики случайных величин делятся на три группы: 1. Центра группирования 2. Разбросы или вариации. 3. Статистические связи.
20.09.2012.
Числовые характеристики центра группирования: 1. Среднее арифметическое или математическое ожидание – если величина дискретная, то мы можем найти значение просуммировав все результаты и разделив на количество Для непрерывной случайной величины 2. Мода – применяются в случае, если закон распределения мультимодален и эти точки наибольшей вероятности. 3. Медиана – используя полученные данные в порядке возрастания. В качестве результата обработки используем результат расположенный посередине. ... Физический смысл – вероятность того, что величина будет меньше этого значения, равна вероятности появления большего значения. Квантиль уровня 0,9 – это значение в точке распределения 0,9 (Графически). 4. Для разрешения мультипликативного фактора мы логарифмируем значение закона распределения. (?)
5. Дисперсия – характеризует разброс значений распределения. 6. Среднеквадратическое отклонение -
Числовые характеристики … X – случайная величина рост. Y – случайная величина вес.
Ковариация - Нормирование - Коэффициент корреляции -
Закон больших чисел При достаточно большом количестве испытаний, математическое ожидание приближается к среднему значению вероятности.
X1, X2, …, Xn – закон распределения среднего арифметического не зависит от законов распределения каждого значения распределения.
(Центральная предельная теорема)
4.10.2012 11.10.12 01.01.12 Регрессионный анализ
…(график)…
Мы сделали статистическую оценку функции регрессии, полученную по выборке объему m.
08.11.12 … C1 – рост C2 – вес Набор образов относящихся к одному объекту, мы будем называть кластером. Два и более кластеров относящихся к одному объекту называется таксономом. … В общем случае, разделяющая поверхность задается в n-мерном пространстве и может быть достаточно сложной формой.
Предварительная обработка Целью предварительной обработки является понижения уровня шумов и повышение качества изображения. Рассматривают три типа шумов: 1. Мультипликативные – обусловленные неравномерной освещенностью объекта. 2. Аддитивные (Флюктуациационные) – внутренние шумы датчиков и вызванные внешними возмущениями. 3. Импульсные – обусловлены особенностями цифровой обработки сигнала. Если значения сигналов выходят за пределы или происходят сбои, то на сигнале изображения появляются яркие белые или черные точки (соль и перец).
15.11.12 /*Флюктуация – случайная часть сигнала (шум). Тренд – не случайная часть сигнала.*/ Предварительная обработка при аддитивной (флюктационной) помехе. Для того, чтобы интерпретировать результаты такой предварительной обработки, введем некоторые основные понятия из спектрального анализа.
…
Для того чтобы уменьшить уровень аддитивных (флюктуационных) помех, применяются методы линейной фильтрации. … Допустим у нас есть в дискретном виде 15 точек: 10 10 10 10 10 40 40 40 40 40 10 10 10 10 10 -3 0 2 1 -5 -1 -1 4 5 -2 4 -1 3 -5 5 7 10 12 11 5 39 39 44 45 38 14 9 7 5 15 Берем по три значения и производим усреднение (линейная фильтрация) (7+10+12)/3 = 10 (10+12+11)/3=11 (12+11+5)/3=9 … 10 11 9 18 26 41 43 42 … Проводя линейную фильтрацию, мы уменьшили флюктуацию, однако мы исказили сигнал. Три выбранные элемента (окно) называется апертурой обработки. Движение от начала, до конца строки называется сканированием. Процедура линейной фильтрации в общем случае описывается:
В спектральной области, отклик от линейного фильтра определяется:
… 1 – амплитудный спектр полезного сигнала. 2 – амплитудный спектр помехи. 3 – это модуль комплексного коэффициента передачи фильтра.
В результате такого фильтра, мы полностью убрали флюктуацию.
… На практике встречаются два вида шума: 1. Световой шум – локализован в области частот. 2. Белый шум – равномерно распределен, во все области пространственных частот. Полностью устранить шум невозможно, можно только уменьшит его мощность. Если шум световой и его спектр не пересекается со спектром полезного сигнала, то от него можно избавиться полностью методами линейной фильтрации. Если спектры полезного и шума пересекается, то уменьшение уровня шума введет к искажениям полезного сигнала. В практически важных задачах, параметрами фильтров выбирается с целью обработки, выбирается как компромисс между искажением полезного сигнала и улучшением шумов. Классификация фильтра В соответствии с видом комплексного коэффициента передачи, фильтры делятся на три основных типа. … - фильтр нижних частот (сначала 1, а потом 0) … - фильтр верхних частот (сначала 0, а потом 1) … - полосовой фильтр (селективный фильтр).
При обработке изображений используется операция двумерной свертки и двумерное преобразование Фурье.
… - пространственные частоты. … - изображение, которое мы обрабатываем. … - пространственные координаты.
Аналог импульсной характеристики фильтра называется функция рассеивания точки (задается в виде матрицы). Фильтры с четкими границами называются идеальными. Реальные имеют более размытые углы. 22.11.12 10 10 255 10 10 40 40 255 40 92 92 92 20 30 При таком виде помехи, линейная фильтрация бесполезна и даже вредна, так как она расширяет область локализации импульсной помехи, до величины апертуры обработки. Для предварительной обработки в этом случае применяется методы обработки, основанные на статистической оценке медианой распределения. Результат обработки в этом случае определяется местом элемента, в апертуре обработки. Методы основанные на ранге элемента (место в вариационном ряду) мы в дальнейшем будем называть ранговыми. Простейший вид ранговой обработки, это медианная фильтрация. 10 10 255 10 10 40 40 255 40 Пусть апертура обработки 3 Мы упорядочиваем элементы по возрастанию – строим вариационный ряд. Результат обработки является ранг. Недостатком медианной фильтрацией относится то, что она искажает острые углы объекта и может уничтожить мелкие его детали. В какой-то мере устраняет этот недостаток применение рациональной устраняет недостаток медианой фильтрации. В этом случае центральный момент обработки занимает сразу несколько мест в вариационном ряду. Конкретные параметры такого фильтра выбираются как компромисс между уровнем помех и искажениями полезного сигнала или изображения.
Предварительная обработка при мультипликативной помехе Источником мультипликативной помехи является освещенность. Как правило, изменение освещенности медленное и следовательно она лежит в области нижних частот. Объекты обработки, как правило, насыщенны деталями и следовательно находятся в области верхних частот. Методы линейной фильтрации в данном случае не применимы, так как они рассчитаны на аддитивную смесь сигнала и помехи. Поэтому применяется последующая последователь процедур: 1. Логарифмирования – ее целью является преобразования мультипликативной помехи в аддитивную. 2. Линейная фильтрация – ее целью является снижение низкочастотной помехи. 3. Экспондирование – возвращающая результат предыдущей обработки в исходное пространство. Этот метод часто применяется на практике и процедура получила название Гомоморфная фильтрация. В некоторых случаях операцию Экспондирования не применяют. В этом случае говорят, что дальнейшая обработка выполняется в пространстве плоскостей. …. Для того чтобы оценить качество предварительной обработки необходимо: 1. Иметь тестовые изображения. 2. Конкретизируется статистическая модель помех и в соответствии с этим в изображение вносится шум. 3. Производится предварительная обработка зашумленного изображения 4. Производится сравнения тестового изображения и изображения после предварительной обработки. Как правило для сравнения сигналов применяется среднеквадратическая ошибка.
Lx, Ly – количество ошибок в строке и столбце попиксельно. Целью предварительной обработки является снижение уровня помех. Снижение уровня помех оценивается по отношению сигнал-шум. …
P – средняя мощность сигнала. Для того, чтобы оценить отношение сигнал-шум нужно: 1. Оценить отношение на входе. 2. Оценить на выходе. 3.
29.11.12 Сегментация заключается в объединении данных в однородные по какому-либо признаку или набору признаков в области. Признаками сегментации могут быть: 1. Цвет 2. Признак контура (перепады интенсивности) – так где у нас перепад, мы ставим единицу, а где нету перепада ставим ноль. 3. Равноинтенсивности. 4. Признаки текстуры 5. Наличие или отсутствие объекта сегментации. Целью сегментации является сокращение объема обрабатываемых данных. … Результат контурной сегментации представляет собой матрицу того же размера, что и контурное изображение. В этой матрице в пикселях, в которых существует перепад 1, в остальных 0. Матрица называется контурным аппаратом. Для реализации этой процедуры могут применятся два подхода: 1. Дифференциальный 2. Корреляционно экстремальный Дифференциальный подход контурной сегментации. Этапы: 1. Дифференцирование. 2. Модуль. 3. Пороговое устройство. Использование дифференциального подхода обеспечивает высокую точность и высокое быстродействие, но делает низкую устойчивость. В рамках дифференциального подхода было разработано несколько методов позволяющих усилить перепад интенсивности с большей помехоустойчивостью, чем операции дифференцирования. В этом случае результат примерно такой: … К этим методам относятся операторы Собела, Кирхи, Робертса, курсовые операторы и т.д. Все эти методы отличаются только видом подчеркивания преобразования. Свойство дифференциальных операторов зависят от свойств обрабатываемого класса изображения и помех. Так как эти свойства от одного класса обрабатываемого изображения к другому меняются, не существуют одинаково пригодных для всех изображений. Поэтому на практике используют несколько операторов и выбирают тот оператор, который устраивает разработчика информационной системы больше. Однако в рамках этого подхода обеспечить высокую помехоустойчивость невозможно. Практический эксперимент: 10 10 10 10 10 40 40 40 40 40 10 10 10 10 10
0 0 15 45 15 0 0 -15 -45 -15 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 Если уровень помех высокий, то тогда применяют корреляционно экстремальный подход. Для начала мы составляем модель перепада интенсивности. Для сравнения двух функции используется среднеквадратическая ошибка.
М- количество точек в апертуре обработки. Модель перепада интенсивности сдвигается поэлементно в обрабатываемом изображении. В апертуре обработки вычисляется среднеквадратическая ошибка. Когда среднеквадратическая ошибка достигает минимума, мы установили перепад интенсивности в этой модели и проставляем 1 в соответствующую точку контурного аппарата. Помехоустойчивость этого метода зависит от апертуры обработки. Чем больше апертура обработки, тем меньше уровень шумов при сравнении с моделью.
Среднеквадратическая ошибка достигает минимума в том случае, если взаимно корреляционная функция достигает максимума. Для расчета корреляционной функции существуют быстрые алгоритмы на базе быстрого преобразования Фурье, это позволяет сократить вычислительные затраты. Метод соответственно называется корреляционно экстремальным.
06.12.12 Если уровень фона и величина перепада интенсивности не известны, то в рамках корреляционно экстремального метода необходимо произвести точечную оценку уровня фона и величины перепада в апертуре обработки. Цветовая сегментация Пиксель цветного изображения можно представить себе как точку в трехмерном цветовом пространстве. При выходе из однородной цветовой области меняются евклидовое расстояние между пикселями в трехмерном цветовом пространстве. Это расстояние можно трактовать как интенсивность. Поэтому результатом такого преобразования применимы рассмотренные ранее методы контурной сегментации. Поэтому результат такой обработки называют цветовыми контурами. Текстурная сегментация Текстуры подразделяют на три основных класса: 1. Упорядоченные или структурные текстуры. Эти текстуры состоят из ограниченного набора структурных элементов (структурных примитивов), которые находятся в отношении геометрического порядка. 2. Спектральные текстуры – может быть описана как квазипериодическая функция. Известно, что периодическую функцию можно представить в виде ряда Фурье, то-есть ограниченного числа гармонических колебаний. То-есть период следования и длительность сигнала может меняться в каких-то пределах. Поэтому спектральную текстуру как аналог ряда Фурье можно представить как линейную комбинацию квазигармонических колебаний. Квазигармонические колебания называются гармоникой, в которой амплитуда, частота и фаза могут меняться в определенных пределах по случайному закону. 3. Статистическая текстура – моделью такой текстуры является случайное поле, на границах которого происходит изменение числовой характеристики этого поля. Методы сегментации статистических структур Для того, чтобы произвести текстурную сегментацию выполняются следующие действия: 1. Выполняется апертура обработки. 2. В апертуре обработки производится статистическая оценка какого-либо признака вариации разброса. 3. Апертура обработки сдвигается вправо и действия повторяются до конца строки. Методы контурной сегментации. В рамках этого метода характеристики разброса преобразуются в интенсивность. Методы применяющие такое преобразование мы будем в дальнейшем называть детекторными. Действия: 1. Найти в апертуре среднее значение 2. Из текущих значений вычитаем текущее значение. На практике применяются следующие характеристики оценки разброса: 1. В апертуре обработки усредняются только положительные отклонения интенсивности от средне выборочного. Этот метод самый простой и быстрый, однако помехоустойчивость у него низкая. Эти действия называются амплитудное детектирование. 2. Усредняются модули отклонений интенсивностей от средне выборочного. Вычислительные затраты выше, но и помехоустойчивость повышается. Этот метод называется двух полупериодное. 3. Усредняет квадраты отклонений интенсивности от средне выборочного. Этот метод самый затратный и самый помехоустойчивый. При увеличении апертуры обработки возрастает объем вычислительных затрат, уменьшается дисперсия статистической оценки и увеличивается протяженность перепада. Повышение помехоустойчивости повышает качество выделения контура, а размытые перепады приводят к ухудшению этого качества. Поэтому размеры апертуры выбирают в процессе настройки как компромисс между этими факторами. Методы сегментации спектральных текстур. Реализуются следующие действия: 1. Формируется апертура обработки 2. В апертуре обработки формируется оценка остаточного сигнала. 3. Спектральный состав сигнала преобразуется в интенсивность. 4. Сдвинуть апертуру на один пиксель и вернутся к пункту 2 5. К результатам такой обработки применяются методы контурной сегментации. Разности в методе детектирования устройство преобразующее спектральный состав в интенсивность называется частотным детектором. Простейшим частотным детектором является колебательный контур. Рабочей областью является участок близкий к … Структурная текстура При сегментации структурных текстур применяются в основном эвристические алгоритмы. Из-за разнообразия текстур свести их к единым алгоритмам очень трудно. 6.09.2012 Тема: «Представление информации» Любое практическое исследование на начальном этапе включает стадию сбора информации. Для изучения предмета или объекта необходимо систематизировать данные. Для обобщения необходимо выделять совокупности общих или различных свойств объектов. Такие свойства называются признаками. Признаки бывают: 1. Детерминированные 2. Логические 3. Вероятностные 4. Структурные Одним из универсальных представлений является табличное. Чтобы извлечь информацию необходимо представить данные в виде модели. Модель – абстрактное представление данных с целью улучшения интерпретации. Виды моделей: · Математическая · Физическая · Информационная Классификация моделей: 1. Гипотеза (какое могло бы быть). 2. Феноменологические модели (если бы это произошло) 3. Информационные модели рассматривают объекты в виде «черного ящика» с входящим и выходящим 4. Упрощения (опустим для ясности некоторые детали) 5. Эвристическая модель (подтверждений нет, но модель позволяет понять суть) 6. Аналогия (учтём особенности предыдущего опыта) 7. Мысленный эксперимент (состоит в опровержении возможностей) 8. Демонстрация возможности (показать внутреннее непротиворечие) Типы шкал признаков: 1. Непрерывная шкала – признаки могут принимать любые вещественные значения. 2. Дискретные шкалы – признаки не являются вещественными: · Номинальные шкалы – применяются если число не является выражением какой-то меры а служит меткой варианта ответа на вопрос. · Порядковые – целое число отражает степень проявление определённого качества (степень уверенности). При представлении и обработке данных необходимо учитывать: 1) Не всегда признаковые таблицы полные (неопределённые данные) 2) Значение признаков измеряется с определенной точностью. 3) Данные допускают отклонения (данных) Представление данных Для представления данных часто используется признаковое геометрическое пространство.
В таком пространстве объекты представляются точкой, координаты которой являются значениями признаков. Если есть допустимость, то вместо точки изображаем геометрическую фигуру. Классом называют область в признаковом пространстве, объединённая схожестью свойствами объектов. Пример формального анализа
1. Метрика должна быть положительна 2. Симметрична 3. Метрика равна 0, если объекты совпадают 4. Для того чтобы величина была метрикой необходимо
13.09.2012 Тема: «Статистическая обработка данных» Параграф: Основные сведенья из теории вероятности. Случайное событие – событие, которое может произойти и может не произойти. Существует достоверное и невозможное событие. A, B, C – обозначение случайных событий. Случайные событие бывают совместные и несовместные (наступление одного исключает события другого). Противоположные событие в группе составляют достоверное событие (например: подбросить монету). Полная группа – это попарно несовместные события, которые вместе составляют достоверные события. Алгебра событий: Сумма событий -> C=A+B -> заключает в себе события и A и B. Произведение событий -> C=AB -> произойдет и событие A и событие B. Классическое определение вероятностей:
C=A+B -> C=A+B ->
Формула полной вероятности (формула Байеса):
Случайная величина – определяет: 1. Отношение строгого порядка, введенного на множестве элементарных событий. 2. Вероятностью того, что это случайная величина примет конкретное значение.
- для кубика.
- для монеты. Если случайная величина может принять любое значение из диапазона, тогда она называется аналоговой (или непрерывная).
Функция распределения -> Пример:
Для нахождения функции:
Числовые харак
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.46.174 (0.026 с.) |

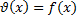
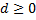

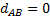 (A=B)
(A=B)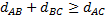
 -> n- общее количество, m – благоприятствующие события.
-> n- общее количество, m – благоприятствующие события.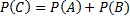 – если они не совместны.
– если они не совместны. – если они не зависимы
– если они не зависимы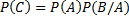 – при условии, что событие А уже произошло.
– при условии, что событие А уже произошло.
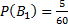

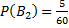
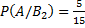

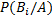 – вероятность того, что студент сдавший экзамен будет с группы с плохой посещаемостью.
– вероятность того, что студент сдавший экзамен будет с группы с плохой посещаемостью.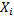
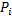


 – это функция, полученная как попадание случайной величины в бесконечно малый интервал.
– это функция, полученная как попадание случайной величины в бесконечно малый интервал.
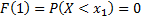 – не бывает грани меньше единице.
– не бывает грани меньше единице.


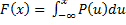
 – базовая формула нахождения математического ожидания.
– базовая формула нахождения математического ожидания.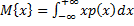
 .
.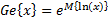

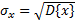 .
. – значение отклонения
– значение отклонения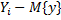 – значение отклонения
– значение отклонения

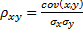 .
.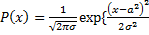
 выборка, состоящая из n единиц, которая имеет два значения X и Y. Полученное значение роста мы упорядочиваем в порядке возрастания
выборка, состоящая из n единиц, которая имеет два значения X и Y. Полученное значение роста мы упорядочиваем в порядке возрастания  . Начинаем обрабатывать данные для значения роста
. Начинаем обрабатывать данные для значения роста  (студенты минимального роста). Получаем значение весов студентов с ростом
(студенты минимального роста). Получаем значение весов студентов с ростом 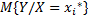 - условное математическое ожидания случайной величины Y (вес), при котором случайное значение X (рост) имеет значение
- условное математическое ожидания случайной величины Y (вес), при котором случайное значение X (рост) имеет значение  .
. – полученную функцию назовем функцией регрессии случайной величины Y на случайную величину X.
– полученную функцию назовем функцией регрессии случайной величины Y на случайную величину X. - условное математическое ожидания случайной величины X (рост), при котором случайное значение Y (вес) имеет значение
- условное математическое ожидания случайной величины X (рост), при котором случайное значение Y (вес) имеет значение  .
.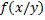 – функции регрессии веса на рост.
– функции регрессии веса на рост.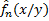 – статистическая оценка функции регрессии на рост по выборке объема n.
– статистическая оценка функции регрессии на рост по выборке объема n.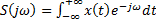 - преобразование Фурье.
- преобразование Фурье.
 – обрабатываемый сигнал
– обрабатываемый сигнал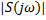 – амплитудный спектр
– амплитудный спектр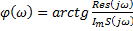
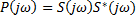 – спектр мощности
– спектр мощности - реализовано физически и устройство называется конвольвером.
- реализовано физически и устройство называется конвольвером. – называется импульсной характеристикой фильтра.
– называется импульсной характеристикой фильтра.
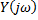 - спектральная плотность выходного сигнала
- спектральная плотность выходного сигнала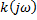 - комплексным коэффициентом передачи. Преобразование от Фурье, импульсной характеристики фильтра
- комплексным коэффициентом передачи. Преобразование от Фурье, импульсной характеристики фильтра - спектральная плотность входного сигнала
- спектральная плотность входного сигнала  .
.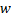 – точка среза.
– точка среза.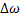 – ширина пропускания.
– ширина пропускания. 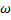 – резонансная частота.
– резонансная частота.
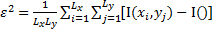 ???
??? (по амплитутде)
(по амплитутде)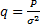 (по мощности)
(по мощности)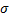 –дисперсия во втором случае.
–дисперсия во втором случае.


 -1 1
-1 1  – маска. Результат будет выставляться в 1.
– маска. Результат будет выставляться в 1.

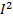 - средняя мощность строки изображения в апертуре обработки.
- средняя мощность строки изображения в апертуре обработки.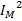 – среднее значение модели
– среднее значение модели – средне корреляционная функция …
– средне корреляционная функция …



