
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод моментов для точечной оценки параметров распределенияСодержание книги
Поиск на нашем сайте
Можно доказать, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов того же порядка. На этом основан метод моментов, предложенный К. Пирсоном. Достоинство метода - сравнительная его простота. Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка. А. Оценка одного параметра. Пусть задан вид плотности распределения f (x,θ), определяемой одним неизвестным параметром θ. Требуется найти точечную оценку параметра θ. Для оценки одного параметра достаточно иметь одно уравнение относительно этого параметра. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: ν 1 = М 1. Учитывая, что ν 1 = М (X) (см. гл. VIII, § 10), М 1 = М (X)= Математическое ожидание М (X), как видно из соотношения
есть функция от θ, поэтому (*) можно рассматривать как уравнение с одним неизвестным θ. Решив это уравнение относительно параметра θ, тем самым найдем его точечную оценку θ *, которая является функцией от выборочной средней, следовательно, и от вариант выборки: θ *= Пример 1. Найти методом моментов по выборке х 1, х 2,..., хп точечную оценку неизвестного параметра λ, показательного распределения, плотность распределения которого Решение. Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: ν 1 = М 1. Учитывая,, М 1 = М (X)= Приняв во внимание, что математическое ожидание показательного распределения равно 1/λ (см. гл. XIII, § 3), имеем 1/λ= Отсюда λ=1/ Итак, искомая точечная оценка параметра λпоказательного распределения равна величине, обратной выборочной средней: λ*=1/ Б. Оценка двух параметров. Пусть задан вид плотности распределения f (х; θ 1, θ 2), определяемой неизвестными параметрами θ 1 и θ 2. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:
ν 1 = М 1, μ 2 =m 2. Учитывая, что что ν 1 = М (X), μ 2 = D (Х)(см. гл. VIII, § 10), М 1 =
Математическое ожидание и дисперсия есть функции от θ 1 и θ 2, поэтому (**) можно рассматривать как систему двух уравнений с двумя неизвестными θ 1 и θ 2. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки θ 1* и θ 2*. Эти оценки являются функциями от вариант выборки: θ 1*= ψ 1(х 1, х 2,..., хп) θ 1* = ψ 2(х 1, х 2,..., хп) Пример 2. Найти методом моментов по выборке х 1, х 2,..., хп точечные оценки неизвестных параметров а и σ нормального распределения
Решение. Приравняем начальные теоретические и эмпирические моменты первого порядка, а также центральные и эмпирические моменты второго порядка: ν 1 = М 1, μ 2 =m 2. Учитывая, что ν 1 = М (X), μ 2 = D (Х), М 1 =
Приняв во внимание, что математическое ожидание нормального распределения равно параметру а, дисперсия равна σ 2 (см. гл. XII, § 2),имеем: а = Итак, искомые точечные оценки параметров нормального распределения: а* = Замечание 1. Для оценок, неизвестных параметров можно приравнивать не только сами моменты, но и функции от моментов. В частности, этим путем получают состоятельные оценки характеристик распределений, которые являются функциями теоретических моментов. Например, асимметрия теоретического распределения (см. гл. XII, § 9)
есть функция от центральных моментов второго и третьего порядков. Заменив эти теоретические моменты соответствующими эмпирическими моментами, получим точечную оценку асимметрии
Замечание 2. Учитывая, что
Далее эта оценка будет принята в качестве определения асимметрии эмпирического распределения (см. гл. XVII, § 9).
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 3165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.63.162 (0.009 с.) |

 (см. гл. XVII, § 2), получим
(см. гл. XVII, § 2), получим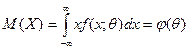 ,
,
 (x ≥0).
(x ≥0). (**)
(**)

 .
.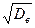

 .
. , последнюю формулу можно записать в виде
, последнюю формулу можно записать в виде



