
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность оценки, доверительная вероятность (надежность). Доверительный интервалСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше,- точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Интервальной называют оценку, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок (смысл этих понятий выясняется ниже). Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом (Θ может быть и случайной величиной). Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ - Θ*|. Другими словами, если δ >0 и |Θ - Θ*|< δ, то чем меньше δ, тем оценка точнее. Таким образом, положительное число δ характеризует точность оценки. Однако статистические методы не позволяют категорически утверждать, что оценка Θ * удовлетворяет неравенству |Θ - Θ*|< δ; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется. Надежностью (доверительной вероятностью)оценки Θ по Θ* называют вероятностьγ,с которой осуществляется неравенство |Θ - Θ*|< δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999. Пусть вероятность того, что |Θ - Θ*|< δ, равна γ: Р [|Θ - Θ*|< δ ]= γ. Заменив неравенство |Θ - Θ*|< δ равносильным ему двойным неравенством -δ <Θ - Θ*< δ, или Θ*- δ <Θ< Θ* + δ, имеем Р [Θ* - δ <Θ< Θ* + δ ] = γ. Это соотношение следует понимать так: вероятность того, что интервал(Θ*- δ, Θ*+ δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ. Доверительным называют интервал (Θ*- δ, Θ*+ δ), который покрывает неизвестный параметр с заданной надежностью γ. Замечание. Интервал (Θ*- δ, Θ*+ δ) имеет случайные концы (их называют доверительными границами). Действительно, в разных выборках получаются различные значения Θ*. Следовательно, от выборки к выборке будут изменяться и концы доверительного интервала, т. е. доверительные границы сами являются случайными величинами - функциями от х 1, x 2,..., хn. Так как случайной величиной является не оцениваемый параметр Θ, а доверительный интервал, то более правильно говорить не о вероятности попадания Θ в доверительный интервал, а о вероятности того, что доверительный интервал покроет Θ. Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.
§ 15. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ этого распределения известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней Будем рассматривать выборочную среднюю Примем без доказательства, что если случайная величина X распределена нормально, то выборочная средняя M ( Потребуем, чтобы выполнялось соотношение Р (|Х - а| < δ) = γ, где γ - заданная надежность. Пользуясь формулой (см. гл. XII, § 6) Р (|Х-а| < δ) = 2 Ф (δ/σ), заменив X на Р (|Х-а|) <δ) = 2 Ф (δ где t = δ Найдя из последнего равенства Р (| Приняв во внимание, что вероятность P задана и равна γ, окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через
Смысл полученного соотношения таков: с надежностью γ можно утверждать, что доверительный интервал ( Итак, поставленная выше задача полностью решена. Укажем еще, что число t определяется из равенства 2 Ф (t) = γ. или Ф (t) = γ / 2; по таблице функции Лапласа (см. приложение 2) находят аргумент t, которому соответствует значение функции Лапласа, равное γ / 2. Замечание 1. Оценку 1) при возрастании объема выборки п число δ убывает и, следовательно, точность оценки увеличивается; 2) увеличение надежности оценки γ = 2 Ф (t) приводит к увеличению t (Ф (t) — возрастающая функция), следовательно, и к возрастанию δ; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности. Пример. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением σ = 3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним Решение. Найдем t. Из соотношения 2Ф(t)=0,95 получим Ф(t) = 0,475. По таблице приложения 2 находим t =1,96. Найдем точность оценки:
Доверительный интервал таков: (
Таким образом, значения неизвестного параметра а, согласующиеся с данными выборки, удовлетворяют неравенству 3,12 < а < 5,08. Подчеркнем, что было бы ошибочным написать Р (3, 12< а < 5,08) = 0,95. Действительно, так как а - постоянная величина, то либо она заключена в найденном интервале (тогда событие 3,12 < а < 5,08 достоверно и его вероятность равна единице), либо в нем не заключена (вэтом случае событие 3,12 < а < 5,08 невозможно и его вероятность равна нулю). Другими словами, доверительную вероятность не следует связывать с оцениваемым параметром; она связана лишь с границами доверительного интервала, которые, как уже было указано, изменяются от выборки к выборке. Поясним смысл, который имеет заданная надежность. Надежность γ = 0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала. Замечание 2. Если требуется оценить математическое ожидание с наперед заданной точностью δ и надежностью γ, то минимальный объем выборки, который обеспечит эту точность, находят по формуле
(следствие равенства
§ 16. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение а неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в которомσ предполагалось известным. Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t):
которая имеет распределение Стьюдента с k = n- 1 степенями свободы (см. пояснение в конце параграфа); здесь Плотность распределения Стьюдента
где Мы видим, что распределение Стьюдента определяется параметром n - объемом выборки (или, что то же, числом степеней свободы k = n- 1) и не зависит от неизвестных параметров а и σ; эта особенность является его большим достоинством. Поскольку S (t,n) - четная функция от t, вероятность осуществления неравенства
Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим
Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал Здесь случайные величины Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n =16 найдены выборочная средняя Решение. Найдем tγ. Пользуясь таблицей приложения 3, по γ = 0,95 и n = 16 находим tγ =2,13. Найдем доверительные границы:
Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале 19,774 < а < 20,626. Замечание. Из предельных соотношений
следует, что при неограниченном возрастании объема выборки n распределение Стьюдента стремится к нормальному. Поэтому практически при n > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением. Однако важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений n, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т.е. к повышению точности оценки. Например, если n = 5 и γ = 0,99, то, пользуясь распределением Стьюдента, найдем t γ = 4,6, а используя функцию Лапласа, найдем tγ = 2,58, т.е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента. То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке. Пояснение. Ранее было указано (см. гл. XII, § 14), что если Z - нормальная величина, причем M (Z) = 0, σ (Z)=1, а V - независимая от Z величина, распределенная по закону χ2 с k степенями свободы, то величина
распределена по закону Стьюдента с k степенями свободы. Пусть количественный признак X генеральной совокупности распределен нормально, причем М (Х) =а, σ (Х) = σ. Если из этой совокупности извлекать выборки объема n и по ним находить выборочные средние, то можно доказать, что выборочная средняя распределена нормально, причем (см. гл. VIII, § 9)
Тогда случайная величина
также имеет нормальное распределение как линейная функция нормального аргумента
независимы (S 2 - исправленная выборочная дисперсия) и что величина V распределена по закону χ2 с k = n- 1 степенями свободы. Следовательно, подставив (**) и (***) в (*), получим величину
которая распределена по закону Стьюдента с k = n- 1 степенями свободы.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 4125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.011 с.) |

 . Поставим своей задачей найти доверительные интервалы, покрывающие параметр а с надежностью γ.
. Поставим своей задачей найти доверительные интервалы, покрывающие параметр а с надежностью γ. (
(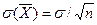 .
. ) = 2 Ф (t),
) = 2 Ф (t), , можем написать
, можем написать ) = 2 Ф (t).
) = 2 Ф (t).
 ,
,  ) покрывает неизвестный параметр а; точность оценки
) покрывает неизвестный параметр а; точность оценки  называют классической. Из формулы
называют классической. Из формулы  .
.
 ).
). ,
,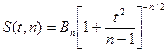 ,
, .
. определяется так (см. гл. § XI, 2, замечание):
определяется так (см. гл. § XI, 2, замечание): .
. .
. , покрывающий неизвестный параметр а снадежностью γ.
, покрывающий неизвестный параметр а снадежностью γ. .
.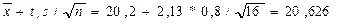 .
.
 .
. (*)
(*) ,
,  .
. (**)
(**)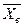 (см. гл. XII, § 10, замечание), причем М (Z) = 0, σ(Z)=l. Доказано, что случайные величины Z и
(см. гл. XII, § 10, замечание), причем М (Z) = 0, σ(Z)=l. Доказано, что случайные величины Z и (***)
(***) ,
,


