
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теорема сложения вероятностей несовместных событий Суммой A + B двух событий A и B называют событие, состоящее в появления события A, или события B, или обоих этих событий. Например, если из орудия произведены два выстрела и A – попадание при первом выстреле, B – попадание при втором выстреле, то A + B – попадание при первом выстреле, или при втором, ил в обоих выстрелах. В частности, если два события A и B – несовместные, то A + B – событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного их этих событий. Например, событие A + B + C состоит в появлении одного из следующих событий: A, B, C, A и B, A и C, B и C, A и B и C. Пусть события A и B – несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие B? Ответ на этот вопрос дает теорема сложения. Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: P (A + B) = P (A) + P (B). Доказательство. Введем обозначения: n – общее число возможных элементарных исходов испытания; m 1 – число исходов, благоприятствующих событию A; m 2 – число исходов, благоприятствующих событию B. Число элементарных исходов, благоприятствующих наступлению либо события A, либо события B, равно m 1 + m 2. Следовательно, P (A + B) = (m 1 + m 2)/ n = m 1/ n + m 2/ n. Приняв во внимание, что m 1/ n = P (A) и m 2/ n = P (B), окончательно получим P (A + B) = P (A) + P (B). Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий: P (A 1 + A 2 + … + An) = P (A 1) + P (A 2) + … + P (An). Доказательство. Рассмотрим три события: A, B и C. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, A, B и C,равносильно наступлению одного из двух событий, A + B и C,поэтому в силу указанной теоремы P (A + B + C) = P [(A + B) + C ] = P (A + B) + P (C) = P (A) + P (B) + P (C). Для произвольного числа попарно несовместных событий доказательство проводится методом математической индукции. Пример 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Решение. Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие A) P (A) = 10/30 = 1/3. Вероятность появления синего шара (событие B) P (B) = 5/30 = 1/6. События A и B несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 1/3 + 1/6 = ½. Пример 2. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35.Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область. Решение. Событие A – «стрелок попал в первую область» и B – «стрелок попал во вторую область» - несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 0,45 + 0,35 = 0,80.
Полная группа событий
Теорема. Сумма вероятностей событий A 1, A 2, …, An, образующих полную группу, равна единице: P (A 1) + P (A 2) + … + P (An) = 1. Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то P (A 1) + P (A 2) + … + P (An) = 1. (*) Любые два события полной группы несовместны, поэтому можно применить теорему сложения: P (A 1 + A 2 + … + An) = P (A 1) + P (A 2) + … + P (An). (**) Сравнивая (*) и (**), получим P (A 1) + P (A 2) + … + P (An) = 1. Пример. Консультационный пункт института получает пакеты с контрольными работами из городов A, B и C. Вероятность получения пакета из города A равна 0,7, из города B – 0,2. Найти вероятность того, что очередной пакет будет получен из города C. Решение. Событие «пакет получен из города A», «пакет получен из города B», «пакет получен из города C» образуют полную группу, поэтому сумма вероятностей этих событий равна единице: 0,7 + 0,2 + p = 1. Отсюда искомая вероятность p = 1 – 0,9 = 0,1.
Противоположные события Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать Пример 1. Попадание и промах при выстреле по цели – противоположные события. Если A – попадание, то Пример 2. Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» - противоположные. Теорема. Сумма вероятностей противоположных событий равна единице: P (A) + P ( Доказательство. Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице (см. § 2). Замечание 1. Если вероятность одного из двух противоположных событий обозначена через p, то вероятность другого события обозначают через q. Таким образом, в силу предыдущей теоремы p + q =1. Пример 3. Вероятность того, что день будет дождливым, p = 0,7.Найти вероятность того, что день будет ясным. Решение. События «день дождливый» и «день ясный» - противоположные, поэтому искомая вероятность q = 1 – p = 1 – 0,7 = 0,3. Замечание 2. При решении задач на отыскание вероятности события A часто выгодно сначала вычислить вероятность P (A) = 1 – P ( Пример 4. В ящике имеется n деталей, из которых m стандартных. Найти вероятность того, что среди k наудачу извлеченных деталей есть хотя бы одна стандартная. Решение. Событие «среди извлеченных деталей есть хотя бы одна стандартная» и «среди извлеченных деталей нет ни одной стандартной» - противоположные, обозначим первое событие через A, а второе – через Очевидно, P (A) = 1 – P ( Найдем P ( Искомая вероятность P (A) = 1 - P (
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 763; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

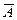 .
. Число нестандартных деталей равно n – m; из этого числа деталей можно
Число нестандартных деталей равно n – m; из этого числа деталей можно  способами извлечь k нестандартных деталей. Поэтому вероятность того, что среди извлеченных k деталей нет ни одной стандартной, равна P (
способами извлечь k нестандартных деталей. Поэтому вероятность того, что среди извлеченных k деталей нет ни одной стандартной, равна P (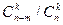 .
.


