Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы сложения и умножения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Суммой двух событий А и В называется событие С, состоящее в наступлении события А, или события В, или обоих событий вместе. Обозначается А + В = С. Например, если событие А – попадание в цель при первом выстреле, событие В – попадание в цель при втором выстреле, то событие С = А + В есть попадание в цель либо при первом выстреле, либо при втором, либо при обоих выстрелах. Если события Определение. Суммой нескольких событий Определение. Произведением двух событий А и В называется событие С, состоящее в совместном наступлении события А и события В. Обозначается Например, в саду высадили два дерева. Событие А - первое дерево в этом году даст плоды, событие В - второе дерево в этомгоду даст плоды. Событие Определение. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий. Обозначается С = Теорема сложения вероятностей несовместных событий. Вероятность суммы
Следствие 1. Если события
Следствие 2. Сумма вероятностей противоположных событий равна единице:
Теорема сложения вероятностей совместных событий. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления:
Определение. Два события называются независимыми, если вероятность наступления одного из них (причем любого) не зависит от того, произошло или не произошло другое событие. В противном случае события называются зависимыми. Например, фары трактора или автомобиля подсоединены параллельно. Отказ в работе левой фары – событие А, отказ в работе правой фары – событие В. События А и В независимые. Определение. Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация из остальных событий (содержащая либо все события, либо часть из них) есть события независимые. Например, на каждом из трех стеллажей склада находится по 25 поршней первого и второго допуска. Из каждого стеллажа берут по одному поршню. Рассмотрим 3 события: А – взятый с первогостеллажа поршень имеет первый допуск, В – взятый со второго стеллажа поршень имеет второй допуск, С – взятый с третьего стеллажа поршень имеет первый допуск. События А, В, С – независимые в совокупности. Определение. Условной вероятностью Теорема умножения вероятностей независимых событий. Вероятность произведения (совместного наступления) двух независимых событий равна произведению вероятностей этих событий:
Следствие. Вероятность произведения (совместного наступления) нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Теорема. Вероятность появления хотя бы одного из событий
Теорема умножения вероятностей зависимых событий. Вероятность произведения (совместного наступления) двух зависимых событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Пример 14.7. В урне 40 шаров: 15 красных, 5 зеленых и 20 белых. Какова вероятность того, что из урны будет извлечен цветной шар? Решение. Извлечение цветного шара означает появление либо красного, либо зеленого. Вероятность извлечения красного шара (событие А):
Пример 14.8. Вероятности появления каждого из трех независимых событий а) только одного из этих событий; б) двух событий; в) хотя бы одного события. Решение.а) Из условия задачи
Пусть событие В – появление только одного из этих трех событий, а так как появится может или
Отсюда в силу несовместности и независимости событий
б) Пусть событие
Отсюда в) Пусть событие Поэтому
Пример 14.9. Среди 15 микрокалькуляторов, имеющихся в вычислительной лаборатории, лишь 6 новых, а остальные – бывшие в употреблении. Наугад взято три микрокалькулятора. Какова вероятность, что все они окажутся новыми? Решение. Рассмотрим события:
Тогда вероятность достать новый микрокалькулятор при первой попытке равна
Вероятность того, что второй микрокалькулятор будет новым, при условии, что первым уже был отобран новый микрокалькулятор равна (условная вероятность события
Вероятность того, что третьим будет отобран новый микрокалькулятор, при условии, что уже отобраны два новых микрокалькулятора, т.е. условная вероятность события
Искомая вероятность, что все три отобранных микрокалькулятора окажутся новыми, равна
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.01 с.) |

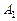 и
и  – несовместные, то событие
– несовместные, то событие  называется событие С, состоящее в наступлении хотя бы одного из этих событий. Обозначается С =
называется событие С, состоящее в наступлении хотя бы одного из этих событий. Обозначается С =  .
.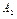 …
… 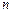 несовместных событий равна сумме вероятностей этих событий.
несовместных событий равна сумме вероятностей этих событий.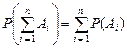 .
. .
.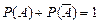 .
. .
. или
или  называется вероятность события А, вычисленной в предположении, что событие В уже наступило.
называется вероятность события А, вычисленной в предположении, что событие В уже наступило.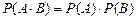 .
. .
. произведением вероятностей противоположных событий
произведением вероятностей противоположных событий  ,
, 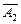 , …
, … 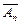 , т.е.
, т.е. .
.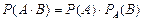 или
или  .
. . Вероятность извлечения зеленого шара (событие В):
. Вероятность извлечения зеленого шара (событие В): 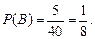 Так как события несовместны, то получаем
Так как события несовместны, то получаем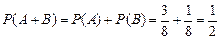 .
.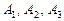 соответственно равны 0,7; 0,8; 0,9. Найти вероятность появления
соответственно равны 0,7; 0,8; 0,9. Найти вероятность появления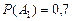 ,
,  ,
, 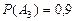 ,
, ,
, 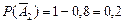 ,
, 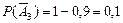 .
.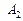 , или
, или 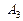 , то
, то .
.
 – появление только двух событий. Тогда
– появление только двух событий. Тогда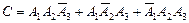 .
.
 – появления хотя бы одного события. Тогда противоположное событие
– появления хотя бы одного события. Тогда противоположное событие  – ни одно событие не появилось в испытаниях, т.е.
– ни одно событие не появилось в испытаниях, т.е.  .
. . Отсюда
. Отсюда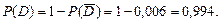
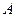 – первый из взятых микрокалькуляторов новый;
– первый из взятых микрокалькуляторов новый;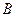 – второй микрокалькулятор новый;
– второй микрокалькулятор новый; – третий микрокалькулятор новый.
– третий микрокалькулятор новый. .
.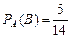 .
.