
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи по теории вероятностей и математической статистике .Содержание книги
Поиск на нашем сайте
1. Отдел технического контроля получил партию из 1000 деталей. Вероятность того, что взятая наугад деталь окажется дефектной, равна 0,001. Найти вероятность того, что в партии дефектны: а) хотя бы одна деталь; б) две детали; в) более двух деталей. 2. На экзамене предлагаются задачи по трем темам: по первой теме – 15 задач; по второй теме – 20 задач; по третьей теме – 25 задач. Вероятность того, что студент сможет решить задачу по первой теме равна 0,7; по второй – 0,9; по третьей – 0,3. Студент справился с задачей. Какова вероятность того, что ему попалась задача по первой теме? 3. В каждой из двух урн содержится восемь черных и два белых шара. Из второй урны наудачу переложили в первую один шар, а затем из первой урны вынули наугад один шар. Найти вероятность того, что вынутый из первой урны шар окажется черным. 4. Электронное устройство состоит из четырех элементов работающих независимо. Вероятность безотказной работы в течение месяца соответственно равны 0,6 для первого элемента; 0,8 для второго; 0,7 для третьего и 0,9 для четвертого. Найти вероятность того, что в течение месяца будут безотказно работать: а) все четыре элемента; б) только один элемент; в) не менее двух элементов. 5. Вероятность поражения мишени при одном выстреле равна 0,9. Найти вероятность того, что при ста выстрелах мишень будет поражена 90 раз. 6. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле только из первого орудия равна 0,7; из второго – 0,6; из третьего – 0,8. Найти вероятность того, что: 1) хотя бы один снаряд попадет в цель; 2) только два снаряда попадут в цель; 3) все три снаряда попадут в цель. 7. Монету бросают шесть раз. Найти вероятность того, что «герб» выпадет: а) три раза; б) менее трех раз; в) не менее трех раз. 8. Прибор состоит из двух узлов. Если отказывает хотя бы один узел прибор не функционирует. Вероятность безотказной работы в течение дня равны соответственно для первого узла 0,9, а для второго 0,8. В течение дня прибор отказал. Найти вероятность того, что отказал первый узел, а второй исправен. Отказы узлов происходят независимо. 9. На вычислительный центр поставлены дисплеи двух производителей: 30% - от первого, а остальные – от второго поставщика. Вероятность наличия скрытого дефекта дисплея от первого поставщика равна 0,05, а от второго 0,01. Какова вероятность того, что случайно выбранный дисплей имеет скрытый дефект? 10. Какова вероятность того, что при 100 бросаниях монеты «цифра» выпадет: а) хотя бы один раз; б) не менее 45 и не более 55 раз? 11-20. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x); 2) схематично построить графики функций f(x) и F(х);
11.
12.
13.
14.
15.
16.
17.
18.
19.
20. 21-30. Заданы математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. 1) Написать плотность распределения вероятностей и схематично построить ее график. 2) Найти вероятность того, что Х примет значение из интервала 3) Найти вероятность того, что Х примет значение, превышающее β; 4) Найти интервал, симметричный относительно математического ожидания а, в котором с вероятностью 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31-40. Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41-50. В результате проверки n контейнеров установлено, что число изделий Х, поврежденных при транспортировке и разгрузке, имеет эмпирическое распределение, сведенное в таблицу, где
41. n=50; α=0,05
42. n=200; α=0,02
43. n=100; α=0,05
44. n=200; α=0,01
45. n=100; α=0,02
46. n=100; α=0,05
47. n=150; α=0,02
48. n=50; α=0,05
49. n=200; α=0,01
50. n=100; α=0,02
51-60. Данные наблюдений над двумерной случайной величиной
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
Темы практических занятий.
6. Содержание и оформление контрольных работ 6.1. Требования к оформлению контрольных работ: контрольные работы выполняются в тетради (12 л.) на обложке необходимо указать № к.р., свой факультет, специальность, шифр зачетной книжки, № варианта, ФИО.
6.2. Требования к структуре контрольной работы: При выполнении работы необходимо приводить основные теоретические моменты, промежуточные математические доказательства, методики, формулы, расчеты. В конце работы указывается список использованных источников, ставится число и личная подпись.
7.Вопросы для подготовки к экзамену (зачету). 1. Классическое определение вероятности. 2. Геометрическая вероятность. Задача о встрече. 3. Теоремы сложения вероятностей. 4. Теоремы умножения вероятностей. 5. Формула полной вероятности. 6. Формула Бейеса. 7. Повторение испытаний. Формула Бернулли. 8. Общая теорема о повторении опытов. Производящая функция. 9. Локальная теорема Лапласа. 10. Интегральная теорема Лапласа. 11. Закон распределения вероятностей дискретной случайной величины. 12. Поток событий. 13. Числовые характеристики дискретных случайных величин(математическое ожидание, дисперсия). 14. Мода и медиана. 15. Начальные и центральные моменты. 16. Неравенство Чебышева. 17. Теорема Чебышева. 18. Следствия закона больших чисел: теоремы Бернулли и Пуассона. 19. Характеристические функции. 20. Центральная предельная теорема. 21. Функция распределения вероятностей случайной величины. 22. Плотность распределения случайной величины. 23. Числовые характеристики непрерывных случайных величин. 24. Свойства числовых характеристик (математическое ожидание, дисперсия). 25. Нормальное распределение. 26. Правило «трех сигма». 27. Равномерное распределение. 28. Закон Пуассона. 29. Функция одного случайного аргумента. 30. Функция двух случайных аргументов. 31. Закон распределения двумерной случайной величины. 32. Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма. 33. Числовые характеристики статистического распределения. 34. Критерии согласия(критерий Пирсона). 35. Критерии согласия(критерий Колмогорова). 36. Функция распределения системы двух случайных величин. 37. Плотность распределения системы двух случайных величин. 38. Зависимые и независимые случайные величины. 39. Корреляционный момент. Коэффициент корреляции. 40. Обработка опытов. Оценки для математического ожидания и дисперсии. 41. Доверительный интервал. Доверительная вероятность. 42. Характеристики случайных функций. 43. Линейные и нелинейные операторы. 44. Линейные преобразования случайных функций. 45. Характеристики производной от случайной функции. 46. Характеристики интеграла от случайной функции. 47. Сложений случайных функций. 8. Рекомендуемая литература Учебники
Задачники
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2001.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.34 (0.008 с.) |

 ).
).




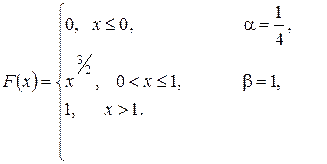




 .
. будут заключены значения случайной величины Х.
будут заключены значения случайной величины Х.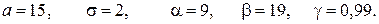






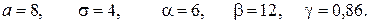


 и объем выборки n. Найти доверительный интервал для оценки неизвестного математического ожидания а с доверительной вероятностью
и объем выборки n. Найти доверительный интервал для оценки неизвестного математического ожидания а с доверительной вероятностью 






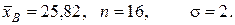


 - количество поврежденных изделий в одном контейнере,
- количество поврежденных изделий в одном контейнере,  - частота этого события, т.е. число контейнеров, содержащих
- частота этого события, т.е. число контейнеров, содержащих  .
.


