
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы полной вероятности и Байеса.Содержание книги Поиск на нашем сайте
В торговую фирму поступили телевизоры от трех поставщиков:10% от первого, 40% от второго и 50% от третьего. Практика показала, что телевизоры, поступающие от первого, второго и третьего поставщиков, не потребуют ремонта в течении гарантийного срока, соответственно в 70%,90% и 80% случаев. 1) найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока; 2) проданный телевизор не потребовал ремонта в течение гарантийного срока, от какого поставщика вероятнее всего поступил телевизор?. Решение. 1) обозначим через А- «телевизор не потребует ремонта в течение гарантийного срока». Возможны следующие предположение (гипотезы) о поставщике поступившего в торговую фирму телевизора. H1= «телевизор поступил от первого поставщика»; H2= «телевизор поступил от второго поставщика»; H3= «телевизор поступил от третьего поставщика». По условию Р(H1)=0.1; Р(H2)=0.4; Р(H3)=0.5 Условные вероятности того, что телевизор не потребует ремонта, если он поступил от поставщика: Р(А/H1)=0.7; Р(А/H2)=0.49; Р(А/H3)=0.8 По формуле полной вероятности: Р(А)= Р(H1) Р(А/H1)+ Р(H2) Р(А/H2)+ Р(H3) Р(А/H3)= 0,1*0,7+0,4*0,9+0,5*0,8=0,83. 2) найдем вероятности того, что телевизор не потребовал ремонта в течение гарантийного срока от первого, второго и третьего поставщиков. По формуле Байеса:
Таким образом, наивероятнейшей будет гипотеза о том, что телевизор потупил от третьего поставщика.
Формула Бернулли. В семье 5 детей. Найти вероятности того, что среди этих детей: 1) 4 мальчика; 2) не менее четырех мальчиков; 3) менее четырех мальчиков. Вероятность рождения мальчика равна 0,51. 1). Вероятность рождения мальчика равна 0,51, значит вероятность рождения девочки равна 0,49. Используем формулу Бернулли
2) 3) Формула Пуассона. На факультете 730 студентов. Какова вероятность того, что а) 1 сентября является днем рождения одновременно трех студентов факультета; б) хотя бы у одного день рождения 1 сентября; в) более трех человек имеют день рождения 1 сентября. Решение. а) Вероятность того, что день рождения студента будет 1 сентября p=1/365. Так как р – мало, а n- велико и
б) Р{хотя бы один день рождения 1 сентября}= 1- P{ни одного дня рождения 1 сентября}= 1- в) P{более трех дней рождения 1 сентября}= 1-P{не более трех дней рождения}= 1-( Локальная и интегральная теоремы Муавра-Лапласа. Контрольную работу по теории вероятностей с первого раза успешно выполняют 50% студентов. Найти вероятность того, что из 100 студентов работу успешно выполнят а) 45 студентов; б) от 45 до 65 студентов. Решение. а) по условию р=0,5. Так как n велико (npq=100*0.5*0.5=25³9), то применим локальную теорему Лапласа.
б)
К задачам 11-20.
Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x); 2) схематично построить графики функций f(x) и F(х); 4) найти вероятность того, что Х примет значение из интервала (
Решение. 1) плотность распределения случайной величины равна первой производной от функции распределения.
2) 3) Для нахождения математического ожидания используем формулу
4)
Приложение. Для вычисления интегралов используем формулы.
К задачам 21-30. Заданы математическое ожидание а=3 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х.
Решение. 1). Составим функцию плотности распределения случайной величины Х с параметрами а=3, s=5 воспользовавшись формулой
Построим график 2) Воспользуемся формулой:
Значения функций найдены по таблице приложений. 3) 4) Воспользуемся формулой К задачам 31-40. Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если генеральное среднее квадратическое отклонение s=5, выборочная средняя Решение. Требуется найти доверительный интервал Все величины, кроме t, известны. Найдем t из соотношения Ф(t)=0,95/2=0,475. По таблице приложения находим t=1,96. Подставив, окончательно получим искомый доверительный интервал 12,04<a<15,96. К задачам 41-50. Отдел технического контроля проверил 200 партий одинаковых изделий и получил следующее эмпирическое распределение, частота ni – количество партий, содержащих xi нестандартных изделий.требуется при уровне значимости 0,05 проверить гипотезу о том, что число нестандартных изделий Х распределено по закону Пуассона.
Решение. Найдем выборочную среднюю:
Примем в качестве оценки параметра l распределения Пуассона выборочную среднюю l=0,6. Следовательно, предполагаемый закон Пуассона Положив i=0,1,2,3,4 найдем вероятности Piпоявления i нестандартных изделий в 200 партиях: Найдем теоретические частоты по формуле Сравним эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого составим расчетную таблицу. Объединим малочисленные частоты(4+2=6) и соответствующие им теоретические частоты (3,96+0,6=4,56).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.56.125 (0.008 с.) |

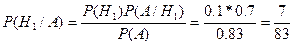

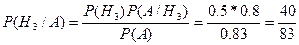
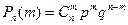



 то применима формула Пуассона.
то применима формула Пуассона.
 = 1-0,1353=0,8647.
= 1-0,1353=0,8647.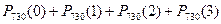 )=1-(0,1353+0,2707+0,2707+0,1805)=0,1428.
)=1-(0,1353+0,2707+0,2707+0,1805)=0,1428.
 .
. ).
).
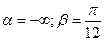
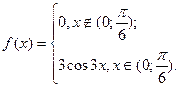
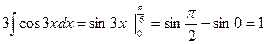 . Условие нормировки выполнено.
. Условие нормировки выполнено.
 , где a,b начало и конец интервала, где определена плотность.
, где a,b начало и конец интервала, где определена плотность. ;
;


 .
.

 . Построим схематически график функции
. Построим схематически график функции  . Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=3 и имеет max в этой точке, равный
. Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=3 и имеет max в этой точке, равный  , т.е.
, т.е.  и две точки перегиба
и две точки перегиба 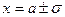 с ординатой
с ординатой 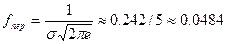




 . По условию вероятность попадания в интервал симметричный относительно математического ожидания
. По условию вероятность попадания в интервал симметричный относительно математического ожидания 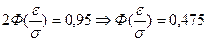 . По таблице найдем t, при котором Ф(t)=0,475, t=2. значит
. По таблице найдем t, при котором Ф(t)=0,475, t=2. значит  . Таким образом,
. Таким образом,  . Ответ хÎ(-1;7).
. Ответ хÎ(-1;7).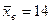 и объем выборки n=25.
и объем выборки n=25.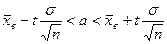 .
.
 имеет вид
имеет вид  .
.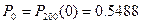 ,
,  ,
,  ,
,  ,
,  .
. . Подставив в эту формулу значения вероятности, получим
. Подставив в эту формулу значения вероятности, получим  ,
,  ,
,  ,
,  ,
, 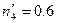 .
.
 )2
)2




