Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельные теоремы в схеме Бернулли.Содержание книги Поиск на нашем сайте
1. Предельная теорема Пуассона. При р»0, n-велико, np= l £ 10.
Формула дает распределение Пуасона, описывает редкие события.
2. Предельная теорема Муавра-Лапласа. 0 £ p £ 1, n –велико, np>10
3. Предельная интегральная теорема Муавра-Лапласа. В условиях предыдущей теоремы вероятность того, что событие А в серии из n испытаний наступит не менее k1 раз и не более k2 раз:
Следствие:
Случайная – величина, которая в ходе опыта принимает то или иное значение из возможных своих значений, меняющееся от опыта к опыту и зависящее от множества непредсказуемых факторов. Если случайные события характеризуют процесс качественно, то случайная величина – количественно. Случайная величина – численная функция, задаваемая на множестве элементарных событий. На одном множестве может быть несколько случайных величин. Дискретная случайная величина (ДСК) – величина, принимающая счетное (конечное или бесконечное) множество значений. Непрерывная случайная величина (НСВ) – случайная величина, значения которой образуют несчетные множества. (Например, расход бензина на 100 км у автомобиля Жигули в Нижнем Новгороде). Задать св – значит указать все множество ее значений и соответствующие этим значениям вероятности. Говорят, что задан закон распределения случайной величины. Случайная величина может быть задана несколькими способами: 1. Табличный.
Значения случайных величин в таблице ранжируются, т.е. указываются в порядке возрастания. Недостпаток табличного способа в том, что он пригоден только для случайных величин, принимающих небольшое количество значений.
2. Функция распределения F(x) = P(X<x) или интегральный закон распределения. Указывается вероятность того, что случайная величина принимает значение < x.
При увеличении значения случайной величины, количество ступенек функции F(х) возрастает, уменьшается их высота и в пределе при Свойства функции F(х). 1. Неотрицательна. 0£ F(х)£1 2. Неубывающая F(х2)> F(х1) при х2>х1 3. 4. Р(a<x<b) = F(a) – F(b) Вероятность того, что значение х попадет в интервал (а,b) определяется разностью значений функции на концах интервала.
Наряду с F(х) вводится f(x) - функция плотности вероятности или дифференциальный закон распределения:
Свойства функции f(x): 1. Неотрицательна. (т.к. F(x) неубывающая, f(x)³0) 2.
Основные дискретные и непрерывные случайные величины. Дискретные случайные величины (ДСВ). 1. Биноминальная случайная величина x{0,1,2,3…n}
2. Пуассоновская случайная величина x{0,1,2,3…}
3. Бернуллиевая случайная величина
4. Равномерное распределение
Непрерывные случайные величины (НСВ). 1. Равномерное распределение
2. Треугольное распределение Симпсона
l - интенсивность.
4.Нормальный закон распределения.
s=1, m=0 – нормальное стандартное распределение (m-мат. ожидание)
При фиксированном s и изменяющемся m, кривая двигается вдоль Ох, не изменяя формы. При фиксированном m и изменяющемся s (s1<s2<s3), кривая вытягивается вдоль оси ординат, но площадь фигуры под каждой кривой = 1.
Функция Лапласа: Исчерпывающие представления о СВ дает закон её распределения. Во многих задачах, особенно на заключительной стадии, возникает необходимость получить о величине некоторое суммарное представление: центры группирования СВ – среднее значение или математическое ожидание, разброс СВ относительно её центра группирования. Эти числовые характеристики в сжатой форме отражают существенные особенности изучаемого распределения.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.58 (0.009 с.) |

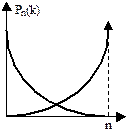
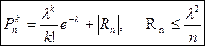
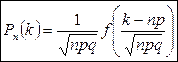
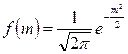 - стандартное нормальное распределение
- стандартное нормальное распределение
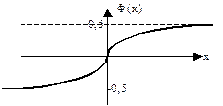
 - функция Лапласа
- функция Лапласа


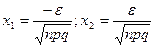
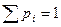
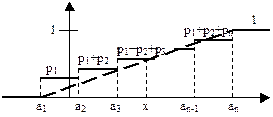
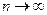 получаем гладкую непрерывную функцию F(х).
получаем гладкую непрерывную функцию F(х).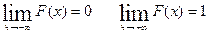
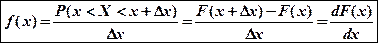
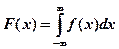
 Площадь фигуры под кривой на интервале (a,b) равна:
Площадь фигуры под кривой на интервале (a,b) равна: 
 - условие нормировки функции f(x).
- условие нормировки функции f(x).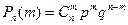 , p+q=1, 0<p<1
, p+q=1, 0<p<1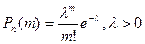
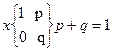
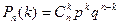
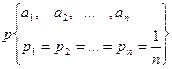
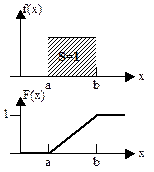


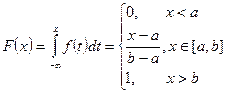



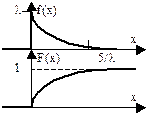 3. Экспоненциальное (показательное) распределение. Имеет важное значение в теории массового обслуживания и теории надежности.
3. Экспоненциальное (показательное) распределение. Имеет важное значение в теории массового обслуживания и теории надежности.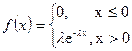
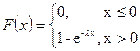

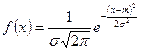 , s>0
, s>0 - такой подстановкой любое нормальное распределение приводится к стандартному.
- такой подстановкой любое нормальное распределение приводится к стандартному.