
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Элементы корреляционного и регрессионного анализа.Содержание книги
Поиск на нашем сайте
22. Функциональная, статистическая и корреляционная зависимости. Понятие регрессии. Линейная и нелинейная регрессия. Кривые регрессии их свойства. []. 23. Корреляционная таблица. Выборочный коэффициент корреляции. Методика его вычисления. Оценка тесноты связи. Выборочное корреляционное отношение, его свойства. Интервальное оценивание коэффициента корреляции и коэффициентов регрессии. []. 24. Линейная регрессия. Выборочные уравнения регрессии. Отыскание параметров выборочного уравнения прямой регрессии методом наименьших квадратов по несгруппированным и сгруппированным данным. []. Вопросы для самопроверки
1. Что называется статистической и корреляционной зависимостями? 2. Дайте определение выборочного коэффициента корреляции и перечислите его свойства. 3. Что называют линейной регрессией регрессией, множественной регрессией? 4. Что называется выборочным корреляционным отношением? Каковы достоинства и недостатки этой меры тесноты связи? 5. Как найти параметры выборочного уравнения прямой регрессии Y на X; Х на Y?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ Основные теоретические сведения Все события делятся на детерминированные, случайные и неопределенные. Если событие наступает в эксперименте всегда, оно называется достоверным, если никогда – невозможным. Это детерминированные события. Статистическое определение вероятности: Если в опыте, повторяющемся n раз, событие появляется mA раз, тогда относительная частота наступления события: Для достоверного события W: Р(W)=1. Для невозможного события Æ: Р(Æ)=0. 0 £ P(A) £ 1, т.к. 0£mA£n à 0 £ hn(A) £ 1 W mA=n hn(A)=1 Æ mA=0 hn(A)=0 Все мыслимые взаимоисключающие исходы опыта называются элементарными событиями. Наряду с ними можно наблюдать более сложные события – комбинации элементарных. Несколько событий в данном опыте называются равновозможными, если появление одного из них не более возможно, чем другого. Классическое определение вероятности: Если n-общее число элементарных событий и все они равновозможные, то вероятность события А:
где mA- число исходов, благоприятствующих появлению события А. Теория сложных событий позволяет по вероятностям простых событий определять вероятности сложных. Она базируется на теоремах сложения и умножения вероятностей. 1) Суммой (объединением) двух событий А и В называется новое событие А+В, заключающееся в проявлении хотя бы одного из этих событий. 2) Произведением (пересечением) двух событий А и В называется новое событие АВ, заключающееся в одновременном проявлении обоих событий. А*В=АВ, АА=А, АВА=АВ. 3) Событие А влечет за собой появление события В, если в результате наступления события А всякий раз наступает событие В. АÌВ А=В: АÌВ, ВÌА Два события называются несовместными, если появление одного из них исключает возможность появления другого. Если события несовместны, то АВ=Æ. События А1, А2, …Аn образуют полную группу событий в данном опыте, если они являются несовместными и одно из них обязательно происходит: AiAj=Æ (i¹j, i,j=1,2…n) A1+A2+…+An=W
А и Теорема сложения вероятностей.
Вероятность суммы несовместных событий равна сумме вероятностей событий: Р(А+В+С+…) = Р(А) + Р(В) + Р(С) +… Следствие. Если события A1+A2+…+An - полная группа событий, то сумма их вероятностей равна 1.
P(A+ Вероятность наступления двух совместных событий равна: Р(А+В) = Р(А) + Р(В) - Р(АВ)
Теорема умножения вероятностей. Условные вероятности. Опыт повторяется n раз, mB раз наступает событие В, mАВ раз наряду с событием В наступает событие А. hn(B) = Рассмотрим относительную частоту наступления события А, когда событие В уже наступило:
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

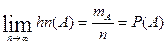 . Р(А) – вероятность наступления события А.
. Р(А) – вероятность наступления события А. ,
, -событие противоположное событию А, если оно состоит в непоявлении события А.
-событие противоположное событию А, если оно состоит в непоявлении события А.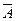 - полная группа событий, т.к. А+
- полная группа событий, т.к. А+ 
 hn(AB) =
hn(AB) = 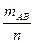
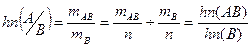
 - условная вероятность события А по событию В – вероятность события А, когда событие В уже наступило.
- условная вероятность события А по событию В – вероятность события А, когда событие В уже наступило.


