
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ДУ с разделяющимися переменными.Содержание книги
Поиск на нашем сайте
Уравнение в нормальной форме вида
называется ДУ с разделяющимися переменными. В дифференциальной форме ДУ с разделяющимися переменными имеет вид
Представляя
Далее разделим переменные, т.е. используя свойства пропорций, соберем слева функции, содержащие только переменную х, а справа – функции, содержащие переменную у:
Интегрируя обе части последнего равенства, получим общий интеграл ДУ:
Пример 9.1. Найти частное решение ДУ
удовлетворяющее начальному условию Решение. Заменим
Разделив переменные, получим уравнение Интегрируя обе части последнего уравнения, запишем общий интеграл ДУ:
Поскольку с – произвольная постоянная, то мы можем взять ее в логарифмическом виде, т.е. положить
Воспользовавшись свойством логарифмов,перепишем последнее ра-венство в виде Найдем частное решение этого уравнения, удовлетворяющее заданному начальному условию. Подставив в формулу общего решения х =1 и у = 2, найдем значение постоянной C:
Следовательно, искомое частное решение ДУ имеет вид Замечание. В этом примере и в дальнейшем мы используем следующие свойства логарифмов:
3. Пример 9.2. Найти общее решение ДУ
Решение. Заменим
Проинтегрируем обе части последнего уравнения:
Найдем интегралы:
Таким образом, мы получим решение ДУ в виде
где введено обозначение Воспользовавшись свойством логарифмов, находим общее решение исходного уравнения:
Однородное ДУ. Дифференциальное уравнение
Однородное ДУ сводится к ДУ с разделяющимися переменными с помощью подстановки
где Пример 9.3. Найти общее решение уравнения
Решение. О бозначив правую часть уравнения Следовательно, данное уравнение является однородным. Для решения этого уравнения применим подстановку Уравнение примет вид
Получили уравнение с разделяющимися переменными. Решая его, находим
Так как Линейное ДУ. Дифференциальное уравнение вида
где P(x), Q(x) – заданные функции, называется линейным ДУ относительно При решении линейного ДУ можно применить подстановку Бернулли
где Подставив формулы (9.6) в уравнение (9.5), получим
Группируем первый и третий члены уравнения и выносим v за скобки: Выбираем функцию u (x) таким образом, чтобы выражение в скобках обращалось в нуль. Таким образом, получаем систему:
Решая первое уравнение системы, находим одно из его частных решений u (x) (здесь полагаем с = 0). Подставляя затем u (x) во второе уравнение системы и решая его, находим функцию v (x). Пример 9.4. Решить дифференциальное уравнение Решение. Разделим обе части уравнения на x и перепишем его
Получим уравнение вида
где Подставим формулы (9.9) в уравнение (9.8):
Группируем первый и третий члены и выносим v за скобки:
Приравняем к нулю выражение, стоящее в скобках, и решаем систему уравнений Первое уравнение системы (9.10) является уравнением с разделяющимися переменными. Найдем одно из его решений:
Таким образом, получим общее решение исходного уравнения
Замечание. Уравнение вида
Уравнение Бернулли. Уравнением Бернулли называется ДУ вида
где Так же, как и линейное, уравнение Бернулли можно решать с помощью подстановки Пример 9.5. Найти общее решение ДУ Решение. Это уравнение Бернулли вида Сделаем подстановку
Уравнение примет вид
Приравняем выражение в скобках к нулю и решим систему уравнений:
Из первого уравнения системы, находим функцию
Подставив
Далее разделяем переменные и находим функцию
Значит, общее решение уравнения имеет вид
Пример 9.6. Определить тип ДУ 1-го порядка и указать метод его решения. а) Решение. а) В уравнении Это уравнение является уравнением с разделяющимися переменными. При его решении заменяем
б) В уравнении Разрешим уравнение относительно производной
Обозначим
Следовательно, уравнение является однородным ДУ. Для его решения применим подстановку
где u = u (x) – новая неизвестная функция. Кроме этого, уравнение
Уравнение (9.12)является уравнением Бернулли вида Это уравнение можно решать с помощью подстановки в) Разрешим уравнение
Уравнение (9.13)является линейным уравнением Это уравнение можно решать с помощью подстановки
где
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.125 (0.007 с.) |

 (9.2)
(9.2) .
.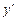 в виде
в виде  перепишем уравнение (9.2) следующим образом:
перепишем уравнение (9.2) следующим образом: .
. .
. .
. , (9.3)
, (9.3) .
. .
. .
. . (9.4)
. (9.4) . Тогда решение (9.4) примет вид
. Тогда решение (9.4) примет вид .
. , откуда
, откуда  – общее решение ДУ(9.3).
– общее решение ДУ(9.3).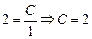 .
. .
. ;
; ;
; (n – действительное число).
(n – действительное число).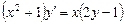 .
.




 , или
, или 
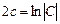 .
.
 , или
, или  .
. называется однородным, если функция f (x, y) удовлетворяет условию
называется однородным, если функция f (x, y) удовлетворяет условию , где t – параметр.
, где t – параметр. ,
, – новая неизвестная функция.
– новая неизвестная функция.
 , находим
, находим 
 .
. ,
,  , где
, где  ,
,  ,
, 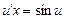 .
. ,
,  ,
, 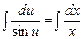 ,
, ,
, 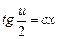 ,
,  .
. , то общее решение дифференциального уравнения имеет вид
, то общее решение дифференциального уравнения имеет вид  .
. , (9.5)
, (9.5)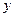 и
и  .
. ,
, , (9.6)
, (9.6) - новые неизвестные функции.
- новые неизвестные функции.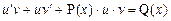 . 7)
. 7) .
.
 .
. . (9.8)
. (9.8)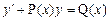 , где P(x)
, где P(x)  , Q(x)
, Q(x)  . Это линейное ДУ. Применим подстановку
. Это линейное ДУ. Применим подстановку , (9.9)
, (9.9)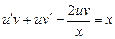 .
. .
. (9.10)
(9.10) ;
; 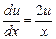 ;
;  ;
;  ;
; 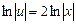 ;
;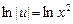 ,
,  . Подставляя
. Подставляя 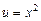 во второе уравнение системы (9.10), находим функцию v:
во второе уравнение системы (9.10), находим функцию v: ;
;  ;
;  .
. .
. называется линейным ДУ относительно х и х′. При его решении применяют подстановку:
называется линейным ДУ относительно х и х′. При его решении применяют подстановку: ,
,  .
. , (9.11)
, (9.11)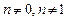 (при n = 0 уравнение (9.11) является линейным, а при n = 1 – уравнением с разделяющимися переменными).
(при n = 0 уравнение (9.11) является линейным, а при n = 1 – уравнением с разделяющимися переменными). .
.
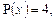

 .
.
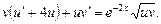

 :
:


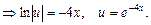
 в уравнение
в уравнение  получим уравнение
получим уравнение



 :
:
 .
.
 б)
б)  в)
в) 
 вынесем общие множители за скобки:
вынесем общие множители за скобки:  .
. разделяем переменные и интегрируем:
разделяем переменные и интегрируем: ,
,  ,
, .
.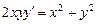 правая часть такова, что ее нельзя представить в виде произведения, а затем разделить переменные.
правая часть такова, что ее нельзя представить в виде произведения, а затем разделить переменные.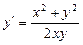 .
. . Находим
. Находим .
. ,
, или
или  , (9.12)
, (9.12) , где
, где 

 .
.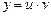 ,
,  , где
, где  – новые неизвестные функции.
– новые неизвестные функции. относительно производной и преобразуем его:
относительно производной и преобразуем его: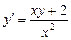 ,
,  ,
,  . (9.13)
. (9.13) , Q(x)
, Q(x)  .
. - новые неизвестные функции.
- новые неизвестные функции.


