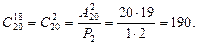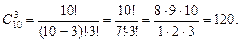Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о поверхностных интегралах.Содержание книги
Поиск на нашем сайте
Поток векторного поля Пусть функция Определение. Предел последовательности интегральных сумм Вычисление этого интеграла сводится к вычислению двойного интеграла (см.[7], §15.3). Пусть в каждой точке некоторой поверхности
Рис. 13.2 Зададим направление нормали Поверхностным интегралом второго рода от вектора
В теории поля поверхностный интеграл второго рода называется потоком векторного поля Примеры потоков векторных полей 1. Поток электрического поля точечного заряда напряженностью
2. Поток магнитного поля с индукцией
ЗАДАЧИ ДЛЯСАМОСТОЯТЕЛЬНОЙ РАБОТЫ 1. Дана функция 2. Задано векторное поле grad div 3. Выяснить, является ли векторное поле 4. Найти циркуляцию векторного поля КОНТРОЛЬНЫЙ ТЕСТ ПО МОДУЛЮ №13
Модуль 14. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Классификация событий Определение. Событием в теории вероятностей называется всякий факт, который может произойти или не произойти в результате какого-то опыта (испытания). Например, трактор проработал без капитального ремонта 7000 часов - это событие. В теории вероятностей события обозначаются заглавными буквами латинского алфавита: А, В, С и т.д. или одной буквой, снабженной индексами: По возможности появления события делятся на достоверные, невозможные, случайные. Определение. Достоверное событие - это такое событие, которое в результате данного испытания обязательно наступит. Например, если в ящике находятся только болты, то событие “из ящика извлечен болт” является достоверным. Определение .Невозможное событие - это такое событие, которое в результате данного испытания не может произойти. Извлечение из массы непротравленного зерна одного протравленного зерна - событие невозможное. Определение. Случайное событие - это такое событие, которое в результате данного испытания может произойти, но может и не произойти. Например, на колхозном поле работают 3 комбайна. Событие состоящее в том, что в данный момент неисправными окажутся все комбайны – случайное. Виды случайных событий. События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. Например, механизатор может работать на тракторе и на комбайне. Пусть событие А - механизатор в данный момент работает на тракторе, событие В - на комбайне. События А и В - несовместные. События Несколько событий образуют полную группу, если в результате испытания обязательно наступит хотя бы одно из них. На практике широкое применение находит полная группа несовместных событий. Например, по цели производится три выстрела. Исходом испытания может быть одно из событий: А – три промаха, В – одно попадание, С – два попадания, D – три попадания. События А, В, С, D образуют полную группу несовместных событий. Два несовместных события, образующих полную группу, называются противоположными. Событие, противоположное событию А, принято обозначать Например, событие А - деталь годная, событие Элементы комбинаторики Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используют при непосредственном вычислении вероятностей. Соединениями называют различные группы, составленные из каких-либо объектов. Элементами называются объекты, из которых составлены соединения. Различают следующие три вида соединений: перестановки, размещения и сочетания. Определение. Перестановками из Число перестановок из
Пример 14.1. Сколькими различными способами могут разместиться на скамейке 6 человек? Решение. Количество таких способов вычисляется по формуле:
Определение. Размещениями из Число размещений из
Пример14.2. На станции имеется 6 запасных путей. Сколькими способами можно расставить на них 4 поезда? Решение. Число способов вычисляется по формуле:
Определение. Сочетаниями из Число сочетаний из
Для упрощения вычислений при
Пример14.3. Бригадир должен отправить на работу звено из 18 человек. Сколько таких звеньев можно составить из 20 человек бригады? Решение. Число звеньев определяется по формуле:
Пример 14.4. Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов? Решение. В соответствии с формулой находим
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.61 (0.007 с.) |

 определена и непрерывна в каждой точке некоторой поверхности
определена и непрерывна в каждой точке некоторой поверхности  . Разобьем
. Разобьем  элементарных частей
элементарных частей  с площадями
с площадями 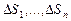 . На каждой элементарной поверхности
. На каждой элементарной поверхности  выберем произвольную точку
выберем произвольную точку 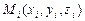 и составим сумму
и составим сумму 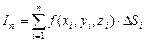 .
.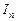 , когда
, когда 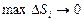 называется поверхностным интегралом первого рода от функции
называется поверхностным интегралом первого рода от функции  .
.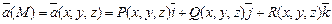 .
.

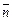 к поверхности
к поверхности 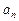 вектора
вектора  в каждой точке
в каждой точке 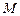 поверхности
поверхности 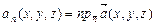 будет скалярной функцией и от нее можно вычислить поверхностный интеграл первого рода.
будет скалярной функцией и от нее можно вычислить поверхностный интеграл первого рода. по поверхности
по поверхности  этого вектора на вектор нормали
этого вектора на вектор нормали  к
к 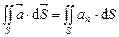 .
.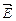 через замкнутую поверхность
через замкнутую поверхность 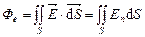 .
. через поверхность
через поверхность  .
.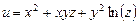 и точки
и точки 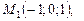
 . Найти: а)
. Найти: а) 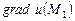 ; б) производную в точке
; б) производную в точке 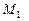 по направлению вектора
по направлению вектора 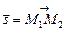 .
. . Найти div
. Найти div 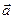 и
и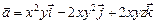 гармоническим.
гармоническим.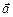 вдоль контура эллипса
вдоль контура эллипса 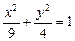 при положительном направлении обхода.
при положительном направлении обхода.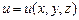 – скалярное поле, то равенство
– скалярное поле, то равенство  задает
а)ротор; б)дивергенцию;
в)градиент;г)производную по направлению.
задает
а)ротор; б)дивергенцию;
в)градиент;г)производную по направлению.
 во всех точках которого выполняется условие
во всех точках которого выполняется условие  , называется
а)гармоническим;б)скалярным;
в)соленоидальным; г)потенциальным.
, называется
а)гармоническим;б)скалярным;
в)соленоидальным; г)потенциальным.
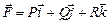 , то циркуляция силы
, то циркуляция силы  вдоль замкнутой линии L представляет собой:
а) мощность; б) работу силы;
в) момент силы; г) плечо силы.
вдоль замкнутой линии L представляет собой:
а) мощность; б) работу силы;
в) момент силы; г) плечо силы.
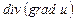 есть
а)скалярное поле; б)векторное поле;
в)скалярно-векторное поле; г)оператор не определен.
есть
а)скалярное поле; б)векторное поле;
в)скалярно-векторное поле; г)оператор не определен.
 находится по формуле
находится по формуле
 ; б)
; б) 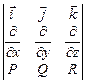 ;
;
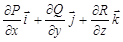 ;г)
;г) 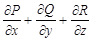 .
.
 по направлению вектора
по направлению вектора 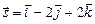 в точке
в точке 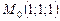 равна
а)
равна
а)  ; б)
; б) 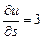 ; в)
; в) 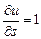 ; г)
; г) 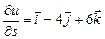 .
.
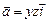 то
то 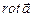 равен.
а)
равен.
а) 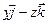 ; б)0; в)
; б)0; в) 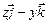 ; г)
; г) 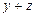 .
.
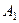 ,
, 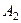 ,
, 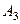 и т.д.
и т.д.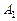 ,
,  ,…
,…  называются равновозможными, если условия их появления одинаковы.
называются равновозможными, если условия их появления одинаковы. .
. - деталь бракованная.
- деталь бракованная.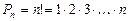 .
. .
. в каждом
в каждом  называют такие соединения, в каждое из которых входит
называют такие соединения, в каждое из которых входит 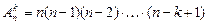
 .
. или
или 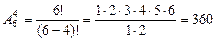 .
.
 .
. полезно использовать следующее свойство сочетаний:
полезно использовать следующее свойство сочетаний: .
.