
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы распределенияСодержание книги
Поиск на нашем сайте
Биномиальный закон. Случайная величина
где Числовые характеристики биномиального закона распределения:
Закон Пуассона. Дискретная случайная величина
где Числовые характеристики закона Пуассона:
Определение. Интенсивностью потока
Пример 14.21. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 5 минут поступит 3 вызова. Решение. По условию задачи
Равномерное распределение. Непрерывная случайная величина называется равномерно распределенной в интервале
Числовые характеристики равномерного закона распределения:
График дифференциальной функции равномерного распределения приведен на рис. 14.4.
Нормальное распределение. Непрерывная случайная величина называется нормально распределенной, если ее плотность распределения равна
где
График дифференциальной функции
Вероятность того, что нормально распределенная случайная величина
где Для нормального закона распределения верна следующая формула:
Показательное распределение. Показательным называется распределение, дифференциальная функция которого имеет вид
где График дифференциальной функции показательного распределения приведен на рис. 14.6.
Числовые характеристики показательного распределения:
Интегральная функция для показательного распределения имеет вид Функция надежности Показательное распределениешироко применяетсяв теории надежности. Пусть
Определение. Функцией надежности
Для показательного закона распределения вероятность безотказной работы элемента за время
Пример 14.22. Испытывают два независимо работающих элемента. Длительности безотказной работы элементов равны
Найти вероятность того, что за время длительностью 6 часов 1) оба элемента откажут, 2) оба элемента не откажут, 3) откажет хотя бы один элемент. Решение. Рассмотрим случайные величины:
Находим вероятности отказов элементов:
Найдем вероятности следующих событий. 1. Событие А – оба элемента откажут имеет вероятность
2. Событие В – оба элемента не откажут имеет вероятность
3. Событие С – хотя бы один элемент откажет имеет вероятность
Пример 14.23. Станок – автомат изготовляет шарики для подшипника. Шарик считается годным, если отклонение Решение. Воспользуемся формулой
где По условию задачи
Таким образом, станок-автомат изготавливает 92,8% годных шариков.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.249 (0.008 с.) |

 называется распределенной по биномиальному закону, если она принимает конечное множество значений 0, 1, 2, …
называется распределенной по биномиальному закону, если она принимает конечное множество значений 0, 1, 2, … 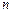 , а вероятность того, что
, а вероятность того, что  , выражается формулой:
, выражается формулой: ,
, - вероятность наступления события А при одном испытании,
- вероятность наступления события А при одном испытании,  .
. ,
,  .
.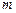 , …, а вероятность того, что
, …, а вероятность того, что 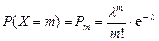 ,
, – параметр закона Пуассона.
– параметр закона Пуассона. ,
, 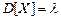 .
. называют среднее число событий, которые появляются в единицу времени. Доказано, что если известна постоянная интенсивность потока
называют среднее число событий, которые появляются в единицу времени. Доказано, что если известна постоянная интенсивность потока  событий за время длительностью
событий за время длительностью 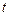 определяется формулой:
определяется формулой: .
. Тогда
Тогда
 , если ее плотность распределения в этом интервале постоянна, а вне его равна нулю:
, если ее плотность распределения в этом интервале постоянна, а вне его равна нулю:

 ,
,  .
.

 ,
, - среднее квадратическое отклонение.
- среднее квадратическое отклонение.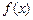 нормального закона распределения (нормальная кривая или кривая Гаусса) имеет вид
нормального закона распределения (нормальная кривая или кривая Гаусса) имеет вид

 , выражается формулой:
, выражается формулой: ,
, .
. .
.
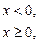
 – параметр показательного распределения.
– параметр показательного распределения.

 ,
,  .
. .
. – продолжительность безотказной работы прибора. Функция распределения случайной величины Т выражает вероятность отказа за время t:
– продолжительность безотказной работы прибора. Функция распределения случайной величины Т выражает вероятность отказа за время t: .
. называют функцию, определяющую вероятность безотказной работы элемента за время длительностью
называют функцию, определяющую вероятность безотказной работы элемента за время длительностью  .
. вычисляется по формуле:
вычисляется по формуле: , где
, где  - интенсивность отказов.
- интенсивность отказов. .
. - время безотказной работы 1-го элемента.
- время безотказной работы 1-го элемента.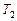 - время безотказной работы 2-го элемента.
- время безотказной работы 2-го элемента.

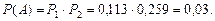

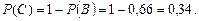
 его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина
его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина  мм, найти, сколькопроцентов годныхшариков изготавливает станок-автомат.
мм, найти, сколькопроцентов годныхшариков изготавливает станок-автомат. – функция интегральной теоремы Лапласа.
– функция интегральной теоремы Лапласа. ,
,  , поэтому
, поэтому
 .
.


