
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обыкновенные дифференциальныеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения второго порядка Дифференциальным уравнением второго порядка называется уравнение вида
где х – независимая переменная, у – неизвестная функция, а у′, у′′ - первая и вторая производные этой функции. Если уравнение (9.14) разрешимо относительно у′′, то его можно записать в виде
Общим решением ДУ 2-го порядка называется функция Решение, которое получается из общего решения при фиксированных значениях постоянных Задача Коши для ДУ 2-го порядка: найти частное решение ДУ (9.14), удовлетворяющее начальным условиям Геометрически задача Коши означает, что из множества интегральных кривых выбирается та, которая проходит через точку (х0;у0) и имеет в этой точке угловой коэффициент касательной Теорема Коши (о существовании и единственности решения задачи Коши для ДУ 2-го порядка).Если в ДУ Дифференциальные уравнения второго порядка, допускающие понижения порядка Рассмотрим некоторые частные случаи дифференциальных уравнений второго порядка 1. ДУ второго порядка, не содержащие явно y и y′. Рассмотрим уравнение
Последовательно дважды интегрируя обе части уравнения (9.16), находим общее решение ДУ
Пример 9.7. Найти частное решение ДУ Решение. Дважды интегрируя, находим
Используя начальные условия, найдем частное решение уравнения
Следовательно, искомое частное решение имеет вид
ДУ второго порядка, не содержащие явно функцию y. Рассмотрим уравнение
Применяя подстановку
получим дифференциальное уравнение первого порядка вида
Решив это уравнение, найдем функцию Затем решаем уравнение первого порядка с разделяющимися переменными
из которого находим искомую функцию Пример 9.8. Найти частное решение ДУ Решение. Это неполное уравнение второго порядка, не содержащее явно искомую функцию y. Порядок этого уравнения можно понизить, положив
Разделим переменные и найдем функцию
Возвращаясь к переменной у, получим уравнение первого порядка
Прежде чем интегрировать это уравнение, целесообразно определить значение постоянной Подставляя
Наконец, используя начальные условия Получаем искомое частное решение: Замечание. При отыскании частных решений уравнений высших порядков нет необходимости сначала находить общее решение, а лишь затем определять значение всех постоянных. Лучше определять значения каждой постоянной немедленно после того, как она появляется в процессе решения.
ДУ второго порядка, не содержащие явно независимую переменную. При решении уравнения вида
применяем подстановку
Получим дифференциальное уравнение первого порядка:
Найдем общее решение этого уравнения Пример 9.9. Найти частное решение уравнения Решение. Данное уравнение второго порядка не содержит явно независимую переменную. Применим подстановку Тогда
Если приравнять нулю первый множитель, то получаем: Приравняем к нулю второй множитель:
Используя начальные условия
Далее решаем уравнение
Теперь определим значение
Тогда
откуда получаем искомое частное решение
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 970; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.134 (0.008 с.) |

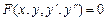 , (9.14)
, (9.14)
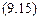
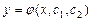 , которая при любых значениях постоянных
, которая при любых значениях постоянных  является решением этого уравнения.
является решением этого уравнения.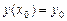 ,
,  .
. .
.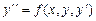 функция
функция  и ее частные производные
и ее частные производные  непрерывны в некоторой области D пространства, то для любой точки
непрерывны в некоторой области D пространства, то для любой точки 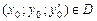 существует единственное решение у (х) этого уравнения, удовлетворяющее начальным условиям
существует единственное решение у (х) этого уравнения, удовлетворяющее начальным условиям 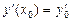 .
. . (9.16)
. (9.16)
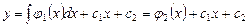 .
.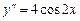 , удовлетворяющее начальным условиям у (0) = 1, у′ (0) = 1.
, удовлетворяющее начальным условиям у (0) = 1, у′ (0) = 1.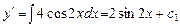 ,
,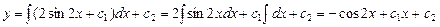 Таким образом, получим общее решение ДУ:
Таким образом, получим общее решение ДУ: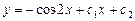 .
.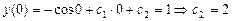 ,
,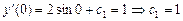 .
.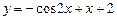 .
.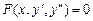 . (9.17)
. (9.17)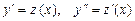 ,
,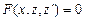 .
.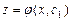 – общее решение.
– общее решение.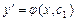 ,
,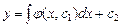 .
. , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 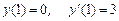 .
.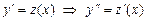 . Уравнение после подстановки примет вид:
. Уравнение после подстановки примет вид: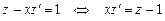 .
.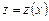 :
: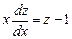 ,
,  ,
,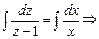

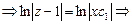
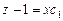
 .
.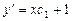 .
. , используя заданные начальные условия
, используя заданные начальные условия 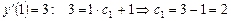 .
. в уравнение
в уравнение  , получимуравнение
, получимуравнение 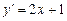 , откуда находим
, откуда находим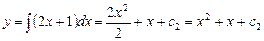 .
. , определим
, определим 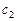 :
: 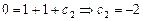 .
. .
. (9.18)
(9.18)
 . (9.19)
. (9.19)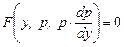 .
.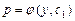 и подставим
и подставим  . Затем решаем уравнение первого порядка с разделяющимися переменными
. Затем решаем уравнение первого порядка с разделяющимися переменными 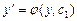 , из которого находим искомую функцию:
, из которого находим искомую функцию:  .
.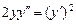 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 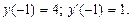
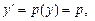 где
где  – новая неизвестная функция переменной
– новая неизвестная функция переменной 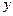 .
.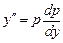 и уравнение примет вид
и уравнение примет вид
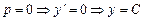 . Но это решение не удовлетворяет начальному условию
. Но это решение не удовлетворяет начальному условию  , а значит является посторонним.
, а значит является посторонним.
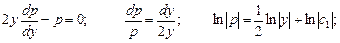
 или
или 
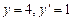 при
при 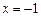 , находим
, находим  :
: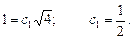
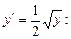
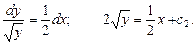
 из условия y = 4 при
из условия y = 4 при 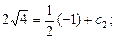

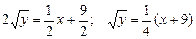 ,
, .
.


