
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа № 4. «Дифференциальные уравнения. Ряды».Содержание книги
Поиск на нашем сайте 1. Найти общее решение линейного дифференциального уравнения и частное решение, удовлетворяющее начальному условию y (x 0) = y 0. 1. 3. 5. 7. 9. 2. Найти общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида и частное решение, удовлетворяющее начальным условиям y (x 0) = y 0 и 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 3. Написать три первых члена степенного ряда, найти его область абсолютной сходимости. 1. 4. 7. 10. 4. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд. 1. 4. 7. 10. Основные теоретические сведения. Дифференциальные уравнения 1. Равенство вида 2. Натуральное число n, являющееся порядком старшей производной, называется порядком дифференциального уравнения. 3. Дифференциальным уравнением 1-го порядка называется уравнение вида 4. Решением дифференциального уравнения 1-го порядка называется функция y = j(x), имеющая непрерывную производную 5. Задача Коши для дифференциального уравнения 1-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальному условию y = y 0 при x = x 0. 6. Общим решением дифференциального уравнения 1-го порядка называется функция y = j(x; С), содержащая произвольную постоянную С и удовлетворяющая условиям: 1) при любых начальных условиях (x 0; y 0) уравнение y 0 = j(x 0; С) должно быть разрешимо относительно С так, что С = y(x 0; y 0); 2) при всех значениях постоянной С = y(x 0; y 0) функция y = j(x; y(x 0; y 0)) должна удовлетворять дифференциальному уравнению. 7. Всякое решение, получаемое из общего при фиксированном значении постоянной С называется частным решением дифференциального уравнения. 8. Уравнение вида 9. Уравнение вида 10. Уравнение вида 11. Уравнение вида 12. Дифференциальным уравнением 2-го порядка называется уравнение вида 13. Решением дифференциального уравнения 2-го порядка называется функция y = j(x), имеющая непрерывные производные 14. Задача Коши для дифференциального уравнения 2-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальным условиям y = y 0, 15. Общим решением дифференциального уравнения 2-го порядка называется функция y = j(x; С 1; С 2), содержащая две произвольные постоянные С 1, С 2 и удовлетворяющая условиям: 1) при любых начальных условиях 16. Всякое решение, получаемое из общего при фиксированных значениях постоянных С 1, С 2 называется частным решением дифференциального уравнения. 17. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка: а) б) в) 18. Линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами называется уравнение вида Если Если Если 19. Линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами с правой частью специального вида называется уравнение вида Если Если Ряды Числовые ряды Основные понятия 1. Пусть дана бесконечная последовательность чисел а 1, а 2, …, аn. Числовым рядом называется сумма вида 2. Если существует конечный предел 3. Основные свойства сходящихся числовых рядов: а) Необходимый признак сходимости: если числовой ряд б) Достаточное условие расходимости: если в) Если все члены сходящегося числового ряда г) Если два сходящихся числовых ряда Положительные числовые ряды 4. Первый признак сравнения рядов. Пусть даны два положительных ряда 1) из сходимости ряда 2) из расходимости ряда 5. Второй признак сравнения рядов. Пусть даны два положительных ряда 6. При использовании признаков сравнения чаще всего используют эталонные ряды: 1) Геометрический ряд a + aq + aq 2 + … + aqn – 1 + … = 2) Ряд Дирихле 3) Частный случай ряда Дирихле при p = 1 – гармонический ряд 7. Признак Даламбера. Пусть дан положительный ряд 1) если 2) если 3) если 8. Радикальный признак Коши. Пусть дан положительный ряд 1) если 2) если 3) если 9. Интегральный признак Коши. Пусть дан положительный ряд
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

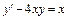 ,
,  . 2.
. 2.  ,
,  .
. , y (0) = 5. 4.
, y (0) = 5. 4.  , y (–2) = 5.
, y (–2) = 5.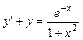 , y (0) = 2. 6.
, y (0) = 2. 6. 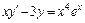 , y (1) = e.
, y (1) = e. , y (3) = 1. 8.
, y (3) = 1. 8.  , y (0) = 2.
, y (0) = 2. , y (1) = 0. 10.
, y (1) = 0. 10. 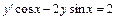 , y (0) = 3.
, y (0) = 3.
 , y (0) = –2,
, y (0) = –2,  .
.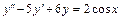 , y (0) = 3,
, y (0) = 3, 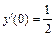 .
. , y (0) = –3,
, y (0) = –3,  .
. , y (0) = –1,
, y (0) = –1,  .
. , y (0) = 1,
, y (0) = 1,  .
. , y (0) = 2,
, y (0) = 2,  .
. , y (0) = 2,
, y (0) = 2,  .
. , y (0) = 3,
, y (0) = 3,  .
. , y (0) = 0,
, y (0) = 0,  .
. , y (0) = 0,
, y (0) = 0,  .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6. 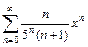 .
. . 8.
. 8.  . 9.
. 9.  .
.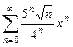 .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
. . 8.
. 8.  . 9.
. 9. 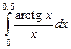 .
.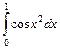 .
. , содержащее независимую переменную x, искомую функцию y = y (x) и ее производные какого-либо порядка, называется дифференциальным уравнением.
, содержащее независимую переменную x, искомую функцию y = y (x) и ее производные какого-либо порядка, называется дифференциальным уравнением. или в дифференциалах
или в дифференциалах  . Если эти равенства можно разрешить относительно производной, то их записывают в виде
. Если эти равенства можно разрешить относительно производной, то их записывают в виде  или
или  .
. на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство. или
или  называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду
называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду  или
или  путем разделения переменных x и y и затем почленно интегрируются.
путем разделения переменных x и y и затем почленно интегрируются. называется однородным дифференциальным уравнением. Используется замена:
называется однородным дифференциальным уравнением. Используется замена: 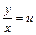 или
или  , где
, где  – новая неизвестная функция, тогда
– новая неизвестная функция, тогда  . Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле
. Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле  называется линейным дифференциальным уравнением. Используется метод Бернулли:
называется линейным дифференциальным уравнением. Используется метод Бернулли:  , где
, где  – новые неизвестные функции, тогда
– новые неизвестные функции, тогда  . Получаем:
. Получаем:  или
или  . Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем
. Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем  Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле
Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле  , где
, где  называется дифференциальным уравнением Бернулли. Используется метод Бернулли:
называется дифференциальным уравнением Бернулли. Используется метод Бернулли:  . Если уравнение можно разрешить относительно
. Если уравнение можно разрешить относительно 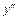 , то его записывают в виде
, то его записывают в виде  .
. на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство. при x = x 0.
при x = x 0. система уравнений
система уравнений  должна быть разрешима относительно постоянных С 1, С 2 так, что
должна быть разрешима относительно постоянных С 1, С 2 так, что  2) при всех значениях этих постоянных С 1, С 2 функция y = j(x; C 1; C 2) обращает дифференциальное уравнение в верное числовое равенство.
2) при всех значениях этих постоянных С 1, С 2 функция y = j(x; C 1; C 2) обращает дифференциальное уравнение в верное числовое равенство.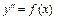 решается повторным интегрированием.
решается повторным интегрированием. , явно не содержащее искомой функции
, явно не содержащее искомой функции  . Используется замена:
. Используется замена:  , где
, где  – новая неизвестная функция, тогда
– новая неизвестная функция, тогда  . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу  , явно не содержащее независимой переменной
, явно не содержащее независимой переменной  . Замена:
. Замена:  , тогда
, тогда  . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу  . Составляется характеристическое уравнение
. Составляется характеристическое уравнение  .
. , то
, то  и общее решение исходного уравнения имеет вид:
и общее решение исходного уравнения имеет вид:  .
. , то
, то  и
и  .
. , то
, то  и
и  .
. . Его общее решение ищется в виде
. Его общее решение ищется в виде  , где
, где  – общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:
– общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:  – какое-либо частное решение исходного уравнения.
– какое-либо частное решение исходного уравнения. , где a – некоторое число, Pn (x) – многочлен степени n, то
, где a – некоторое число, Pn (x) – многочлен степени n, то 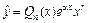 , где
, где  – многочлен степени
– многочлен степени  с неопределенными коэффициентами,
с неопределенными коэффициентами,  – число, равное кратности a как корня характеристического уравнения
– число, равное кратности a как корня характеристического уравнения  , где a, b – некоторые числа, Pn (x), Qm (x) – многочлены степени n и m соответственно, то
, где a, b – некоторые числа, Pn (x), Qm (x) – многочлены степени n и m соответственно, то  , где
, где 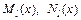 – многочлены степени
– многочлены степени  с неопределенными коэффициентами,
с неопределенными коэффициентами,  ,
,  как корня характеристического уравнения
как корня характеристического уравнения  .
. частичной суммы
частичной суммы  , то соответствующий числовой ряд
, то соответствующий числовой ряд  называется сходящимся и его сумма равна S. В противном случае числовой ряд называется расходящимся.
называется сходящимся и его сумма равна S. В противном случае числовой ряд называется расходящимся. .
. , то числовой ряд
, то числовой ряд 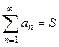 умножить или разделить на число
умножить или разделить на число  , то получится сходящийся ряд
, то получится сходящийся ряд  .
. почленно сложить (или вычесть), то получатся сходящиеся ряды
почленно сложить (или вычесть), то получатся сходящиеся ряды  (или
(или  ).
). . Если, начиная с некоторого номера n, выполняется условие
. Если, начиная с некоторого номера n, выполняется условие  , то:
, то: , то оба ряда ведут себя одинаково.
, то оба ряда ведут себя одинаково. сходится при
сходится при 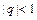 и расходится при
и расходится при  .
. сходится при
сходится при  и расходится при
и расходится при  .
. расходится.
расходится. . Тогда:
. Тогда: , то ряд сходится;
, то ряд сходится; , то ряд расходится;
, то ряд расходится; , то вопрос о сходимости ряда остается открытым.
, то вопрос о сходимости ряда остается открытым. . Тогда:
. Тогда: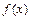 на
на  такая, что
такая, что  , то ряд и несобственный интеграл
, то ряд и несобственный интеграл  ведут себя одинаково.
ведут себя одинаково.


