
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец решения контрольной работы № 5.Содержание книги
Поиск на нашем сайте
Задание 1. На заочном отделении 80% всех студентов работают по специальности. Какова вероятность того, что из трёх отобранных случайным образом студентов по специальности работают: а) один; б) два; в) все; г) никто; д) хотя бы один студент? Решение. Вероятность выбрать студента, работающего по специальности, равна p = 0,8, а вероятность выбрать неработающего студента равна q = 1 – p = 0,2. Так как отбирают 3 студентов, то n = 3. а) Пусть событие А – «среди 3-х отобранных студентов только один работает по специальности», тогда вероятность этого события по формуле Бернулли равна б) По формуле Бернулли вероятность события В – «среди 3-х отобранных студентов два студента работают по специальности» равна в) Вероятность события С – «все трое отобранные студенты работают по специальности» равна г) Событие D – среди 3-х отобранных студентов никто не работает по специальности имеет вероятность д) Вероятность события Е – среди 3-х отобранных студентов работает по специальности хотя бы один студент вычислим по формуле Ответ: а) 0,096; б) 0,384; в) 0,512; г) 0,008; д) 0,992. Задание 2. Электролампы изготавливают на трех заводах. Первый завод производит 35 % общего количества электроламп, второй – 50 % и третий – 15 %. Продукция первого завода содержит 70 % стандартных ламп, второго – 80 % и третьего – 90 %. В магазин поступает продукция всех трех заводов. Какова вероятность того, что а) наудачу взятая лампа является стандартной; б) стандартная электролампа изготовлена на втором заводе? Решение. Пусть событие А – купленная в магазине лампа является стандартной. Введем гипотезы: Н 1 – наудачу взятая лампа изготовлена на первом заводе, Н 2 – наудачу взятая лампа изготовлена на втором заводе и Н 3 – наудачу взятая лампа изготовлена на третьем заводе. Вероятности гипотез по условию равны: P (H 1)=0,35, P (H 2)=0,5 и P (H 3)=0,15. События Н 1, Н 2, Н 3 являются несовместимыми и образуют полную группу, сумма их вероятностей равна единице: 0,35+0,5+0,15=1. Из условия следует, что а) Согласно формулы полной вероятности, вероятность искомого события А равна б) Переоценим гипотезу Н 2 по формуле Байеса после того, как стало известно, что событие А произошло:
Ответ: а) 0,78; б) Задание 3. Каждый из трех клиентов, взявший кредит в банке, может вернуть его раньше срока с вероятностью 0,4. 1) Составить закон распределения дискретной случайной величины Х – числа клиентов, вернувших кредит в банк раньше срока; 2) построить многоугольник распределения вероятностей; 3) найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х. Решение. Испытание состоит в попытке возвращения кредита раньше срока. В испытании может произойти или не произойти событие А – возвращение кредита раньше срока. Вероятность наступления события А равна P (A) = 0,4, тогда вероятность не наступления этого события равна q = 1 – 0,4 = 0,6. Рассматриваемая случайная величина Х в результате испытания может принять одно из следующих значений: 0, 1, 2 или 3. Вероятности этих значений вычислим по формуле Бернулли:
1) Таким образом, случайная величина Х имеет следующий закон распределения вероятностей:
Контроль: 0,216 + 0,432 + 0,288 + 0,064 = 1.
3) Определим математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х: М (Х) = np = 3×0,4 = 1,2; D (X) = npq = 3×0,4×0,6 = 0,72;
Задание 4. Непрерывная случайная величина X задана функцией распределения Решение. 1) Воспользуемся определением дифференциальной функции. При x £ 0 и при x > 2 имеем 2) Найдем числовые характеристики случайной величины Х. Математическое ожидание равно: Дисперсия равна Среднее квадратическое отклонение равно 3) Строим графики функций F (x) и f (х):
Ответ: 1) 5. Задана плотность распределения непрерывной случайной величины Х: Решение. Для определения неизвестного коэффициента С воспользуемся свойством плотности распределения вероятности
Ответ: С = 7. Список литературы 1. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. Ч. I, II: Учеб. пособие для студентов вузов. – М.: Высшая школа, 1982. 2. Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике. 2 курс / Под ред. С.Н. Федина. – М.: Айрис-пресс, 2004. – 592 с. 3. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс – М.: Рольф, 2001. – 576 с. 4. Математика: Программа, методические указания по самостоятельной работе и контрольные задания / Сост. В.А. Меркулов, А.Е. Меркулова. – Волжский: ВолжскИСИ, 1996. – 29 с. 5. Меркулов В.А. Курс высшей математики. Избранные разделы. Учеб. пособие / ВолгГАСУ. – Волгоград, 2004.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.194.165 (0.006 с.) |

 .
.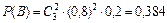 .
.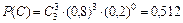 .
.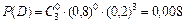 .
.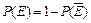 , где противоположное событие
, где противоположное событие  – никто из 3-х отобранных студентов не работает по специальности. Так как
– никто из 3-х отобранных студентов не работает по специальности. Так как 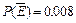 (см. г)), то получим
(см. г)), то получим  .
.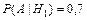 ,
, 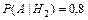 и
и 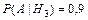 .
.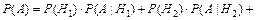
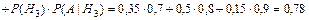 .
.
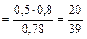 .
.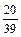 .
. ;
;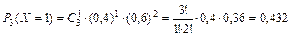 ;
; ;
; .
.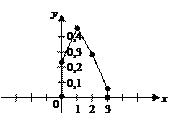 2) Строим многоугольник распределения вероятностей.
2) Строим многоугольник распределения вероятностей. .
.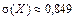 .
. Найти: 1) плотность распределения f (х); 2) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X; 3) построить графики функций F (x) и f (х).
Найти: 1) плотность распределения f (х); 2) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X; 3) построить графики функций F (x) и f (х).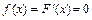 . При 0 < x £ 2
. При 0 < x £ 2  . Таким образом, величина Х имеет следующую дифференциальную функцию:
. Таким образом, величина Х имеет следующую дифференциальную функцию: 
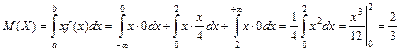 .
.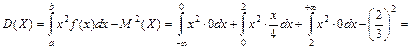
 .
.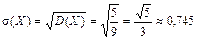 .
.
 2)
2)  ,
, 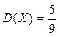 ,
, 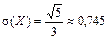 .
.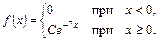 Найти неизвестный параметр С.
Найти неизвестный параметр С. :
: 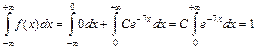 , откуда
, откуда 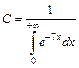 . Так как
. Так как 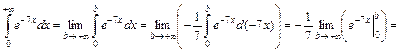
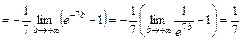 , то
, то 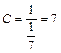 .
.


