
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заочной и ускоренной форм обученияСодержание книги
Поиск на нашем сайте
Методические указания для студентов экономической специальности Заочной и ускоренной форм обучения
Волжский, 2010 год Абрамов Е.В., Илларионова Е.Д., Волченко Е.Ю.
Данная работа охватывает курс высшей математики, читаемый студентам экономических специальностей на заочной и ускоренной формах обучения инженерных вузов. Методические указания содержат программу курса, указания по самостоятельной работе, основные теоретические сведения, контрольные работ и образцы их решения. Материалы будут полезны, прежде всего, студентам экономических специальностей заочной и ускоренной форм обучения инженерных вузов при организации самостоятельной работы и выполнении контрольных работ по математике.
ã Государственное образовательное учреждение высшего профессионального образования «Волгоградский государственный архитектурно-строительный университет», 2010
ã Волжский институт строительства и технологий (филиал) ВолгГАСУ, 2010
Содержание
Часть 1. ПРОГРАММА КУРСА Элементы векторной алгебры и аналитической геометрии. 1) Определители второго и третьего порядков. Решение системы линейных уравнений по формулам Крамера. Системы декартовых координат на прямой, на плоскости и в пространстве. Векторы на плоскости и в пространстве. Линейные операции над векторами и их свойства. Проекция вектора на ось, свойства проекций. Понятие о базисе, разложение вектора по базису. Длина и направляющие косинусы вектора. Операции над векторами, заданными в декартовых координатах. Скалярное, векторное и смешанное произведение, их свойства и вычисление в координатной форме. 2) Основные задачи на плоскости. Уравнение линии на плоскости. Различные виды уравнений прямой. Угол между двумя прямыми, взаимное расположение двух прямых, расстояние от точки до прямой. Кривые второго порядка: окружность, эллипс, гипербола и парабола. Их канонические уравнения и основные свойства.
3) Понятие об уравнении поверхности и уравнения линии и точки в пространстве. Основные уравнения плоскости и прямой в пространстве. Взаимное расположение двух плоскостей, двух прямых, прямой и плоскости. Расстояние от точки до плоскости и до прямой. Введение в анализ. Дифференциальное исчисление. 1) Постоянные и переменные величины. Множества, обозначения и символы теории множеств, числовые множества. Функции и способы ее задания. Простейшие, сложные и элементарные функции. 2) Предел Функции в точке и в бесконечности, односторонние пределы. Бесконечно малые, бесконечно большие и ограниченные функции; их основные свойства. Теоремы о функциях, имеющих предел. Неопределенности различных видов. Первый замечательный предел. Основные понятия о числовой последовательности и ее пределе. Второй замечательный предел. Непрерывность функции в точке и на промежутке. Формулировки основных свойств функций, непрерывных на отрезке. Классификация точек разрыва. 3) Определение производной. Геометрический и механический смысл производной, уравнение касательной к плоскости кривой. Дифференцируемость функции в точке и на множестве. Производная сложной функции. Определение и дифференцирование обратной функции. Производные обратных тригонометрических функций. Формулы и правила дифференцирования элементарных функций. 4) Дифференциал функции, его геометрический смысл и свойства. Параметрическое задание функции; производная функции, заданной параметрическими уравнениями. Производные и дифференциалы высших порядков. Основные теоремы дифференциального исчисления: теорема Ферма, теорема Ролля, теорема Лагранжа, правило Лопиталя. 5) Определение монотонных функций, достаточные признаки монотонности. Точки экстремума, экстремум, необходимые и достаточные условия экстремума. Наибольшее и наименьшее значения функции. Выпуклость, вогнутость, точки перегиба и асимптоты графика функции. Исследование функций и построение их графиков. Функции нескольких переменных. Функции двух и трех переменных, основные понятия и обозначения. Частные приращения и частные производные. Полное приращение и полный дифференциал. Частные производные высших порядков. Экстремум функции двух переменных. Понятие об эмпирических формулах и методе наименьших квадратов.
Интегральное исчисление. 1) Первообразная функция и неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Непосредственное интегрирование, интегрированпие6 заменой переменной, интегрирование по частям. Специальные приемы интегрирования некоторых тригонометрических выражений и функций, содержащих квадратный трехчлен. Интегрирование простейших видов иррациональностей. Понятие о «неберущихся» интегралах и неэлементарных функциях. 2) Определение и основные свойства определенного интеграла. Интеграл с переменным верхним пределом, теорема Барроу. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Несобственные интегралы от непрерывной функции по бесконечному промежутку. Интеграл Пауссона. 3) Задача о вычислении площади криволинейной трапеции. Вычисление площадей плоских фигур, объемов тел вращения и длин дуг плоских кривых. Дифференциальные уравнения. 1) Понятие о дифференциальном уравнении, его порядке и решении. Дифференциальные уравнения первого порядка: понятие решения; постановка задачи Коши, ее геометрический и механический смысл; понятия общего и частного решений. Интегрирование дифференциальных уравнений с разделяющимися переменными и линейных уравнений первого порядка. 2) Дифференциальные уравнения второго порядка: понятие решения; постановка задачи Коши, ее геометрический и механический смысл; понятия общего и частного решений. Общие свойства решений линейных дифференциальных уравнений второго порядка. Понятие о комплексных числах и комплексных функциях действительного аргумента, формула Эйлера. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами со специальной правой частью и их решение методом неопределенных коэффициентов. Ряды. 1) Числовые ряды, основные понятия. Исследование сходимости геометрического и гармонического рядов. Необходимые условия сходимости. Основные свойства сходящихся рядов. Достаточные признаки сходимости рядов с положительными членами: первый признак сравнения, признак Даламбера. Знакочередующиеся и знакопеременные ряды. Признак Лейбница, оценка остатка сходящегося знакочередующегося ряда. Абсолютная и условная сходимость числовых рядов. 2) Понятие о функциональном ряде. Степенной ряд. Теорема Абеля. Интервал и радиус сходимости. Свойства сходящихся степенных рядов. Разложение некоторых элементарных функций в степенной ряд Маклорена. Условия сходимости ряда Маклорена к разлагаемой функции. Применение рядов Маклорена к приближенным вычислениям значений функций и к вычислению определенных интегралов. Теория вероятностей. 1) Определение события. Случайные, достоверные и невозможные события. Основные операции над событиями. Основные свойства операций над событиями. Определение поля событий. Определение совместимых, несовместимых событий. Определение полной группы событий. Понятие вероятности события. Три аксиомы теории вероятностей. Принцип сложения вероятностей несовместимых событий. Условная вероятность одного случайного события относительного другого события. Принцип умножения вероятностей несовместимых событий. Три следствия из аксиом теории вероятностей. Классическое и статистическое определение вероятности случайного события. Элементы комбинаторики. Правило суммы и правило произведения. Размещения, перестановки и сочетания. Формулы для их вычисления. Теорема сложения вероятностей совместимых событий. Зависимые и независимые события. Правило умножения вероятностей независимых событий. Формула полной вероятности. Формула Байеса.
2) Определение дискретной случайной величины. Закон распределения дискретной случайной величины. Способы задания дискретной случайной величины. Геометрический закон распределения дискретной случайной величины. Биномиальное распределение вероятностей дискретной случайной величины. Формула Бернулли. Распределение Пуассона дискретной случайной величины. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа, теорема Пуассона. Определение математического ожидания дискретной случайной величины. Основные свойства математического ожидания. Формула для вычисления. Определение дисперсии дискретной случайной величины. Основные свойства дисперсии. Формула для вычисления. Определение среднего квадратического отклонения. 3) Непрерывные случайные величины. Определение интегральной функции распределения вероятностей непрерывной случайной величины. Основные свойства. Определение дифференциальной функции распределения вероятностей непрерывной случайной величины. Основные свойства. Определение математического ожидания, дисперсии и среднего квадратического отклонения непрерывной случайной величины. Закон равномерного распределения непрерывной случайной величины на отрезке. Показательное распределение непрерывной случайной величины. Нормальный закон распределения вероятностей непрерывной случайной величины. Закон больших чисел. 8. Рекомендуемая литература. 1. Баврин И.И., Матросов В.Л. Общий курс высшей математики. – М.: Просвещение, 1995. – 464 с. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. М.: Высшая школа, 1997. – 400 с. 3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. М.: Высшая школа, 1997. – 479 с.
4. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах: В 2-х ч. Ч. 1. – 4-е изд., испр. и доп. – М.: Высшая школа, 1986. – 304 с.; Ч. II. – 4-е изд., испр. и доп. – М.: Высшая школа, 1986. – 415 с. 5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – 6-е изд. – М.: Наука, 1986. – 576 с. 6. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1977. – 352 с.
Часть 2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Самостоятельная работа над учебным материалом является составной частью обучения студента дневной формы и основной формой обучения студента-заочника. Она складывается из чтения учебника или конспекта лекций, решения задач, самопроверки и выполнения контрольных работ или типовых расчетов. Кроме этого, студент может обращаться с вопросами к преподавателю для получения письменной или устной консультации. Полезно знать и применять на практике следующие основные принципы организации самостоятельной работы по ее отдельным видам. Чтение учебника. 1) Изучая материалы по учебнику или конспекту, следует переходить к следующему вопросу только после правильного понимания предыдущего, проделывая на бумаге все вычисления (в том числе и те, которые по их простоте пропущены в первоисточнике), воспроизводя имеющиеся чертежи. 2) Особое внимание следует обращать на определение основных понятий и формулировку теорем. Следует подробно разбирать примеры, которые поясняют такие определения, и уметь строить аналогичные примеры самостоятельно. Формулировка каждой теоремы состоит из предположений и утверждения. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каждом месте доказательства использовано каждое предположение теоремы. Полезно составлять схемы доказательств сложных теорем. 3) Рекомендуется выписывать определения, формулировки теорем, формулы и уравнения на отдельные листы. На полях их следует отмечать вопросы, выделенные для письменной или устной консультации с преподавателем. Опыт показывает, что такие листы помогают не только запомнить основные положения курса, но и могут служить постоянным индивидуальным справочником для студента. Решение задач. 1) Чтение учебника или конспекта должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь. Полезно до начала вычислений составить краткий плен решения. Решения задач и примеров следует излагать подробно, обосновывать каждый этап решения. Исходя из теоретических положений курса. Вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. В промежуточных вычислениях не следует вводить приближенные значения корней, числа 2) Решение каждого задания должно доводиться до окончательного ответа, которого требует условие. Полученный ответ следует проверить способами, вытекающими из существа данной задачи. Если, например, решалась задача с конкретными физическими или геометрическим содержанием, то полезно прежде всего проверить полученного ответа. Полезно также, если возможно, решить задачу несколькими способами и сравнить полученные результаты.
3) Решение задач определенного типа нужно продолжать до приобретения твердых навыков в их решении. Однако здесь следует предостеречь от весьма распространенной ошибки, заключающейся в том, что благополучное решение задач воспринимается студентом как признак хорошего усвоения теории. Правильное решение задачи часто получается в результате применения механически заученных формул и указаний по их использованию без понимания сущности. Можно сказать, что умение решать задачи является необходимым, но недостаточным условием хорошего знания теории. Самопроверка. 1) После изучения определенной темы по учебнику или конспекту и решения достаточного количества соответствующих задач рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем, проверяя себя каждый раз по первоисточнику. В случае неудовлетворительного результата надо еще раз внимательно разобраться в материале учебника и конспекта, порешать задачи. 2) Иногда недостаточность усвоения того или иного вопроса выясняется только при изучении дальнейшего материала. В этом случае надо вернуться назад и повторить плохо усвоенный раздел. Консультации. 1) Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, разрешить которые самостоятельно не удается (неясность терминов, формулировок теорем, отдельных задач и др.), он может обратиться к преподавателю для получения от него указаний в виде письменной или устной консультации. 2) В своих запросах студент должен точно указывать, в чем он испытывает затруднения. Если он не разобрался в теоретических объяснениях, в доказательстве теоремы или в выводе формулы по учебнику, то нужно указать, какой это учебник, год его издания, страницу, где рассмотрен затрудняющий его вопрос, и что его затрудняет. Если студент испытывает затруднение при решении задачи, то следует указать характер этого затруднения и привести свой предполагаемый план решения. 3) За консультацией следует обращаться и в случаях, если возникают сомнения в правильности ответов для самопроверки или ответов решаемых задач. Контрольные работы. 1) В процессе изучения математики студент должен выполнить ряд контрольных работ. Рецензии преподавателя на эти работы позволяют студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него проблемы, на желательное направление дальнейшей работы; помогают сформулировать вопросы для консультации с преподавателем. 2) Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил эти требования. 3) Распределение контрольных работ по семестрам устанавливается кафедрой в соответствии с распределением по семестрам учебного материала и сообщается студентам дополнительно. Зачеты и экзамены. На экзаменах и зачетах выясняется, прежде всего, отчетливое усвоение всех теоретических и прикладных вопросов программы и умение применять полученные знания к решению практических задач. Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела; решения задач в простейших случаях должны проделываться без ошибок и уверенно. Только при выполнении этих условий знания могут быть признаны удовлетворяющими требованиям, предъявляемым программой. При подготовке к экзамену учебный материал рекомендуется повторять по учебнику и конспекту лекций.
Часть 3. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ При выполнении контрольных работ следует придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены и возвращены студенту для переработки. 1) Каждую контрольную работу следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. 2) На обложке тетради должны быть ясно написаны номер контрольной работы, название дисциплины, фамилия, имя, отчество студента, номер зачетной книжки, номер варианта, специальность и группа, в которой обучается студент. Здесь же указывается домашний адрес и дата отсылки работы в институт. В конце работы следует проставить дату ее выполнения и расписаться. 3) Номер варианта контрольной работы соответствует последней цифре номера зачетной книжки. Если номер зачетной книжки оканчивается цифрой «0», то студент выполняет 10-й вариант. 4) В работу включаются все задачи строго по положенному варианту. Работа, содержащая не все задачи варианта или не своего варианта, не зачитывается. 5) Решения задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач. Перед решением каждой задачи надо выписать полностью ее условие. Решения задач излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи. 6) Если работа не зачтена или сделаны замечания по решению задач, следует выполнить работу над ошибками в той же тетради. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается. 7) Студенты заочного отделения выполняют в течение 3 семестров пять контрольных работ. К экзамену в первом семестре допускаются студенты, у которых зачтены 1-я и 2-я контрольные работы. К зачету во втором семестре допускаются студенты, успешно сдавшие экзамен в первом семестре и имеющие зачтенные 3-ю и 4-ю контрольные работы. К экзамену в третьем семестре допускаются студенты, имеющие зачет за второй семестр и зачтенную 5-ю контрольную работу.
Часть 4. КОНТРОЛЬНЫЕ ЗАДАНИЯ Кривые второго порядка 15. Окружностью радиуса R с центром в точке C (a; b) называется геометрическое место точек плоскости, для которых расстояние до центра С постоянно равно R. 16. Каноническое уравнение окружности с центром в точке 17. Параболой называется геометрическое место точек плоскости, одинаково удаленных от данной точки F, называемой фокусом и от прямой L, называемой директрисой.
19. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек F 1 и F 2, называемых фокусами (| F 1 F 2| = 2 c) есть величина постоянная, равная 2 a > 2 c. 20. Каноническое уравнение эллипса: 21. Гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух данных точек F 1 и F 2, называемых фокусами (| F 1 F 2| = 2 c) есть величина постоянная, равная ± 2 a, где 2 a < 2 c. 22. Каноническое уравнение гиперболы:
Элементы векторной алгебры. 1. Вектором 2. Если 3. Два вектора 4. Сумма векторов 5. Разность векторов 6. Произведение вектора 7. Длина вектора 8. Единичный вектор 9. Скалярное произведение векторов 10. Проекция вектора 11. Угол между векторами 12. Условие ортогональности двух векторов: векторы 13. Условие коллинеарности двух векторов: векторы 14. Направляющие косинусы вектора 15. Векторное произведение векторов 16. Длина векторного произведения
Рис. 5 17. Смешанное произведение векторов 18. Условие компланарности трех векторов: векторы 19. Смешанное произведение трех векторов
Рис. 6 Теория пределов Основные понятия 1. Постоянное число l есть предел функции y = f (х): 2. Если существует 3. Функция a(x) называется бесконечно малой функцией при х → а, если 4. Если a(x) – бесконечно малая функцией при х → а, то Основные теоремы о действиях над функциями, 5. Пусть 1) 2) 3) 4) 5) Если n – натуральное число, то 6) Если n – натуральное число, то 7) Правило замены переменной. Пусть требуется найти предел сложной функции y = f (j(x)) при x → a. Тогда если существует Замечательные пределы 9) Первый замечательный предел: 10) Основные следствия из первого замечательного предела: 1) 3) 5) 7) 9) 11) 13) 15) 11) Второй замечательный предел: 12) Основные следствия из второго замечательного предела: 1) 3) 5) 7) 9) 11) 13) 15) 17) Таблица производных 2. 4. 6. 8. 10. 12. 14. 16. Применение производной 26. Если на некотором промежутке 27. Если функция | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

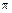 и т.п. Чертежи нужно выполнять аккуратно в соответствии с данными условиями и указанием масштаба.
и т.п. Чертежи нужно выполнять аккуратно в соответствии с данными условиями и указанием масштаба. и радиусом
и радиусом  :
:  (рис. 1).
(рис. 1).




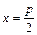

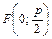

 (рис. 2)
(рис. 2)

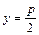
 Рис. 1
Рис. 1
 Рис. 2
Рис. 2
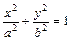 (рис. 3). Точки
(рис. 3). Точки  ,
, 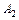 ,
,  и
и  – вершины эллипса; отрезок
– вершины эллипса; отрезок  – большая ось, отрезок
– большая ось, отрезок  – малая ось; параметры
– малая ось; параметры  и
и  – большая и малая полуоси; точки
– большая и малая полуоси; точки 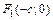 и
и  – левый и правый фокусы; число
– левый и правый фокусы; число 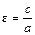 – эксцентриситет;
– эксцентриситет; 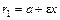 и
и 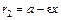 – левый и правый фокальные радиусы. Параметры
– левый и правый фокальные радиусы. Параметры 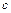 связаны равенством
связаны равенством  .
. (рис. 4). Точки
(рис. 4). Точки  и
и 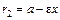 , а для точек правой ветви гиперболы –
, а для точек правой ветви гиперболы –  ; прямые
; прямые 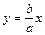 и
и 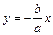 – асимптоты гиперболы. Параметры
– асимптоты гиперболы. Параметры  .
. Рис. 3
Рис. 3
 Рис. 4
Рис. 4
 с началом в точке А и концом в точке В называется направленный отрезок.
с началом в точке А и концом в точке В называется направленный отрезок. и
и  , то координаты вектора равны
, то координаты вектора равны  или
или 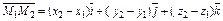 .
. и
и  равны тогда и только тогда, когда
равны тогда и только тогда, когда 
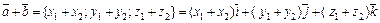 .
. .
. есть вектор
есть вектор  .
. .
. для вектора
для вектора 
 .
. , вычисляемое по формуле:
, вычисляемое по формуле: 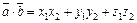 .
. . Аналогично,
. Аналогично,  .
. .
. ) тогда и только тогда, когда
) тогда и только тогда, когда  или
или  .
. ) тогда и только тогда, когда
) тогда и только тогда, когда  или
или  .
. ,
,  и
и  , где a, b, g – углы между вектором
, где a, b, g – углы между вектором  и координатными осями Ox, Oy и Oz соответственно.
и координатными осями Ox, Oy и Oz соответственно.
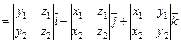 .
.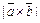 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах 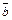 как на сторонах (рис. 5), т. е.
как на сторонах (рис. 5), т. е.  . Площадь треугольника, построенного на этих векторах, равна
. Площадь треугольника, построенного на этих векторах, равна  .
.
 есть число
есть число  .
. .
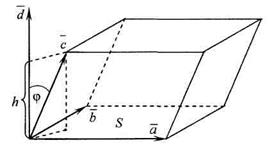
. , взятое по модулю, численно равно объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 6), т. е.
, взятое по модулю, численно равно объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 6), т. е.  . Объем пирамиды, построенной на этих векторах, равен
. Объем пирамиды, построенной на этих векторах, равен 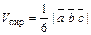 .
.
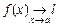 или
или  , если для любого сколь угодно малого числа e > 0 существует число d > 0, зависящее от e такое, что из выполнения неравенства
, если для любого сколь угодно малого числа e > 0 существует число d > 0, зависящее от e такое, что из выполнения неравенства 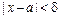 следует неравенство
следует неравенство 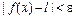 .
. . Аналогично, если существует
. Аналогично, если существует  . Эти пределы называются односторонними пределами.
. Эти пределы называются односторонними пределами. . Аналогично, функция b(х) называется бесконечно большой при х → а, если
. Аналогично, функция b(х) называется бесконечно большой при х → а, если  .
.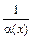 – бесконечно большая функция при х → а; если b(x) – бесконечно большая функцией при х → а, то
– бесконечно большая функция при х → а; если b(x) – бесконечно большая функцией при х → а, то  – бесконечно малая функция при х → а.
– бесконечно малая функция при х → а. ,
, 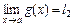 , где l 1, l 2 – конечные, тогда:
, где l 1, l 2 – конечные, тогда: ;
;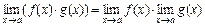 ;
; при
при  ;
; ;
; ;
; ;
; и существует
и существует 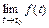 , то справедлива формула
, то справедлива формула 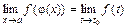 .
. .
. ; 2)
; 2) 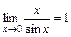 ;
; ; 4)
; 4)  ;
;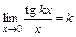 ; 6)
; 6) 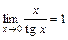 ;
; ; 8)
; 8)  ;
;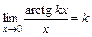 ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14) 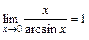 ;
; .
. .
. ; 2)
; 2)  ;
;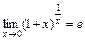 ; 4)
; 4)  ;
; ; 6)
; 6) 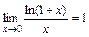 ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14)  ;
;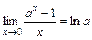 ; 16)
; 16)  ;
; .
. . 3.
. 3. 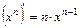 .
. . 5.
. 5.  .
. . 7.
. 7. 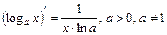 .
. . 9.
. 9.  .
. . 11.
. 11.  .
.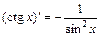 . 13.
. 13.  .
.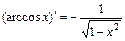 . 15.
. 15.  .
. .
.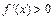 , то на этом промежутке функция
, то на этом промежутке функция  возрастает; если
возрастает; если 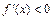 , то функция убывает.
, то функция убывает. непрерывна в точке
непрерывна в точке  и в левой ее окрестности
и в левой ее окрестности 


