
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец решения контрольной работы № 4.Содержание книги
Поиск на нашем сайте Задание 1. Найти общее решение линейного дифференциального уравнения первого порядка Решение. Общее решение будем искать методом Бернулли: Для нахождения частного решения исходного уравнения, удовлетворяющего начальному условию y (0) = 0 подставим в найденное общее решение x = 0 и y = 0 и найдем постоянную С: Ответ: Задание 2. Найти общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида и частное решение, удовлетворяющее начальным условиям y (x 0) = y 0 и 1) 2) 3) Решение. Общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида будем искать в виде 1) Найдем общее решение Найдем частное решение Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y (0) = –1, 2) Найдем общее решение Найдем частное решение Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y (0) = 1, 3) Найдем общее решение Найдем частное решение Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y (0) = 2, Ответ: 1) Задание 3. Написать три первых члена степенного ряда Решение. Запишем три первых члена ряда. При n = 1 получаем первый член ряда: Для данного ряда имеем а = –2, Теперь выясним поведение ряда на концах интервала сходимости. При x = –4 получаем числовой знакочередующийся ряд Ответ: Задание 4. Вычислить определенный интеграл Решение. Для разложения подынтегральной функции в степенной ряд воспользуемся формулой
для любого
Получили числовой знакочередующийся ряд, удовлетворяющий условиям признака Лейбница: 1) члены знакочередующегося ряда убывают по абсолютной величине: Таким образом, Ответ:» 0,042.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 и частное решение, удовлетворяющее начальному условию y (0) = 0.
и частное решение, удовлетворяющее начальному условию y (0) = 0. , где
, где  ,
,  – две новые неизвестные функции, тогда
– две новые неизвестные функции, тогда  . Подставляя в исходное уравнение, получаем
. Подставляя в исходное уравнение, получаем  или
или  . Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получим
. Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получим  Найдем частное решение уравнения (I) при С 1 = 0, которое является ДУ с разделяющимися переменными. Для этого в этом уравнении разделим переменные x и y:
Найдем частное решение уравнения (I) при С 1 = 0, которое является ДУ с разделяющимися переменными. Для этого в этом уравнении разделим переменные x и y: 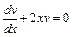 или
или  . Проинтегрировав обе части, получим
. Проинтегрировав обе части, получим 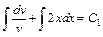 или
или  (при С 1= 0) или
(при С 1= 0) или  – частное решение уравнения (I). Подставляя полученную функцию v в уравнение (II), получаем тоже ДУ с разделяющимися переменными:
– частное решение уравнения (I). Подставляя полученную функцию v в уравнение (II), получаем тоже ДУ с разделяющимися переменными:  , для которого найдем его общее решение. Разделяем переменные:
, для которого найдем его общее решение. Разделяем переменные: 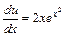 или
или  . Интегрируем обе части:
. Интегрируем обе части: 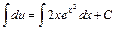 или
или  – общее решение уравнения
– общее решение уравнения 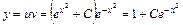 – общее решение исходного уравнения.
– общее решение исходного уравнения. или
или  , т. е. С = –1. Таким образом,
, т. е. С = –1. Таким образом,  – частное решение исходного уравнения при y (0) = 0.
– частное решение исходного уравнения при y (0) = 0.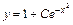 – общее решение;
– общее решение; 
 , y (0) = –1,
, y (0) = –1,  ;
; , y (0) = 1,
, y (0) = 1,  ;
; , y (0) = 2,
, y (0) = 2,  .
. , где
, где  – общее решение соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами, а
– общее решение соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами, а  – некоторое частное решение исходного уравнения.
– некоторое частное решение исходного уравнения.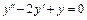 . Характеристическое уравнение
. Характеристическое уравнение  имеет два равных корня
имеет два равных корня 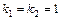 , значит
, значит  .
. есть формула вида
есть формула вида  , причем n = 1 и a = 0 – не корень характеристического уравнения. Поэтому частное решение
, причем n = 1 и a = 0 – не корень характеристического уравнения. Поэтому частное решение  , где А и В – неопределенные коэффициенты. Тогда
, где А и В – неопределенные коэффициенты. Тогда 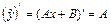 и
и  . Подставив
. Подставив  ,
,  в исходное уравнение, получим –2 А + Ax + B = x – 4 или Ax + (–2 А + B) = x – 4. Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений
в исходное уравнение, получим –2 А + Ax + B = x – 4 или Ax + (–2 А + B) = x – 4. Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений  Отсюда A = 1, B = –2. Поэтому частное решение исходного уравнения имеет вид
Отсюда A = 1, B = –2. Поэтому частное решение исходного уравнения имеет вид 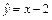 . Следовательно,
. Следовательно,  – общее решение исходного уравнения.
– общее решение исходного уравнения. . Подставим начальные условия в найденное общее решение и его производную, получим систему
. Подставим начальные условия в найденное общее решение и его производную, получим систему  или
или  Отсюда С 1 = С 2 = 1. Таким образом, искомое частное решение имеет вид:
Отсюда С 1 = С 2 = 1. Таким образом, искомое частное решение имеет вид:  .
. . Составим характеристическое уравнение
. Составим характеристическое уравнение  , дискриминант
, дискриминант  , имеет два комплексных корня
, имеет два комплексных корня  ,
,  . Следовательно,
. Следовательно, 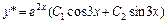 .
. есть формула вида
есть формула вида  , причем n = m = 0, a = 0, b = 3. Так как числа
, причем n = m = 0, a = 0, b = 3. Так как числа  – не корни характеристического уравнения (r = 0), то частное решение имеет вид:
– не корни характеристического уравнения (r = 0), то частное решение имеет вид: 
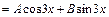 , где А и В – неопределенные коэффициенты,
, где А и В – неопределенные коэффициенты, 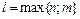 . Найдем
. Найдем  и
и 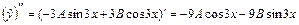 . Подставив
. Подставив 
 или
или 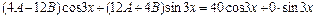 . Приравнивая коэффициенты при синусе и косинусе в обеих частях, получаем систему уравнений
. Приравнивая коэффициенты при синусе и косинусе в обеих частях, получаем систему уравнений  Отсюда A = 1, B = –3. Поэтому частное решение исходного уравнения имеет вид
Отсюда A = 1, B = –3. Поэтому частное решение исходного уравнения имеет вид  . Следовательно,
. Следовательно,  – общее решение исходного уравнения.
– общее решение исходного уравнения.
 . Подставляя начальные условия в найденное общее решение и его производную, получим систему
. Подставляя начальные условия в найденное общее решение и его производную, получим систему  или
или  Следовательно, С 1 = 0, С 2 = 3. Таким образом,
Следовательно, С 1 = 0, С 2 = 3. Таким образом,  – искомое частное решение.
– искомое частное решение. . Характеристическое уравнение
. Характеристическое уравнение  имеет два различных корня
имеет два различных корня  и
и  , значит
, значит  .
. есть формула вида
есть формула вида  , где А – неопределенный коэффициент. Тогда
, где А – неопределенный коэффициент. Тогда 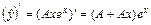 и
и  . Подставим
. Подставим  . Сократив оби части равенства на
. Сократив оби части равенства на  и приведя подобные, получим
и приведя подобные, получим  . Поэтому частное решение исходного уравнения имеет вид
. Поэтому частное решение исходного уравнения имеет вид  . Следовательно,
. Следовательно, 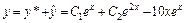 – общее решение исходного уравнения.
– общее решение исходного уравнения. . Подставим начальные условия в найденное общее решение и его производную, получим систему
. Подставим начальные условия в найденное общее решение и его производную, получим систему  или
или  Отсюда С 1 = С 2 = 1. Итак, частное решение исходного уравнения имеет вид
Отсюда С 1 = С 2 = 1. Итак, частное решение исходного уравнения имеет вид  .
. .
. , найти его область абсолютной сходимости.
, найти его область абсолютной сходимости. , при n = 2 – второй член:
, при n = 2 – второй член:  и при n = 3 – третий член ряда:
и при n = 3 – третий член ряда:  .
. ,
,  . Найдем радиус сходимости
. Найдем радиус сходимости  . Тогда интервал абсолютной сходимости ряда по формуле (a – R; a + R) есть (–4; 0).
. Тогда интервал абсолютной сходимости ряда по формуле (a – R; a + R) есть (–4; 0).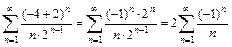 , который сходится согласно признаку Лейбница, т. к. выполняются оба условия признака: 1)
, который сходится согласно признаку Лейбница, т. к. выполняются оба условия признака: 1)  и 2) члены ряда убывают по абсолютной величине
и 2) члены ряда убывают по абсолютной величине  При x = 0 имеем числовой знакоположительный ряд
При x = 0 имеем числовой знакоположительный ряд 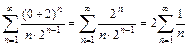 . Это гармонический ряд, который расходится. Таким образом, область абсолютной сходимости исходного ряда имеет вид [–4; 0).
. Это гармонический ряд, который расходится. Таким образом, область абсолютной сходимости исходного ряда имеет вид [–4; 0). с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.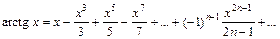 таблицы основных разложений. Заменив в ней x на x 2, получим:
таблицы основных разложений. Заменив в ней x на x 2, получим: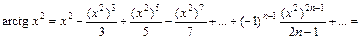

 . Так как отрезок интегрирования [0; 0,5] целиком содержится внутри области сходимости ряда, то на основании свойства о почленном интегрировании степенных рядов получим
. Так как отрезок интегрирования [0; 0,5] целиком содержится внутри области сходимости ряда, то на основании свойства о почленном интегрировании степенных рядов получим

 и 2) предел его общего члена при
и 2) предел его общего члена при 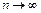 равен нулю:
равен нулю: 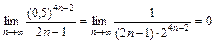 . Так как | a 2| = 0,000372 < 0,001, то приближенное значение суммы S полученного ряда будет равно: S» S 1 = a 1, так как по следствию из признака Лейбница погрешность вычисления r 2 = | S – S 1| < | a 2| < 0,001.
. Так как | a 2| = 0,000372 < 0,001, то приближенное значение суммы S полученного ряда будет равно: S» S 1 = a 1, так как по следствию из признака Лейбница погрешность вычисления r 2 = | S – S 1| < | a 2| < 0,001. .
.


