Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа № 1. «Аналитическая геометрия и векторная алгебра».Содержание книги
Поиск на нашем сайте
1. Даны вершины A (x 1; y 1), B (x 2; y 2), C (x 3; y 3) треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение медианы CM, проведенной из вершины С; 3) уравнение высоты СH, проведенной из вершины С; 4) уравнение прямой L, проходящей через вершину С параллельно стороне АВ; 5) длину высоты СH; 6) величину внутреннего угла А (в радианах). Сделать чертеж. 1. A (1; 1), B (7; 4), C (4; 5). 2. A (1; 1), B (–5; 4), C (–2; 5). 3. A (–1; 1), B (5; 4), C (2; 5). 4. A (–1; 1), B (–7; 4), C (–4; 5). 5. A (1; –1), B (7; 2), C (4; 5). 6. A (1; –1), B (–5; 2), C (–2; 3). 7. A (–1; –1), B (5; 2), C (2; 3). 8. A (–1; –1), B (–7; 2), C (–4; 3). 9. A (0; 1), B (6; 4), C (3; 5). 10. A (1; 0), B (7; 3), C (4; 4). 2. Составить уравнение и построить линию, для каждой точки которой выполняются следующее условие: 1) расстояние ее до точки F (–1; –2) равно расстоянию от прямой x = –3; 2) отношение расстояний до точки F (7; 0) и прямой x = 1 равно 3) отношение расстояний до точки F (2; 0) и прямой x = 3 равно 4) расстояние ее до точки F (3; 3) равно расстоянию от прямой x = –2; 5) отношение расстояний до точки F (2; 0) и прямой 6) отношение расстояний до точки F (–1; 0) и прямой x = –9 равно 7) расстояние ее до точки F (–3; 2) равно расстоянию от прямой x = 2; 8) отношение расстояний до точки F (3; 0) и прямой x = 2 равно 9) отношение расстояний до точки F (–4,5; 0) и прямой x = –8 равно 10) расстояние ее до точки F (1; 0) равно расстоянию от прямой x = 3. 3. Написать разложение вектора 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 4. Даны вершины A 1(x 1; y 1; z 1), A 2(x 2; y 2; z 2), A 3(x 3; y 3; z 3), A 4(x 4; y 4; z 4) пирамиды A 1 A 2 A 3 A 4. Найти: 1) угол между ребрами A 1 A 3 и A 1 A 4; 2) площадь грани A 1 A 2 A 3; 3) уравнение плоскости, содержащей грань A 1 A 2 A 3; 4) уравнение высоты пирамиды, проведенной через вершину A 4. Сделать схематический чертеж. 1. A 1(2; 1; –4), A 2(1; –2; 3), A 3(1; –2; –3), A 4(5; –2; 1). 2. A 1(2; –1; 3), A 2(–5; 1; 1), A 3(0; 3; –4), A 4(–1; –3; 4). 3. A 1(5; 3; 2), A 2(1; –8; 8), A 3(4; –1; 2), A 4(1; 4; –1). 4. A 1(–2; 3; 4), A 2(4; 2; –1), A 3(2; –1; 4), A 4(–1; –1; 1). 5. A 1(4; –4; 0), A 2(–5; 3; 2), A 3(8; 0; 1), A 4(2; 2; 3). 6. A 1(–3; –4; 0), A 2(0; –1; 3), A 3(–6; 4; 2), A 4(–3; 0; 3). 7. A 1(0; 4; –4), A 2(5; 1; –1), A 3(–1; –1; 3), A 4(0; –3; 7). 8. A 1(0; –6; 3), A 2(3; 3; –3), A 3(–3; –5; 2), A 4(–1; –4; 0). 9. A 1(2; –1; –3), A 2(0; 0; 0), A 3(5; –1; –1), A 4(–1; –1; 1). 10. A 1(1; 5; 8), A 2(–2; 1; 4), A 3(3; –2; –3), A 4(1; –1; 0). Основные теоретические сведения. Аналитическая геометрия на плоскости. Простейшие задачи на плоскости 1. Расстояние между двумя точками
2. Если 3. Если Различные виды уравнения прямой на плоскости 4. Уравнение прямой, проходящей через данную точку 5. Уравнение прямой с угловым коэффициентом: 6. Уравнение прямой, проходящей через две данные точки 7. Уравнение прямой в отрезках на осях: 8. Нормальное уравнение прямой: 9. Общее уравнение прямой: 10. Чтобы общее уравнение прямой Расстояние от точки до прямой 11. Расстояние от точки Взаимное расположение двух прямых на плоскости 12. Угол между прямыми 13. Условие параллельности двух прямых: прямые 14. Условие перпендикулярности двух прямых: прямые Кривые второго порядка 15. Окружностью радиуса R с центром в точке C (a; b) называется геометрическое место точек плоскости, для которых расстояние до центра С постоянно равно R. 16. Каноническое уравнение окружности с центром в точке 17. Параболой называется геометрическое место точек плоскости, одинаково удаленных от данной точки F, называемой фокусом и от прямой L, называемой директрисой.
19. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек F 1 и F 2, называемых фокусами (| F 1 F 2| = 2 c) есть величина постоянная, равная 2 a > 2 c.
20. Каноническое уравнение эллипса: 21. Гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух данных точек F 1 и F 2, называемых фокусами (| F 1 F 2| = 2 c) есть величина постоянная, равная ± 2 a, где 2 a < 2 c. 22. Каноническое уравнение гиперболы:
Элементы векторной алгебры. 1. Вектором 2. Если 3. Два вектора 4. Сумма векторов 5. Разность векторов 6. Произведение вектора 7. Длина вектора 8. Единичный вектор 9. Скалярное произведение векторов 10. Проекция вектора 11. Угол между векторами 12. Условие ортогональности двух векторов: векторы 13. Условие коллинеарности двух векторов: векторы 14. Направляющие косинусы вектора 15. Векторное произведение векторов 16. Длина векторного произведения
Рис. 5 17. Смешанное произведение векторов 18. Условие компланарности трех векторов: векторы 19. Смешанное произведение трех векторов
Рис. 6
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.205.148 (0.009 с.) |

 ;
; ;
; равно
равно  ;
; ;
; ;
; ;
; по векторам
по векторам  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
, 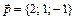 ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. и
и  вычисляется по формуле:
вычисляется по формуле:  .
. , делящей направленный отрезок
, делящей направленный отрезок  в отношении
в отношении  , вычисляются по формулам:
, вычисляются по формулам:  ,
,  . В частности, если точка
. В частности, если точка  пополам (
пополам ( ), то
), то  ,
,  .
. – вершины D
– вершины D  , то его площадь вычисляется по формуле:
, то его площадь вычисляется по формуле:  .
. в данном направлении
в данном направлении  :
:  .
. .
. . Угловой коэффициент для такой прямой
. Угловой коэффициент для такой прямой  .
. , где параметры a и b равны величинам отрезков, которые прямая отсекает от оси Ox и Oy соответственно.
, где параметры a и b равны величинам отрезков, которые прямая отсекает от оси Ox и Oy соответственно. , где параметр p > 0 равен длине нормали, проведенной к прямой из начала координат, a – угол между нормалью и положительной частью оси Ox.
, где параметр p > 0 равен длине нормали, проведенной к прямой из начала координат, a – угол между нормалью и положительной частью оси Ox. , где A и B одновременно не равны нулю.
, где A и B одновременно не равны нулю. . Знак перед корнем выбирается противоположным знаку коэффициента
. Знак перед корнем выбирается противоположным знаку коэффициента  .
. до прямой
до прямой  .
. и
и  вычисляется по формуле:
вычисляется по формуле:  .
. .
. .
. и радиусом
и радиусом  :
:  (рис. 1).
(рис. 1).




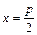

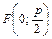

 (рис. 2)
(рис. 2)

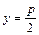
 Рис. 1
Рис. 1
 Рис. 2
Рис. 2
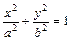 (рис. 3). Точки
(рис. 3). Точки  ,
, 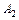 ,
,  и
и  – вершины эллипса; отрезок
– вершины эллипса; отрезок  – большая ось, отрезок
– большая ось, отрезок  – малая ось; параметры
– малая ось; параметры  и
и  – большая и малая полуоси; точки
– большая и малая полуоси; точки 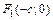 и
и  – левый и правый фокусы; число
– левый и правый фокусы; число 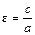 – эксцентриситет;
– эксцентриситет; 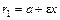 и
и 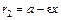 – левый и правый фокальные радиусы. Параметры
– левый и правый фокальные радиусы. Параметры 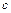 связаны равенством
связаны равенством  .
. (рис. 4). Точки
(рис. 4). Точки  и
и 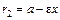 , а для точек правой ветви гиперболы –
, а для точек правой ветви гиперболы –  ; прямые
; прямые 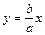 и
и 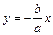 – асимптоты гиперболы. Параметры
– асимптоты гиперболы. Параметры  .
. Рис. 3
Рис. 3
 Рис. 4
Рис. 4
 с началом в точке А и концом в точке В называется направленный отрезок.
с началом в точке А и концом в точке В называется направленный отрезок. и
и  , то координаты вектора равны
, то координаты вектора равны  или
или 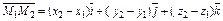 .
. и
и  равны тогда и только тогда, когда
равны тогда и только тогда, когда 
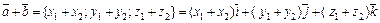 .
. .
. есть вектор
есть вектор  .
. .
. для вектора
для вектора 
 .
. , вычисляемое по формуле:
, вычисляемое по формуле: 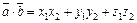 .
. . Аналогично,
. Аналогично,  .
. .
. ) тогда и только тогда, когда
) тогда и только тогда, когда  или
или  .
. ) тогда и только тогда, когда
) тогда и только тогда, когда  или
или  .
. ,
,  и
и  , где a, b, g – углы между вектором
, где a, b, g – углы между вектором  и координатными осями Ox, Oy и Oz соответственно.
и координатными осями Ox, Oy и Oz соответственно.
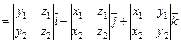 .
.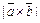 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах 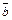 как на сторонах (рис. 5), т. е.
как на сторонах (рис. 5), т. е.  . Площадь треугольника, построенного на этих векторах, равна
. Площадь треугольника, построенного на этих векторах, равна  .
.
 есть число
есть число  .
. .
. , взятое по модулю, численно равно объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 6), т. е.
, взятое по модулю, численно равно объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 6), т. е.  . Объем пирамиды, построенной на этих векторах, равен
. Объем пирамиды, построенной на этих векторах, равен 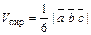 .
.