
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец решения контрольной работы № 1.Содержание книги
Поиск на нашем сайте
Задание 1. Даны вершины А (–1; 0), В (5; 2), С (2; 4) треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение медианы CM, проведенной из вершины С; 3) уравнение высоты СH, проведенной из вершины С; 4) уравнение прямой L, проходящей через вершину С параллельно стороне АВ; 5) длину высоты СH; 6) величину внутреннего угла А. Сделать чертеж.
1) Длину стороны АВ найдем, используя формулу расстояния между двумя точками на плоскости: Подставляя в нее координаты точек А (–1; 0) и В (5; 2), получим: 2) По определению медианы точка М медианы CМ делит сторону АВ пополам. Следовательно, ее координаты определяются по формулам деления отрезка пополам:
Таким образом, найдена точка М (2; 1). Уравнение медианы CМ найдем как уравнение прямой, проходящей через две заданные точки C и М, по формуле: По свойству пропорции отсюда следует уравнение CМ:
3) Уравнение высоты СH как прямой, проходящей через точку С перпендикулярно стороне АВ, будем искать в виде Угловой коэффициент Уравнение высоты примет теперь вид: 4) Аналогично, уравнение прямой L, проходящей через вершину С параллельно стороне АВ, будем искать в виде: Уравнение прямой L примет вид: 5) Длину высоты СН найдем, используя формулу расстояния от точки С до прямой АВ: Найдем уравнение стороны АВ: Подставляя в найденное уравнение координаты точки С, получим: 6) Из рисунка видно, что внутренний угол А треугольника АВС есть угол, на который нужно повернуть сторону АВ в положительном направлении (т. е. против часовой стрелки) до совмещения ее со стороной АС. Поэтому тангенс угла А найдем по формуле: Угловой коэффициент Ответ: 1) длина стороны АВ: Задание 2. Составить уравнение и построить линию, для каждой точки которой выполняется следующее условие: отношение расстояний до точки F (–1; 0) и прямой Решение. Сделаем схематический чертеж по условию задачи.
1) Предположим, что М (x; y) – текущая точка искомой линии. Тогда точка N (–4; y) является ее проекцией на прямой x = –4. 2) По условию задачи выполняется следующее отношение расстояний: 3) Используя формулу расстояния между двумя точками, выразим полученное буквенное равенство в координатной форме и преобразуем его к виду канонического уравнения одной из кривых второго порядка (окружности, эллипса, гиперболы или параболы):
 или или  , или , или 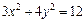 . .
Получили каноническое уравнение эллипса: 4) Построим линию по ее уравнению.
Ответ: Задание 3. Написать разложение вектора Решение. Требуется представить вектор
Т. к.
Т. о., по формулам Крамера: Ответ: Задание 4. Даны вершины A 1(1; –1; 2), A 2(2; 1; 2), A 3(1; 1; 4),
1) Найдем векторы
Находим косинус угла между векторами по формуле:
2) Гранью A 1 A 2 A 3 пирамиды A 1 A 2 A 3 A 4 является треугольник A 1 A 2 A 3, площадь которого определим по формуле: Координаты вектора Вычислим теперь векторное произведение векторов
Тогда длина векторного произведения равна:
Т. о., получим: 3) Уравнение искомой плоскости составим как уравнение плоскости, проходящей через три данные точки A 1, A 2, A 3 в форме определителя 3-го порядка:
4) Уравнение высоты, опущенной из точки А 4 на грань А 1 А 2 А 3 найдем как прямую, проходящую через точку А 4 перпендикулярно плоскости А 1 А 2 А 3 в форме канонических уравнений прямой Ответ: 1) величина угла между ребрами A 1 A 3 и A 1 A 4:
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.34.148 (0.009 с.) |

 Решение. Изобразим заданный треугольник в декартовой системе координат Oxy.
Решение. Изобразим заданный треугольник в декартовой системе координат Oxy.
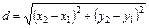 .
. (ед.).
(ед.). ,
,  .
. или
или  , или
, или 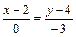 .
. или
или  .
.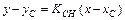 , где угловой коэффициент
, где угловой коэффициент  найдем из условия перпендикулярности прямых СH и АВ:
найдем из условия перпендикулярности прямых СH и АВ:  .
. определим, используя формулу углового коэффициента прямой:
определим, используя формулу углового коэффициента прямой:  . Следовательно,
. Следовательно,  .
. или
или  .
.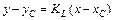 , где угловой коэффициент
, где угловой коэффициент  прямой L найдем из условия параллельности прямых L и AB:
прямой L найдем из условия параллельности прямых L и AB: 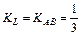 .
. или
или  .
. , где
, где  есть общее уравнение стороны АВ.
есть общее уравнение стороны АВ. или
или  , или
, или  .
. (ед.).
(ед.). .
. (найден в п. 3). Аналогично найдем
(найден в п. 3). Аналогично найдем  . Следовательно,
. Следовательно,  , тогда
, тогда  (рад.).
(рад.). ед.; 2) уравнение медианы CМ:
ед.; 2) уравнение медианы CМ:  ; 3) уравнение высоты СН:
; 3) уравнение высоты СН:  ; 5) длина высоты СН:
; 5) длина высоты СН:  ед.; 6) величина внутреннего угла А:
ед.; 6) величина внутреннего угла А: 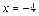 равно
равно  .
.

 или
или  .
.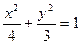
 , у которого полуоси есть
, у которого полуоси есть  и
и  .
.

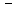 эллипс.
эллипс.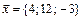 по векторам
по векторам 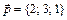 ,
,  ,
, 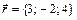 .
. в виде
в виде  , где a, b и g – неизвестные числа. Согласно определения произведения вектора на число и суммы векторов имеем:
, где a, b и g – неизвестные числа. Согласно определения произведения вектора на число и суммы векторов имеем:  ,
,  ,
, 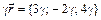 и
и  . Применяя определение равенства двух векторов получим линейную систему трех уравнений относительно неизвестных a, b, g:
. Применяя определение равенства двух векторов получим линейную систему трех уравнений относительно неизвестных a, b, g: 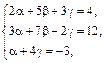 которую решим по формулам Крамера. Для этого составим четыре определителя 3-го порядка и вычислим их по правилу треугольников:
которую решим по формулам Крамера. Для этого составим четыре определителя 3-го порядка и вычислим их по правилу треугольников: .
. , то система имеет единственное решение.
, то система имеет единственное решение.
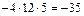 .
.
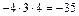 .
.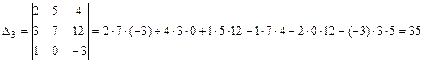 .
. ,
, 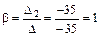 ,
, 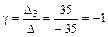 .
. .
. Решение. Сделаем схематический чертеж.
Решение. Сделаем схематический чертеж. и
и  , проходящие через 2 заданные точки:
, проходящие через 2 заданные точки: ,
, .
.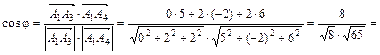
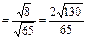 . Следовательно,
. Следовательно,  (рад.).
(рад.). .
. (см. п. 1). Аналогично найдем координаты вектора
(см. п. 1). Аналогично найдем координаты вектора 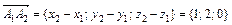 .
. и
и 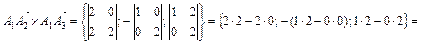
 .
. .
. (кв. ед.).
(кв. ед.). или
или  , или
, или  , или
, или 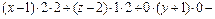
 , или
, или  , или
, или  .
. , где вектор
, где вектор  является направляющем вектором прямой (коллинеарен прямой). В п. 3 было найдено уравнение плоскости А 1 А 2 А 3:
является направляющем вектором прямой (коллинеарен прямой). В п. 3 было найдено уравнение плоскости А 1 А 2 А 3:  . Т. к. вектор
. Т. к. вектор  коллинеарен высоте, то его можно выбрать в качестве направляющего вектора
коллинеарен высоте, то его можно выбрать в качестве направляющего вектора  .
. кв. ед.; 3) уравнение плоскости A 1 A 2 A 3:
кв. ед.; 3) уравнение плоскости A 1 A 2 A 3: 


