
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец решения контрольной работы № 3.Содержание книги
Поиск на нашем сайте
Задание 1. Найти неопределенные интегралы. Результаты проверить дифференцированием. 1) 3) Решение. 1) Интеграл преобразуем к табличному методом замены переменной. Так как
Проверка. Покажем, что производная от найденного неопределённого интеграла равна подынтегральной функции. По свойству неопределённого интеграла это означает, что интеграл найден верно.
2) Преобразуем интеграл к виду
Проверка.
3) Для интегрирования произведения степенной функции на трансцендентную функцию (тригонометрическую, обратно тригонометрическую, показательную или логарифмическую) применяется метод интегрирования по частям, опирающийся на использование формулу интегрирования по частям Пусть Применяя формулу (*), находим:
Проверка.
4) Для нахождения неопределённого интеграла от неправильной рациональной дроби, степень числителя которой больше или равна степени знаменателя, выделим из дроби целый многочлен и правильную дробь, используя деление многочленов «уголком»:
Таким образом, имеем: Следовательно, по свойству неопределённого интеграла
В последнем интеграле квадратный трёхчлен
После этого правильная рациональная дробь
Приводя к общему знаменателю сумму
Из равенства (**) следует, что Подставим найденные значения А и В в равенство (**), получим: Следовательно,
Исходный интеграл в формуле (*) примет вид:
Проверка.
Ответ: 1) Задание 2. Вычислить по формуле Ньютона-Лейбница определенный интеграл Решение. Формула Ньютона – Лейбница имеет вид:
Для вычисления заданного интеграла используем метод замены переменной в определённом интеграле: Найдём пределы интегрирования для новой переменной t. Если
Ответ: Задание 3. Вычислить площадь фигуры, ограниченной графиками функций Решение. Для выполнения чертежа (рисунка фигуры) найдём координаты вершины параболы и точек пересечения параболы с прямой. Вершина параболы находится в точке
По уравнению параболы находим Для нахождения точек пересечения параболы и прямой необходимо решить систему двух уравнений:
Точками пересечения являются
Для вычисления площади S полученной фигуры будем использовать формулу: Вычисляем площадь фигуры:
Ответ: 4,5 (кв. ед.). Задание 4. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной графиками функций Решение. Для выполнения чертежа фигуры найдём координаты точек пересечения параболы с прямой, решив систему двух уравнений:
Точками пересечения являются
Для вычисления объема V, получаемого при вращении данной фигуры вокруг оси Ох, будем использовать формулу: Вычисляем объем:
Ответ:
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.128.229 (0.009 с.) |

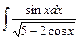 ; 2)
; 2)  ;
;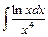 ; 4)
; 4)  .
. , то, вводя новую переменную
, то, вводя новую переменную  находим интеграл:
находим интеграл: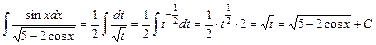 .
.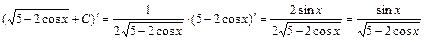 . Интеграл найден верно.
. Интеграл найден верно. :
: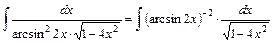 . Учитывая, что
. Учитывая, что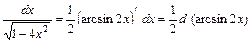 , то после введения новой переменной
, то после введения новой переменной 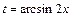 получаем табличный интеграл:
получаем табличный интеграл:
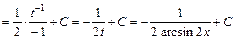 .
.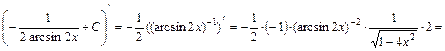
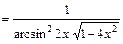 . Интеграл найден верно.
. Интеграл найден верно.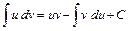 . (*)
. (*)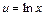 и
и 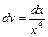 , тогда
, тогда  и
и  .
.
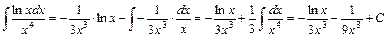 .
.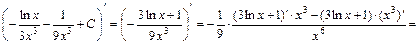
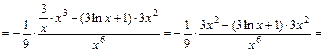
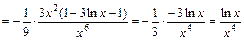 . Интеграл найден верно.
. Интеграл найден верно.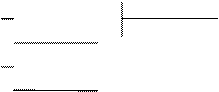
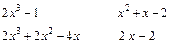
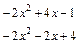
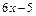

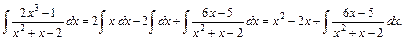 (*)
(*)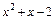 имеет два действительных корня, которые находим из квадратного уравнения
имеет два действительных корня, которые находим из квадратного уравнения  :
: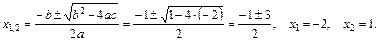
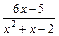 может быть разложена на сумму двух простейших элементарных дробей методом неопределённых (буквенных) коэффициентов следующим образом:
может быть разложена на сумму двух простейших элементарных дробей методом неопределённых (буквенных) коэффициентов следующим образом: (**), где А и В – неопределённые коэффициенты.
(**), где А и В – неопределённые коэффициенты.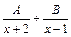 и группируя по степеням переменной х, получаем:
и группируя по степеням переменной х, получаем: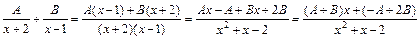 .
.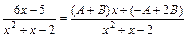 , а это возможно тогда и только тогда, когда
, а это возможно тогда и только тогда, когда  или
или 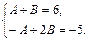 Решая систему двух линейных уравнений с двумя неизвестными, находим неопределенные коэффициенты:
Решая систему двух линейных уравнений с двумя неизвестными, находим неопределенные коэффициенты: 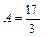 ,
,  .
.
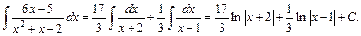
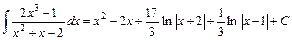 .
.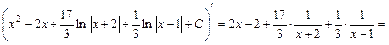
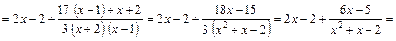
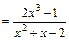 . Интеграл найден верно.
. Интеграл найден верно. ; 2)
; 2) 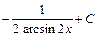 ; 3)
; 3) 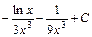 ; 4)
; 4) 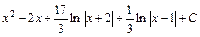 .
.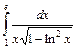 .
.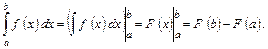
 ,
, 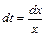 ,
, 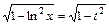 .
. , то
, то 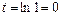 . Если
. Если 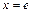 , то
, то 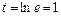 . Итак,
. Итак, 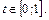 Вычисляем интеграл, переходя к новой переменной с новыми пределами интегрирования:
Вычисляем интеграл, переходя к новой переменной с новыми пределами интегрирования: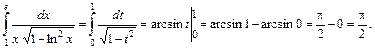
 .
. и
и 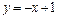 . Сделать чертеж.
. Сделать чертеж.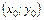 экстремума функции
экстремума функции 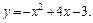 Поэтому найдём производную и приравняем её нулю.
Поэтому найдём производную и приравняем её нулю.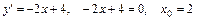
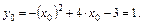 Вершина параболы находится в точке
Вершина параболы находится в точке  , ветви параболы направлены вниз.
, ветви параболы направлены вниз.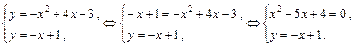
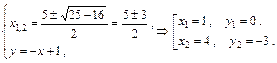
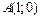 и
и 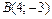 Делаем чертёж фигуры.
Делаем чертёж фигуры.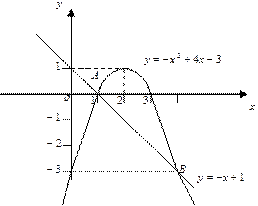
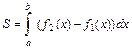 , где
, где 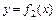 – уравнение кривой, которая ограничивает фигуру сверху, а
– уравнение кривой, которая ограничивает фигуру сверху, а 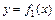 – уравнение кривой, ограничивающей фигуру снизу,
– уравнение кривой, ограничивающей фигуру снизу, 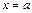 и
и 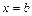 – абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае:
– абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае: 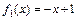 ,
, 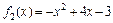 ,
, 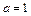 и
и  .
.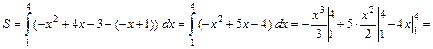
 (кв. ед.).
(кв. ед.). 
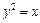 и
и 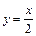 .
.

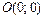 и
и 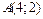 . Делаем чертёж фигуры.
. Делаем чертёж фигуры.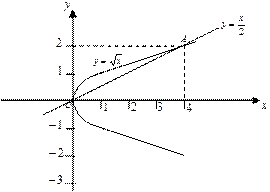
 , где
, где 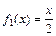 ,
,  ,
, 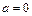 и
и 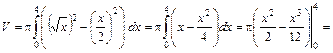
 (куб. ед.).
(куб. ед.). 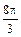 (куб. ед.).
(куб. ед.).


