
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец решения контрольной работы № 2.Содержание книги
Поиск на нашем сайте
Задание 1. Найти пределы функций. 1) 2) Решение. 1) Данный предел в зависимости от значений а) б)
в) Получим:
2) Найдем значения функций
По теореме о пределе корня
3)
Ответ: 1), а) Задание 2. Найти производные заданных функций. 1) 3) Решение. 1) Используем правило дифференцирование суммы
2) Используем правило дифференцирование суммы
где
3) Используем правило дифференцирования суммы
где
Ответ: 1) Задание 3. Провести полное исследование функции Решение. 1) Найдем область определения, интервалы непрерывности и точки разрыва функции. Функция определена на всей числовой оси, кроме точки 2) Выясним четность, нечетность и периодичность функции.
Функция непериодична, т. к. 3) Найдем асимптоты графика функции (вертикальные, горизонтальные и наклонные).
Так как точка
Так как это значение отрицательно, и функция слева от точки Теперь возьмем справа от точки
Так как это значение положительно, и функция справа от точки Таким образом, слева от точки
б) Горизонтальные асимптоты. Для нахождения горизонтальной асимптоты нужно найти предел функции при
Предел равен бесконечности, значит горизонтальной асимптоты нет. в) Наклонные асимптоты. Наклонная асимптота имеет уравнение прямой линии с угловым коэффициентом вида Найдем оба указанных предела для заданной функции:
Таким образом, график имеет наклонную асимптоту 4) Найдем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Находим сначала первую производную функции:
Так как точка Критические точки и точка разрыва Таблица 1.
5) Найдем интервалы выпуклости и вогнутости графика функции, точки перегиба. Находим сначала вторую производную функции:
Так как точка Точка разрыва разбивают числовую ось Ox на 2 интервала, в которых по знаку второй производной Таблица 2.
6) Находим точки пересечения графика функции с осями координат, решая две системы уравнений. С осью Ox:
С осью Oy:
7) Используя результаты исследования, строим график функции в такой последовательности: а) рисуем вертикальную асимптоту
Задание 4. Доказать, что функция Решение. По определению частной производной находим
Аналогично находим частную производную
Находим смешанную частную производную 2-го порядка, используя правило дифференцирования произведения двух функций:
Подставляем найденные частные производные в данное уравнение:
Ответ: что и требовалось доказать.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.141.106 (0.011 с.) |


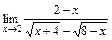 ; 3)
; 3)  .
. вычисляется разными способами.
вычисляется разными способами.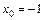 . Найдем значения функций, стоящих в числителе и в знаменателе дроби,
. Найдем значения функций, стоящих в числителе и в знаменателе дроби, 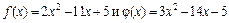 в точке
в точке 
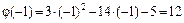 . Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке:
. Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке:  ;
; . Найдем новые значения
. Найдем новые значения 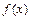 и
и  в точке
в точке 
 . Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке
. Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке  и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель
и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель  , создающий неопределенность вида
, создающий неопределенность вида 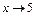 . С этой целью найдем корни уравнений
. С этой целью найдем корни уравнений 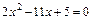 и
и  , затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель
, затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель 
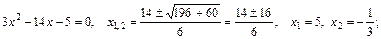
 ;
; . При
. При  имеем
имеем 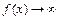 и
и  , т. е. заданное отношение при
, т. е. заданное отношение при  и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной
и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной  . В данном случае это есть
. В данном случае это есть  . После сокращения дроби на критический множитель
. После сокращения дроби на критический множитель  ,
,  ,
,  .
.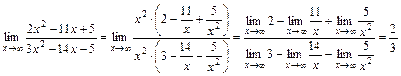 .
. и
и  , стоящих в числителе и знаменателе дроби, в точке
, стоящих в числителе и знаменателе дроби, в точке 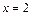 :
:  ,
,  . Следовательно, заданное отношение
. Следовательно, заданное отношение  при
при  является неопределенностью вида
является неопределенностью вида  , создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю
, создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю  и используем формулу сокращенного умножения разности квадратов:
и используем формулу сокращенного умножения разности квадратов:  :
:


 .
.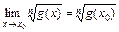 , получим:
, получим: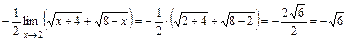 .
. . Найдем значения функций
. Найдем значения функций  и
и  в точке
в точке 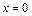 :
: 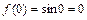 и
и  . Следовательно, заданное отношение представляет собой при
. Следовательно, заданное отношение представляет собой при  неопределенность вида
неопределенность вида  и равенство
и равенство  , вытекающее из непрерывности в точке
, вытекающее из непрерывности в точке  . С этой целью преобразуем заданный предел следующим образом:
. С этой целью преобразуем заданный предел следующим образом:
 .
.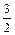 ; б)
; б)  ; в)
; в)  . 2)
. 2)  . 3) 3.
. 3) 3. ; 2)
; 2) 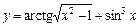 ;
; .
. и правила дифференцирования сложной функции вида
и правила дифференцирования сложной функции вида  , где
, где  , а также таблицу производных. Получим:
, а также таблицу производных. Получим:

 .
. .
. ,
, , а также таблицу производных. Получим:
, а также таблицу производных. Получим:
 .
. и правила дифференцирования сложных функций вида
и правила дифференцирования сложных функций вида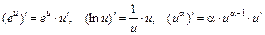 ,
,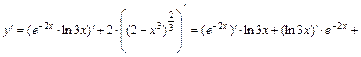

 .
. ; 2)
; 2) 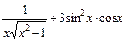 ; 3)
; 3)  .
. и построить ее график.
и построить ее график. , т. е.
, т. е. 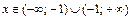 . В каждой точке области определения функция непрерывна. Точка
. В каждой точке области определения функция непрерывна. Точка  , т. е.
, т. е.  . Следовательно, функция не является ни четной, ни нечетной.
. Следовательно, функция не является ни четной, ни нечетной. , где Т – некоторое действительное число.
, где Т – некоторое действительное число.
 и вычислим в нем значение функции и ее знак:
и вычислим в нем значение функции и ее знак: .
. .
. :
: .
. .
.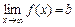 , то прямая, определяемая уравнением
, то прямая, определяемая уравнением  , есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:
, есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел: .
. , где
, где  ,
, 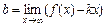 . Если
. Если  , то наклонной асимптоты не существует.
, то наклонной асимптоты не существует.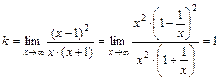 ,
, .
. .
.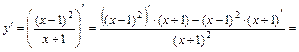
 .
. не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых
не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых 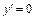 или
или  , т. е.
, т. е. 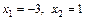 .
.
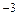





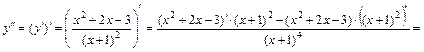

 .
. , то критических точек второго рода нет.
, то критических точек второго рода нет. определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.
определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.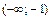

 А (1; 0) – точка пересечения графика с осью Ox.
А (1; 0) – точка пересечения графика с осью Ox. В (0; 1) – точка пересечения графика с осью Oу.
В (0; 1) – точка пересечения графика с осью Oу. и минимум в точке
и минимум в точке  ; в) наносим на осях точки А (1; 0) и В (0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот.
; в) наносим на осях точки А (1; 0) и В (0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот.

 удовлетворяет уравнению
удовлетворяет уравнению 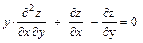 .
. , считая переменную y фиксированной постоянной величиной:
, считая переменную y фиксированной постоянной величиной: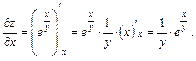
 считая переменную x фиксированной постоянной величиной:
считая переменную x фиксированной постоянной величиной:
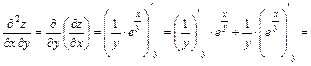
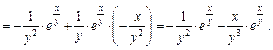
 .
.


