
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение основных элементарных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В ряд Маклорена 1. Запишем разложение в ряд Маклорена функции Так как
Таким образом, получаем следующее разложение:
Поскольку
то есть ряд сходится при любых Аналогично можно получить разложения других функций в ряды Маклорена. 2.
3.
4. 5.
6. Разложение функций в ряды Тейлора и Маклорена используется, например, при вычислении приближенных значений функций, определенных интегралов, решении дифференциальных уравнений и др. Пример 10.14. Функцию Решение. Воспользуемся формулой
в которой заменим Получим следующее разложение в ряд Маклорена
Пример 10.15. Вычислить Решение. Воспользуемся разложением
Так как
Так как четвертый член ряда
Ряды Фурье для периодических функций В электротехнике широкое применение нашли функциональные ряды Фурье. Пусть периодическая функция f (x) с периодом T = 2 l интегрируема на отрезке [– l; l ]. Рядом Фурье функции f (x) с периодом T = 2 l называется функциональный ряд
коэффициенты которого находятся по формулам
В частности, если T = 2 π, то ряд Фурье функции f (x) имеет вид
Теорема о разложимости периодической функции в ряд Фурье. Если периодическая функция f (x) с периодом T=2 l на отрезке [– l; l ] 1) кусочно-монотонна, 2) имеет конечное число точек разрыва 1-го рода, то ряд Фурье функции f (x) сходится для всех действительных х. При этом сумма ряда S (x) = f (x) в точках ее непрерывности и Пример 10.16. Разложить периодическую с периодом T = 2 π функцию Построить графики функции f (x)и суммы ряда S (x). Решение. Найдем коэффициенты ряда Фурье по формулам (10.8):
Аналогично находим коэффициенты bn:
Подставив найденные значения a 0, an, bn в формулу (10.7), запишем разложение функции f (x) в ряд Фурье:
Поскольку
Графики функции f (x) и суммы ряда S (x) изображены на рис.10.1 и рис. 10.2.
Заметим, что в точках разрыва 0, ± π, ±2 π,… функция S (x) принимает значения, равные полусумме значений функции f (x) слева и справа от этих точек.
Если функция f (x) – четная на интервале (– l; l), т. е. f (– x) = f (x), то в формуле (10.5) коэффициенты bn = 0 и ряд Фурье имеет вид:
где Если функция f (x) – нечетная на интервале (– l; l), то есть f (–x) = – f (x), то в формуле (10.5) коэффициенты a 0 = 0, an = 0 и ряд Фурье имеет вид
где Пример 10.17. Разложить в ряд Фурье периодическую с периодом T = 4 функцию Решение. Поскольку функция
При вычислении последнего интеграла воспользуемся формулой интегрирования по частям
Тогда du v Следовательно,
Разложение в ряд Фурье имеет вид
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Исследовать сходимость ряда. 1. 5. Выяснить, сходится ли данный ряд абсолютно, условно или расходится. 8. Найти область сходимости данного ряда. 10. Разложить данную функцию в ряд Маклорена и указать область сходимости полученного ряда. 12. 14. Найти три первых, отличных от нуля члена разложения в сте-пенной ряд решения 15. Разложить в ряд Фурье периодическую с периодом T =4 функцию
КОНТРОЛЬНЫЙ ТЕСТ ПО МОДУЛЮ №10
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.78.108 (0.012 с.) |

 .
.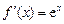 ,
, 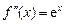 ,…,
,…, 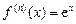 , то
, то
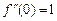 , …,
, …, 

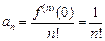 , радиус сходимости данного ряда:
, радиус сходимости данного ряда: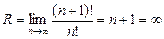 ,
,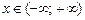 .
.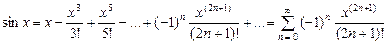 ,
,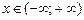 .
.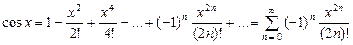 ,
, ,
, 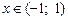 .
.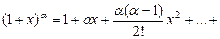
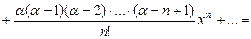
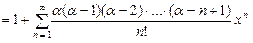 ,
, 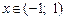 .
.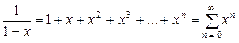 ,
,  разложить в ряд Маклорена.
разложить в ряд Маклорена.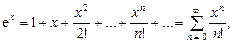
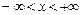 ,
, на
на 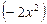 .
.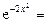
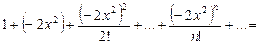
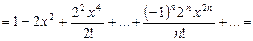
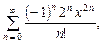
 с точностью
с точностью 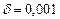 .
. ,
, 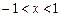 (10.5)
(10.5)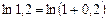 , и
, и  , то полагая в формуле (10.5)
, то полагая в формуле (10.5) 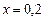 находим
находим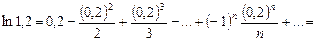
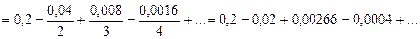
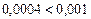 , ограничимся первыми слагаемыми. Значит,
, ограничимся первыми слагаемыми. Значит, .
.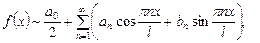 (10.5)
(10.5) ,
,  ,
, 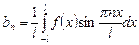 . (10.6)
. (10.6)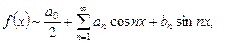 где (10.7)
где (10.7)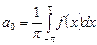 ,
, 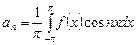 ,
, 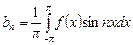 . (10.8)
. (10.8)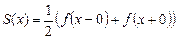 в точках разрыва.
в точках разрыва.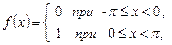 в ряд Фурье.
в ряд Фурье.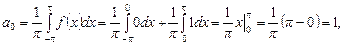

 .
.

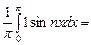
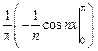
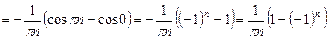 .
.
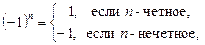 то придавая индексу n последовательно значения n =1,2,3,…,10, запишем сумму первых пяти ненулвых слагаемых ряда (сумму первых гармоник ряда):
то придавая индексу n последовательно значения n =1,2,3,…,10, запишем сумму первых пяти ненулвых слагаемых ряда (сумму первых гармоник ряда):
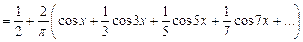 .
.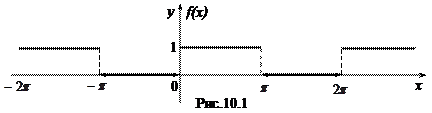

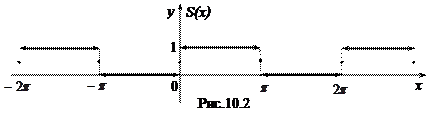
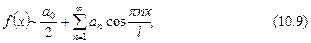
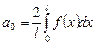 ,
, 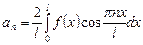 . (10.10)
. (10.10)
 . (10.12)
. (10.12)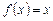 , – 2
, – 2 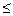 x
x 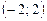 , то при разложении ее в ряд Фурье воспользуемся формулами (10.11), (10.12), где полагаем l = 2:
, то при разложении ее в ряд Фурье воспользуемся формулами (10.11), (10.12), где полагаем l = 2: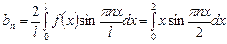 .
.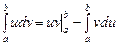 , положив u = x, dv=
, положив u = x, dv= 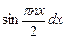 .
. dx
dx 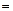 dx,
dx,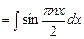
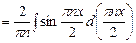



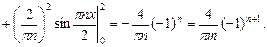
 .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
.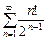 . 6.
. 6. 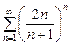 . 7.
. 7.  .
.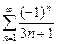 . 9.
. 9. 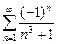 .
.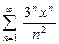 . 11.
. 11. 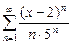 .
.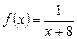 . 13.
. 13.  .
.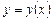 дифференциального уравнения
дифференциального уравнения 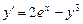 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 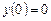 .
.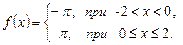
 ; б)
; б)  ;
в)
;
в)  ;г)
;г)  .
.
 называется сходящимся, если
а)сходится последовательность частичных сумм; б)
называется сходящимся, если
а)сходится последовательность частичных сумм; б)  ;в)
;в)  ; г) остаток ряда при
; г) остаток ряда при 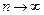 стремится к
стремится к  .
.
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
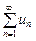 (un
(un  0)
0) 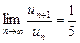 , то этот ряд а)сходится;б)монотонно убывает;
в)расходится; г)условно сходится.
, то этот ряд а)сходится;б)монотонно убывает;
в)расходится; г)условно сходится.
 равен
равен  , то интервалом сходимости этого ряда является интервал
а)
, то интервалом сходимости этого ряда является интервал
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
 где
где  ; б)
; б)  где
где
 ;в)
;в)  где
где  ;
г)
;
г)  где
где  .
.



