
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 14. Теория вероятностейСодержание книги
Поиск на нашем сайте
1. Элементы комбинаторики. [1], ч. 5, разд. 1, § 1. 2. Основные понятия теории вероятностей: события, классификация событий. Операции сложения и умножения событий. [1], ч. 5, разд. 1, § 1. 3. Вероятность события: статистическое, классическое и геометрическое определения вероятностей событий. [1], ч. 5, разд. 1, § 1, 2. 4. Основные аксиомы теории вероятностей. Непосредственное вычисление вероятностей событий. [1], ч. 5, разд. 1, § 1. 5. Теоремы сложения и умножения вероятностей.[1], ч.5,разд.1, §2. 6. Формула полной вероятности. Формула Байеса.[1],ч.5,разд.1,§ 3. 7. Повторение испытаний. Формула Бернулли. Локальная и интегральная теоремы Лапласа. [1], ч. 5, разд. 1, § 3, 8. 8. Случайная величина. Закон распределения дискретной случай-ной величины, его свойства. [1], ч. 5, разд. 1, § 4. 9. Интегральная функция распределения случайной величины, ее свойства. [1], ч. 5, разд. 1, § 4. 10. Дифференциальная функция (плотность) распределения и ее свойства. [1], ч. 5, разд. 1, § 4. 11. Числовые характеристики распределения случайных величин: математическое ожидание, дисперсия, их свойства. Среднее квадратическое отклонение. [1], ч. 5, разд. 1, § 5. 12. Законы распределения случайных величин: биномиальный, Пуассона, равномерный и экспоненциальный. Распределение Стьюдента. Их числовые характеристики. [1], ч. 5, разд. 1, § 6. 13. Нормальный закон распределения. [1], ч. 5, разд. 1, § 7. 14. Системы случайных величин. Закон распределения систем. Понятие условного закона распределения. [1], ч.5, разд. 1, § 10. 15. Числовые характеристики распределения двумерной случайной величины, корреляционный момент, его свойства. [1], ч. 5, разд. 1, § 10. 16. Закон больших чисел. [1], ч. 5, разд. 1, § 8.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 11. Высшая математика для инженеров. В 2 т. Т.2: Учеб. пособие для вузов/ С.А. Минюк, Н.С. Березкина, А.В. Метельский; Под общ. ред. Н.А. Микулика. Мн.: ООО «Элайда», 2004 – 592 с. 12. Гусак А. А. Высшая математика. – Мн.: Тетра Системс, 1998. 13. Индивидуальные задания по высшей математике. 3 часть/ Под. ред. А.П. Рябушко. – Мн.: Вышэйшая школа, 2004 (второе издание). 14. Пискунов Н.С. Дифференциальное и интегральное исчисление. М.: Наука, 1985. – Т. 2. 15. Бермант А. Ф., Араманович И. Г. Краткий курс математического анализа. – М.:Наука, 1985. 16. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. – Мн.: Вышейшая школа, 1986. – Ч. 2. 17. Элементы теории поля. Методические указания для студентов агроэнергетического факультета. Мн.: БГАТУ, 1999. 18. Лихолетов И. И., Мацкевич И. П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. – Мн.: Вышейшая школа, 1976. 19. Сборник индивидуальных заданий по теории вероятности и математической статистике. – Мн.: Вышэйшая школа, 1992. 20. Жевняк Р.М., Карпук А.А. Общий курс высшей математики. – Орша, 1996.
Модуль 11. ДВОЙНОЙ ИНТЕГРАЛ Двойной интеграл и его свойства Пусть функция
Эта сумма называется Диаметром области Определение. Если существует конечный предел последовательности интегральных сумм
Теорема существования. Если функция Свойства двойного интеграла 1. 2. 3. Если область интегрирования
Вычисление двойного интеграла В прямоугольных декартовых координатах В прямоугольной системе координат элемент площади
Область Например, область
Рис. 11.1
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.006 с.) |

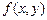 определена в некоторой замкнутой области
определена в некоторой замкнутой области  плоскости
плоскости  . Разобьем область
. Разобьем область 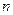 частей
частей  с площадями
с площадями 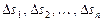 . Внутри каждой элементарной области
. Внутри каждой элементарной области 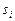 выберем произвольную точку
выберем произвольную точку  и найдем значение функции
и найдем значение функции 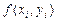 в этой точке. Составим сумму:
в этой точке. Составим сумму: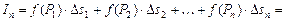
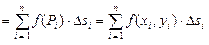
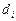 .
.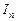 при стремлении к нулю наибольшего из диаметров частичных областей
при стремлении к нулю наибольшего из диаметров частичных областей  , то он называется двойным интегралом от функции
, то он называется двойным интегралом от функции 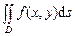 . Таким образом,
. Таким образом,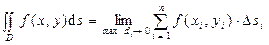

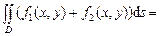
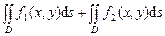 .
. и
и 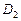 без общих внутренних точек, то
без общих внутренних точек, то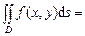
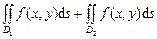 .
.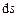 можно записать в виде произведения
можно записать в виде произведения  . Тогда
. Тогда .
.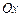 (или
(или 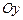 ), если любая прямая, проходящая параллельно этой оси, пересекает границу области
), если любая прямая, проходящая параллельно этой оси, пересекает границу области 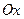 (прямая
(прямая  пересекает границу области
пересекает границу области 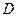 в четырех точках).
в четырех точках).




