
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль и аргумент комплексного числа. Тригонометрическая и показательнаяСодержание книги
Поиск на нашем сайте
Формы комплексного числа Модулем комплексного числа
и обозначается Угол
Очевидно, что аргумент комплексного числа определяется неоднозначно, а с точностью до слагаемого
Подставим в алгебраическую форму комплексного числа Получим формулу
которая называется тригонометрической формой комплексного числа. Обозначив символом
запишем комплексное число (8.2) в показательной форме Таким образом, комплексное число имеет 3 формы записи:
где Формулы Эйлера Заменяя в формуле
Складывая и вычитая равенства (8.3) и (8.4), находим
Формулы (8.3) и (8.4) называются формулами Эйлера. Эти формулы связывают показательную и тригонометрические функции. Пример 8.1. Следующие комплексные числа представить в тригонометрической и показательной формах и изобразить точками и векторами на комплексной плоскости: а) Решение. а) Действительная и мнимая части комплексного числа равны Найдем модуль и аргумент
Следовательно, представление комплексного числа
Числа Действия над комплексными числами Если комплексные числа заданы в алгебраической форме 1. 2. 3. 4.
при этом Пример 8.2. Даны комплексные числа:
Вычислить: 1) Решение. 1) Последовательно вычислим
Тогда 2) Аналогично вычисляем
Тогда 3) Вычисляем
Тогда Операции умножения и деления удобно проводить и над числами, заданными в тригонометрической или показательной формах (см.[1], гл. VII, § 2,3).
Применение комплексных чисел в электротехнике
Рассмотрим синусоидальный ток, закон изменения которого во времени описывается формулой
где График тока дан на рис. 8.3.
При расчете цепей синусоидального тока используется также понятие действующего значения тока
Для облегчения расчетов в электротехнике синусоидальный ток принято изображать вектором (или точкой) на комплексной плоскости
который называется комплексной амплитудой (рис. 8.4). (обратите внимание на обозначения осей координат!). Модуль этого вектора равен амплитуде Если комплексную амплитуду разделить на
Зная комплексную амплитуду или комплексное действующее значение синусоидальной величины, можно осуществить обратный переход и записать выражение для мгновенного значения этой величины. Пример 8.3. Ток меняется по закону
По формуле (8.5) находим комплексную амплитуду:
Комплексная амплитуда изображена на рис. 8.5. Пример 8.4. Задано комплексное действующее значение тока Решение. Найдем действующее значение
Амплитуда
Определим начальную фазу Поскольку число
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 1. Даны комплексные числа Найти число 2. Представить в тригонометрической и показательной формах и изобразить на комплексной плоскости следующие комплексные числа: а) 3. Решить уравнения а) 4. Ток меняется по закону
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.104.128 (0.01 с.) |

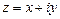 называется число
называется число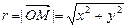
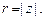
 , образованный вектором
, образованный вектором 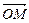 с положительным направлением оси Ох, называется аргументом комплексного числа и обозначается
с положительным направлением оси Ох, называется аргументом комплексного числа и обозначается 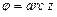 . Аргумент
. Аргумент 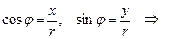 tg
tg 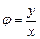 .
.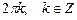 . Главное значение аргумента
. Главное значение аргумента 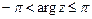 или
или 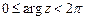 .
. .
.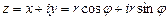 , или
, или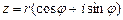 , (8.2)
, (8.2)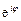 комплексное число
комплексное число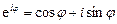 ,
,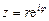 .
.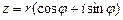 – тригонометрическая форма,
– тригонометрическая форма, 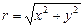 – модуль комплексного числа,
– модуль комплексного числа,  – аргумент комплексного числа, tg
– аргумент комплексного числа, tg  .
.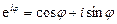 (8.3)
(8.3) . (8.4)
. (8.4)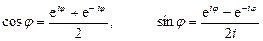 .
. , б)
, б) 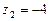 .
.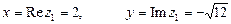
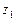 :
: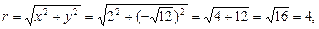
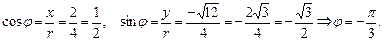
 и
и 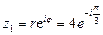 .
. б)
б) 
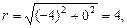

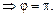 Таким образом,
Таким образом,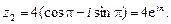
 изображены на рис. 8.2.
изображены на рис. 8.2.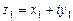 ,
, 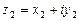 , то операции сложения, вычитания, умножения и деления этих чисел выполняются по следующим правилам:
, то операции сложения, вычитания, умножения и деления этих чисел выполняются по следующим правилам:
 ,
,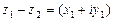
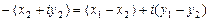 ,
,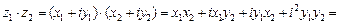
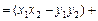
 ,
,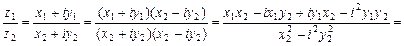
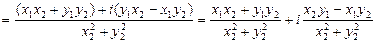 ,
,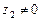 .
. ,
, 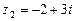 ,
, 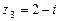 .
.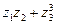 ; 2)
; 2) 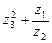 ; 3)
; 3)  .
.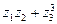 :
:
 .
.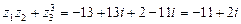 .
.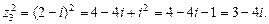

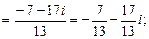

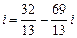 .
.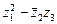 :
: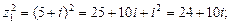
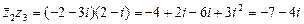 .
. .
.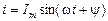 ,
,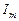 – амплитуда тока, характеризует максимальное значение тока,
– амплитуда тока, характеризует максимальное значение тока, 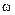 – угловая частота,
– угловая частота,  – фаза, характеризует состояние колебания в момент времени
– фаза, характеризует состояние колебания в момент времени 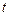 ,
, 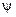 – начальная фаза.
– начальная фаза.

 .
.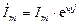
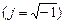 , (8.5)
, (8.5) , а аргумент – начальной фазе
, а аргумент – начальной фазе 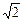 , то получим комплексное действующее значения тока
, то получим комплексное действующее значения тока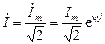 .
. А. Найти комплексную амплитуду тока и изобразить ее на комплексной плоскости.
А. Найти комплексную амплитуду тока и изобразить ее на комплексной плоскости. Решение. Из условия находим амплитуду
Решение. Из условия находим амплитуду  .
.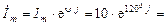

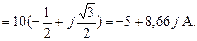
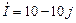 А. Записать выражение для его мгновенного значения.
А. Записать выражение для его мгновенного значения.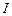 тока как модуль комплексного действующего значения
тока как модуль комплексного действующего значения  тока:
тока: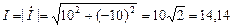 А.
А.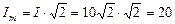 А.
А.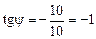 .
.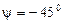 . Записываем выражение для мгновенного значения синусоидального тока:
. Записываем выражение для мгновенного значения синусоидального тока: А.
А.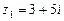 ,
,  ,
, 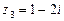 .
. .
.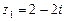 ; б)
; б)  ; в)
; в) 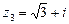 .
. ; б)
; б) 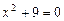 .
.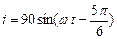 А.Найти комплексную амплитуду
А.Найти комплексную амплитуду 


