
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи математической статистики.Содержание книги
Поиск на нашем сайте
Первая задача – указать способы сбора и группировки статистических данных. Вторая задача – разработать методы анализа и обработки полученных статистических данных в зависимости от целей исследований. Определение. Совокупность N объектов, из которых производится выборка объектов для исследования, называется генеральной совокупностью. Определение. Совокупность п объектов, случайно отобранных из генеральной совокупности, называется выборочной совокупностью или выборкой ( Определение. Выборка называется бесповторной, если отобранный для исследования случайным образом объект в генеральную совокупность не возвращается. Определение. Выборка называется повторной, если отобранный случайным образом объект перед отбором следующего объекта возвращается в генеральную совокупность. Для того, чтобы выборка давала правильное представление о генеральной совокупности, она должна быть представительной или репрезентативной, т.е. для каждого объекта генеральной совокупности вероятность попасть в выборку одна и та же. Пусть совокупность объектов Определение. Наблюдаемые значения Определение. Числа Определение. Статистическим распределением выборки называется задание вариант и соответствующих им частот или относительных частот. Определение. Таблица
или
называется статистическим рядом. Пусть изучается генеральная совокупность относительно некоторого признака Х. Пусть Определение. Генеральной средней
Если же не все значения различны, а различные значения
Предположим, что все объекты генеральной совокупности объема
Итак, генеральная средняя есть математическое ожидание рассматриваемого признака Х. Пусть требуется изучить генеральную совокупность объема Определение. Выборочной средней
Если не все значения признака различны, то
Если из генеральной совокупности извлечена выборка, то она имеет выборочную среднюю, которая является определенным числом. Другая выборка, извлеченная из генеральной совокупности, будет иметь свою выборочную среднюю, которую можно рассматривать как случайную величину, а следовательно, можно говорить о распределении выборочной средней и о ее числовых характеристиках. Замечание. В теоретических рассуждениях выборочные значения признака Х рассматриваются как случайные величины, имеющие то же распределение и те же числовые характеристики, что и признак Х. Рассмотрим генеральную совокупность объема Определение. Генеральной дисперсией
Если же не все значения признака различны, т.е.
Средним квадратическим отклонением генеральной совокупности называется
Пусть требуется изучить генеральную совокупность объема Определение. Выборочной дисперсией
Если же не все значения признака различны, то Средним квадратическим отклонением выборочной совокупности называется
Пусть известно статистическое распределение некоторого признака Х:
Пусть х – некоторое действительное число. Обозначим Тогда Определение. Статистической (эмпирической) функцией распределения называется функция
Статистическая функция Различие между этими функциями состоит в том, что Функция 1. 2. 3. Если В целях наглядности строят графики статистического распределения выборки. Определение. Полигоном частот называется ломаная линия с вершинами в точках Полигоном относительных частот называется ломаная линия с вершинами в точках
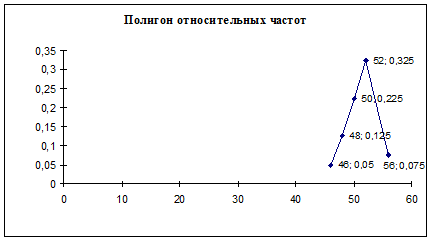
Пример 14.23. В магазине было продано за день 40 костюмов. Имеется вариационный ряд случайной величины Х- размера костюма.
Построить полигон относительных частот. Решение. Составим ряд относительных частот.
Проверка:
Определение. Гистограммой частот (относительных частот) называется ступенчатая фигура, состоящая из прямоугольников, основаниям которых служат отрезки длины Значения длин Если в генеральной совокупности признак имеет дискретное значение, то промежуток в котором находятся варианты разбиваем на части так, чтобы на каждом участке была одна варианта. Пример 14.23. Стадо коров в 1000 голов обследуется на жирность молока. Для обследования случайным образом отобрано 50 коров. Объем генеральной совокупности При этом получено статистическое распределение:
Составить ряд распределения относительных частот Решение. Так как нам известно, что,то статистический ряд распределения относительных частот имеет вид
Составим статистическую функцию распределения
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 1. В группе студентов, состоящей из 20человек, 12 юношей и 8 девушек. Для поездки на сельхозработы случайным образом отобрано двое студентов. Какова вероятность того, что среди них будет а) 2 юноши; б) один юноша и одна девушка? 2. Три стрелка производят выстрел по цели. Вероятность попадания в цель для первого стрелка равна 0,6, для второго – 0,8, для третьего – 0,9. Найти вероятность того, что произойдет не менее двух попаданий. 3. Электрическая цепь состоит из пяти, работающих независимо друг от друга. Определить надежность работы цепи, если надежность работы каждого элемента pi указана на рисунке
р1 = 0,9, р2 = 0,81, р3 = 0,82, р4 = 0,85, р5 = 0,94. 4. На сборку поступают шестерни с 3-х автоматов. Первый дает 25%, второй – 30% и третий – 45% шестерен, поступающих на сборку. Первый автомат допускает 0,1% брака шестерен, второй–0,2%. третий – 0,3%. Найти вероятность поступления на сборку бракованной шестерни. 5. В ремонтной мастерской имеются 4 мотора. Для каждого мотора вероятность того, что он включен, равна 0,9. Найти вероятность того, что в данный момент а) включено 3 мотора; б) включен хотя бы один мотор; в) включено не менее трех моторов. 6. Срок службы шестерен коробок передач зависит от следующих факторов: усталости материала в основании зуба, контактных напряжений и жесткости конструкции. Вероятность отказа каждого фактора в одном испытании не зависит от влияния остальных факторов и равна 0,1. Составить закон распределения числа отказавших факторов в одном испытании. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х – числа отказов факторов. 7. Случайная величина Х задана интегральной функцией
Найти а) дифференциальную функцию распределения; б) вероятность того, что случайная величина Х примет значение в интервале 8. Случайная величина Х задана дифференциальной функцией
Найти числовые характеристики случайной величины Х. 9. Случайная величина Х имеет равномерное распределение на интервале (-1, 1). Написать выражение для плотности вероятности, найти математическое ожидание и дисперсию случайной величины. 10. В каком случае верно составлен ряд распределения случайной величины Х?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.251 (0.011 с.) |

 ).
).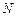 исследуется по некоторому признаку Х. Произведем выборку объема п. Пусть в результате эксперимента случайная величина Х приняла значения
исследуется по некоторому признаку Х. Произведем выборку объема п. Пусть в результате эксперимента случайная величина Х приняла значения  раз,
раз,  раз, …,
раз, …,  раз, причем
раз, причем 
 называется вариантами, а последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.
называется вариантами, а последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом. называется частотами, числа
называется частотами, числа  называются относительными частотами,
называются относительными частотами, 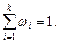



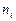

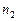





 – возможные значения этого признака, причем все различные.
– возможные значения этого признака, причем все различные. называется среднее арифметическое возможного значения
называется среднее арифметическое возможного значения
 раз,
раз,  раз, …,
раз, …,  раз, тогда
раз, тогда .
. признаком, равна
признаком, равна  . Тогда
. Тогда .
.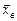 называется среднее арифметическое значений признака выборочной совокупности
называется среднее арифметическое значений признака выборочной совокупности .
.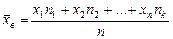 .
.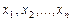 - значения количественного признака Х – различны.
- значения количественного признака Х – различны. называется среднее арифметическое квадратов отклонений значений признака
называется среднее арифметическое квадратов отклонений значений признака 
 .
. .
.
 называется среднее арифметическое квадратов отклонений значений признака
называется среднее арифметическое квадратов отклонений значений признака 
 .
. .
.
 - сумму частот, варианты которых меньше х.
- сумму частот, варианты которых меньше х. – относительная частота события
– относительная частота события 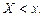
 .
. сходственна с интегральной функцией распределения
сходственна с интегральной функцией распределения  , которую в математической статистике называют теоретической функцией распределения.
, которую в математической статистике называют теоретической функцией распределения.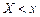 ,
, 
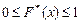 .
. то
то  то
то 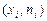 .
. .
.



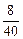

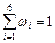 .
. , лежащие на оси Ох, а высотами –отрезки длиной
, лежащие на оси Ох, а высотами –отрезки длиной 
 .
. -ом отрезке.
-ом отрезке. Объем выборки п =50.
Объем выборки п =50.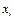 % жирности
% жирности

 . Записать статистическую функцию распределения
. Записать статистическую функцию распределения  % жирности
% жирности







 .
.



