

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Контрольный тест по модулю №14
| 10.Вероятность Р случайного события А удовлетворяет условию
а) Р (А)=0;б) Р (А)=1;в) Р (А)>1;г)0< Р (А)<1.
| | 20.Какова вероятность выпадения очка равного 3 при одном бросании игрального кубика?
а)1;б)1/6;в)1/3;г)2/3.
| 3.Цепь работает по схеме 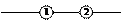  . Работа каждого элемента является независимым событием, вероятность которого равна 0,8. Найти вероятность работы цепи. . Работа каждого элемента является независимым событием, вероятность которого равна 0,8. Найти вероятность работы цепи.
| 4.Вероятность события А при наступлении хотя бы одного события Нi (i =1, 2, …, n)из полной группы событий находится по формуле:
а) 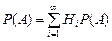 ; б) ; б) 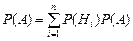 ;
в) ;
в) 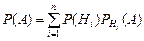 ;г) ;г)  . .
| 5.Если монету бросают 7 раз, то вероятность выпадения герба в 5 случаях вычисляется по формуле:
а) 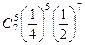 ;б) ;б)  ; в) ; в)  ;г) ;г)  . .
| | 6.Какое свойство математического ожидания не выполняется?
а) М [ X+Y ]= M [ X ]+ M [ Y ]; б) М [ X∙Y ]= M [ X ]∙ M [ Y ];
в) М [ CX ]= CX; г) М [ X - М [ X ]]= 0.
| 7. Заполните пустую клетку ряда распределения случ. величины Х
| | 8.Вычислите математическое ожидание случайной величины из задания 7.
| 9*. Если случайная величина Х – число выпадения герба при 3 бросаниях монеты, то ее дисперсия 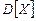 равна
а)1;б)0,5;в)0,75;г)0,8. равна
а)1;б)0,5;в)0,75;г)0,8.
| 10*.Станок изготавливает за смену 100000 деталей. Вероятность изготовления бракованной детали рана 0,0001. Если случайная величина Х-число бракованных деталей за смену среди 5 отобранных деталей, то ее дисперсия 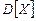 равна
а)1;б)10; в)12; г)18. равна
а)1;б)10; в)12; г)18.
|
Итоговый КОНТРОЛЬНЫЙ ТЕСТ №4
10.Какое свойство справедливо для двойного интеграла (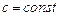 )?
а) )?
а)  б) б) 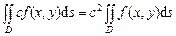 ;
в) ;
в)  ; г) ; г) 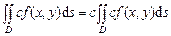 . .
| 20. Интеграл вида  является:
а)определенным интегралом;б) неопределенным интегралом;
в) криволинейным интегралом 2-го рода;
г) суммой двух определенных интегралов. является:
а)определенным интегралом;б) неопределенным интегралом;
в) криволинейным интегралом 2-го рода;
г) суммой двух определенных интегралов.
| | 30.Вероятность Р невозможного события В удовлетворяет условию
а) Р (В)=0; б) Р (В)=1; в) Р (В)>1; г) 0< Р (В)<1.
| 40.Как называется векторное поле  , если в каждой его точке , если в каждой его точке  и и 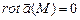 ?
а)потенциальное;б)гармоническое;
в)трубчатое; г)соленоидальное. ?
а)потенциальное;б)гармоническое;
в)трубчатое; г)соленоидальное.
| | 50. Какова вероятность извлечения туза из колоды 36 карт?
а)1/36;б)1/6; в)1/9; г)2/3.
| 6.Вычислить двойной интеграл 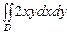 , если область , если область  задается неравенствами задается неравенствами  , ,  . .
| 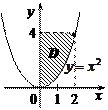 7.Если в двойном интеграле 7.Если в двойном интеграле  , где область , где область  изображена на рисунке, перейти к повторному интегралу, то он имеет вид
а) изображена на рисунке, перейти к повторному интегралу, то он имеет вид
а)  ; б) ; б)  ;
в) ;
в)  ; г) ; г)  . .
| 8.Вычислить криволинейный интеграл  , по дуге L: , по дуге L: 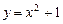 от точки от точки  до точки до точки 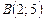 .
а)0; б)1;в)4;г)2. .
а)0; б)1;в)4;г)2.
|  9.Площадь фигуры, изображенной на рисунке, находится с помощью интеграла
а) 9.Площадь фигуры, изображенной на рисунке, находится с помощью интеграла
а)  ;б) ;б)  ;
в) ;
в)  ; г) ; г) 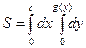 . .
| 10.Если игральную кость бросают 7 раз, то вероятность выпадения очка равного 5 в 4 случаях вычисляется по формуле:
а) 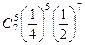 ;б) ;б) 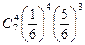 ;в) ;в)  ;г) ;г) 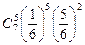 . .
| | 11. Какое свойство справедливо для функции распределения F (x) случайной величины Х?
а) F (-∞)=1; б) F (+∞)=0; в) F( +∞)=1; г) F (+∞)=-1.
| 12. Если плотность случайной величины вычисляется по формуле 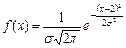 , то математическое ожидание , то математическое ожидание 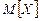 данной случайной величины равно… данной случайной величины равно…
| 13*.Какое из выражений является полным дифференциалом?
а)  ; б) ; б)  ;
в) ;
в)  ;г) ;г)  . .
| 14*.Найти работу силы  вдоль окружности вдоль окружности 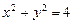 в положительном направлении. в положительном направлении.
| 15*. Для функции  найти найти 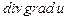 .
а) .
а) 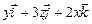 ; б) ; б) 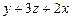 ;в)0;г) 6. ;в)0;г) 6.
| 16*. Цепь работает по схеме 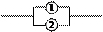  . Работа каждого элемента является независимым событием, вероятность которого равна 0,5. Найти вероятность работы системы.
а)0,75;б)0,25;в)0,125; г)1,25. . Работа каждого элемента является независимым событием, вероятность которого равна 0,5. Найти вероятность работы системы.
а)0,75;б)0,25;в)0,125; г)1,25.
|
КРАТКИЙ СПРАВОЧНИК
Интегрирование некоторых типов дифференциальных
Уравнений (ДУ) первого порядка
Таблица 1
| Тип уравнения
| Метод решения
| Простейшее ДУ первого порядка
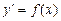
| Проинтегрировать правую часть
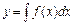 + C + C
| ДУ с разделенными
переменными
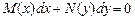
| Почленно проинтегрировать

| ДУ с разделяющимися
переменными

| «Разделить» переменные, разделив уравнение на 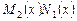 и
проинтегрировать и
проинтегрировать 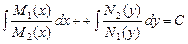
| Однородное ДУ первого порядка
 , где , где 
| Решается заменой 
| Линейное ДУ 1-ого порядка
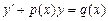
| Решается заменой 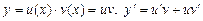
| ДУ Бернулли
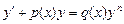 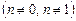
| Решается заменой 
|
Интегрирование некоторых типов дифференциальных
Уравнений (ДУ) второго порядка
Таблица 2
| Тип уравнения
| Метод решения
| Простейшее ДУ 2-го порядка
а)  б)
б)  в)
в) 
| а)Произвести двукратное интегрирова-ние правой части  б) Решается заменой
б) Решается заменой  в)Решается заменой
в)Решается заменой
 
| Линейное однородное ДУ 2-ого порядка с постоянными коэффициентами

| Находим корни  характеристичес-кого уравнения: характеристичес-кого уравнения:  . Если . Если
| 1) 
| 
| 2) 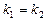
| 
| 3) 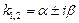 – комплексные – комплексные
| 
| Линейное неоднород-ное ДУ 2-ого порядка с постоянными коэффи-циентами

| Найти общее решение  соответству-ющего линейного однородного ДУ и одно из частных решений соответству-ющего линейного однородного ДУ и одно из частных решений  линейного неоднородного ДУ ( линейного неоднородного ДУ ( находится спомощью таблицы 2 (продолжение)
Тогда общее решение имеет вид находится спомощью таблицы 2 (продолжение)
Тогда общее решение имеет вид
 . .
| Вид частного решения 
линейного неоднородного уравнения 
Продолжение таблицы 2
| f(x)
|
| y*
| | 1. Pn(x)
| a) 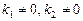
| Qn(x)
| б)  или или 
| x Qn(x)
| в) 
| x2 Qn(x)
| | 2. A eαx
| a) 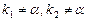
| B eαx
| б) 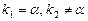 или или 
| B x eαx
| в) 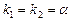
| B x2 eαx
| | 3. eαx Pn(x)
| a) 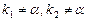
| eαx Qn(x)
| б) 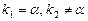 или или 
| x eαx Qn(x)
| в) 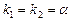
| x2 eαx Qn(x)
| | 4. Pn(x) cos βx или
Rn(x) sin βx
| a) 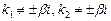
| Qn(x) cos(βx)+ Sn(x) sin(βx)
| б) 
| x(Qn(x) cos(βx)+ Sn(x) sin(βx))
| | 5. eαx Pn(x) cos βx
или
eαx Rn(x) sin βx
| a) 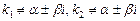
| eαx (Qn(x) cos(βx)+ Sn(x) sin(βx))
| б) 
| xeαx(Qn(x) cos(βx)+ Sn(x) sin(βx))
| | 6. eαx (Pl(x) cos βx+
Rm(x) sin βx)
| a) 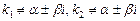
| eαx (Qn(x) cos(βx)+ Sn(x) sin(βx))
| б) 
| xeαx(Qn(x) cos(βx)+ Sn(x) sin(βx))
n=max(l,m)
| Где Pn(x), Qn(x), Rn(x), Sn(x) – многочлены степени n, причем P0(x)=A,
P1(x)=Ax+B,
P2(x)=Ax2+Bx+C, где A, B, C – некоторые действительные числа.
Таблица значений функции 
Таблица 3
| |
|
|
|
|
|
|
|
|
|
| | 0,0
| 0,3989
|
|
|
|
|
|
|
|
|
| | 0,1
|
|
|
|
|
|
|
|
|
|
| | 0,2
|
|
|
|
|
|
|
|
|
|
| | 0,3
|
|
|
|
|
|
|
|
|
|
| | 0,4
|
|
|
|
|
|
|
|
|
|
| | 0,5
|
|
|
|
|
|
|
|
|
|
| | 0,6
|
|
|
|
|
|
|
|
|
|
| | 0,7
|
|
|
|
|
|
|
|
|
|
| | 0,8
|
|
|
|
|
|
|
|
|
|
| | 0,9
|
|
|
|
|
|
|
|
|
|
| | 1,0
| 0,2420
|
|
|
|
|
|
|
|
|
| | 1,1
|
|
|
|
|
|
|
|
|
|
| | 1,2
|
|
|
|
|
|
|
|
|
|
| | 1,3
|
|
|
|
|
|
|
|
|
|
| | 1,4
|
|
|
|
|
|
|
|
|
|
| | 1,5
|
|
|
|
|
|
|
|
|
|
| | 1,6
|
|
|
|
|
|
|
|
|
|
| | 1,7
|
|
|
|
|
|
|
|
|
|
| | 1,8
|
|
|
|
|
|
|
|
|
|
| | 1,9
|
|
|
|
|
|
|
|
|
|
| | 2,0
| 0,0540
|
|
|
|
|
|
|
|
|
| | 2,1
|
|
|
|
|
|
|
|
|
|
| | 2,2
|
|
|
|
|
|
|
|
|
|
| | 2,3
|
|
|
|
|
|
|
|
|
|
| | 2,4
|
|
|
|
|
|
|
|
|
|
| | 2,5
|
|
|
|
|
|
|
|
|
|
| | 2,6
|
|
|
|
|
|
|
|
|
|
| | 2,7
|
|
|
|
|
|
|
|
|
|
| | 2,8
|
|
|
|
|
|
|
|
|
|
| | 2,9
|
|
|
|
|
|
|
|
|
|
| | 3,0
| 0,0044
|
|
|
|
|
|
|
|
|
| | 3,1
|
|
|
|
|
|
|
|
|
|
| | 3,2
|
|
|
|
|
|
|
|
|
|
| | 3,3
|
|
|
|
|
|
|
|
|
|
| | 3,4
|
|
|
|
|
|
|
|
|
|
| | 3,5
|
|
|
|
|
|
|
|
|
|
| | 3,6
|
|
|
|
|
|
|
|
|
|
| | 3,7
|
|
|
|
|
|
|
|
|
|
| | 3,8
|
|
|
|
|
|
|
|
|
|
| | 3,9
|
|
|
|
|
|
|
|
|
|
| Таблица значений функции  . .
Таблица 4
| x
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| | 0,00
| 0,0000
| 0,32
| 0,1255
| 0,64
| 0,2389
| 0,96
| 0,3315
| | 0,01
| 0,0040
| 0,33
| 0,1293
| 0,65
| 0,2422
| 0,97
| 0,3340
| | 0,02
| 0,0080
| 0,34
| 0,1331
| 0,66
| 0,2454
| 0,98
| 0,3365
| | 0,03
| 0,0120
| 0,35
| 0,1368
| 0,67
| 0,2486
| 0,99
| 0,3389
| | 0,04
| 0,0160
| 0,36
| 0,1406
| 0,68
| 0,2517
| 1,00
| 0,3413
| | 0,05
| 0,0199
| 0,37
| 0,1443
| 0,69
| 0,2549
| 1,01
| 0,3438
| | 0,06
| 0,0239
| 0,38
| 0,1480
| 0,70
| 0,2580
| 1,02
| 0,3461
| | 0,07
| 0,0279
| 0,39
| 0,1517
| 0,71
| 0,2611
| 1,03
| 0,3485
| | 0,08
| 0,0319
| 0,40
| 0,1554
| 0,72
| 0,2642
| 1,04
| 0,3508
| | 0,09
| 0,0359
| 0,41
| 0,1591
| 0,73
| 0,2673
| 1,05
| 0,3531
| | 0,10
| 0,0398
| 0,42
| 0,1628
| 0,74
| 0,2703
| 1,06
| 0,3554
| | 0,11
| 0,0438
| 0,43
| 0,1664
| 0,75
| 0,2734
| 1,07
| 0,3577
| | 0,12
| 0,0478
| 0,44
| 0,1700
| 0,76
| 0,2764
| 1,08
| 0,3599
| | 0,13
| 0,0517
| 0,45
| 0,1736
| 0,77
| 0,2794
| 1,09
| 0,3621
| | 0,14
| 0,0557
| 0,46
| 0,1772
| 0,78
| 0,2823
| 1,10
| 0,3643
| | 0,15
| 0,0596
| 0,47
| 0,1808
| 0,79
| 0,2852
| 1,11
| 0,3665
| | 0,16
| 0,0636
| 0,48
| 0,1844
| 0,80
| 0,2881
| 1,12
| 0,3686
| | 0,17
| 0,0675
| 0,49
| 0,1879
| 0,81
| 0,2910
| 1,13
| 0,3708
| | 0,18
| 0,0714
| 0,50
| 0,1915
| 0,82
| 0,2939
| 1,14
| 0,3729
| | 0,19
| 0,0753
| 0,51
| 0,1950
| 0,83
| 0,2967
| 1,15
| 0,3749
| | 0,20
| 0,0793
| 0,52
| 0,1985
| 0,84
| 0,2995
| 1,16
| 0,3770
| | 0,21
| 0,0832
| 0,53
| 0,2019
| 0,85
| 0,3023
| 1,17
| 0,3790
| | 0,22
| 0,0871
| 0,54
| 0,2054
| 0,86
| 0,3051
| 1,18
| 0,3810
| | 0,23
| 0,0910
| 0,55
| 0,2088
| 0,87
| 0,3078
| 1,19
| 0,3830
| | 0,24
| 0,0948
| 0,56
| 0,2123
| 0,88
| 0,3106
| 1,20
| 0,3849
| | 0,25
| 0,0987
| 0,57
| 0,2157
| 0,89
| 0,3133
| 1,21
| 0,3869
| | 0,26
| 0,1026
| 0,58
| 0,2190
| 0,90
| 0,3159
| 1,22
| 0,3883
| | 0,27
| 0,1064
| 0,59
| 0,2224
| 0,91
| 0,3186
| 1,23
| 0,3907
| | 0,28
| 0,1103
| 0,60
| 0,2257
| 0,92
| 0,3212
| 1,24
| 0,3925
| | 0,29
| 0,1141
| 0,61
| 0,2291
| 0,93
| 0,3238
| 1,25
| 0,3944
| | 0,30
| 0,1179
| 0,62
| 0,2324
| 0,94
| 0,3264
|
|
| | 0,31
| 0,1217
| 0,63
| 0,2357
| 0,95
| 0,3289
|
|
|
Продолжение таблицы 4
| x
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| | 1,26
| 0,3962
| 1,59
| 0,4441
| 1,92
| 0,4726
| 2,50
| 0,4938
| | 1,27
| 0,3980
| 1,60
| 0,4452
| 1,93
| 0,4732
| 2,52
| 0,4941
| | 1,28
| 0,3997
| 1,61
| 0,4463
| 1,94
| 0,4738
| 2,54
| 0,4945
| | 1,29
| 0,4015
| 1,62
| 0,4474
| 1,95
| 0,4744
| 2,56
| 0,4948
| | 1,30
| 0,4032
| 1,63
| 0,4484
| 1,96
| 0,4750
| 2,58
| 0,4951
| | 1,31
| 0,4049
| 1,64
| 0,4495
| 1,97
| 0,4756
| 2,60
| 0,4953
| | 1,32
| 0,4066
| 1,65
| 0,4505
| 1,98
| 0,4761
| 2,62
| 0,4956
| | 1,33
| 0,4082
| 1,66
| 0,4515
| 1,99
| 0,4767
| 2,64
| 0,4959
| | 1,34
| 0,4099
| 1,67
| 0,4525
| 2,00
| 0,4772
| 2,66
| 0,4961
| | 1,35
| 0,4115
| 1,68
| 0,4535
| 2,02
| 0,4783
| 2,68
| 0,4963
| | 1,36
| 0,4131
| 1,69
| 0,4545
| 2,04
| 0,4793
| 2,70
| 0,4965
| | 1,37
| 0,4147
| 1,70
| 0,4554
| 2,06
| 0,4803
| 2,72
| 0,4967
| | 1,38
| 0,4162
| 1,71
| 0,4564
| 2,08
| 0,4812
| 2,74
| 0,4969
| | 1,39
| 0,4177
| 1,72
| 0,4573
| 2,10
| 0,4821
| 2,76
| 0,4971
| | 1,40
| 0,4192
| 1,73
| 0,4582
| 2,12
| 0,4830
| 2,78
| 0,4673
| | 1,41
| 0,4207
| 1,74
| 0,4591
| 2,14
| 0,4838
| 2,80
| 0,4974
| | 1,42
| 0,4222
| 1,75
| 0,4599
| 2,16
| 0,4846
| 2,82
| 0,4976
| | 1,43
| 0,4236
| 1,76
| 0,4608
| 2,18
| 0,4854
| 2,84
| 0,4977
| | 1,44
| 0,4251
| 1,77
| 0,4616
| 2,20
| 0,4861
| 2,86
| 0,4979
| | 1,45
| 0,4265
| 1,78
| 0,4625
| 2,22
| 0,4868
| 2,88
| 0,4980
| | 1,46
| 0,4279
| 1,79
| 0,4633
| 2,24
| 0,4875
| 2,90
| 0,4981
| | 1,47
| 0,4292
| 1,80
| 0,4641
| 2,26
| 0,4881
| 2,92
| 0,4982
| | 1,48
| 0,4306
| 1,81
| 0,4649
| 2,28
| 0,4887
| 2,94
| 0,4984
| | 1,49
| 0,4319
| 1,82
| 0,4656
| 2,30
| 0,4893
| 2,96
| 0,4985
| | 1,50
| 0,4332
| 1,83
| 0,4664
| 2,32
| 0,4898
| 2,98
| 0,4986
| | 1,51
| 0,4345
| 1,84
| 0,4671
| 2,34
| 0,4904
| 3,00
| 0,49865
| | 1,52
| 0,4357
| 1,85
| 0,4678
| 2,36
| 0,4909
| 3,20
| 0,49931
| | 1,53
| 0,4370
| 1,86
| 0,4686
| 2,38
| 0,4913
| 3,40
| 0,49966
| | 1,54
| 0,4382
| 1,87
| 0,4693
| 2,40
| 0,4918
| 3,60
| 0,499841
| | 1,55
| 0,4394
| 1,88
| 0,4699
| 2,42
| 0,4922
| 3,80
| 0,499928
| | 1,56
| 0,4406
| 1,89
| 0,4706
| 2,44
| 0,4927
| 4,00
| 0,499968
| | 1,57
| 0,4418
| 1,90
| 0,4713
| 2,46
| 0,4931
| 4,50
| 0,499997
| | 1,58
| 0,4429
| 1,91
| 0,4719
| 2,48
| 0,4934
| 5,00
| 0,499997
|
ОТВЕТЫ
|



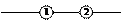
 . Работа каждого элемента является независимым событием, вероятность которого равна 0,8. Найти вероятность работы цепи.
. Работа каждого элемента является независимым событием, вероятность которого равна 0,8. Найти вероятность работы цепи.
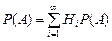 ; б)
; б) 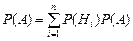 ;
в)
;
в) 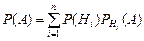 ;г)
;г)  .
.
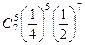 ;б)
;б)  ; в)
; в)  ;г)
;г)  .
.
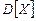 равна
а)1;б)0,5;в)0,75;г)0,8.
равна
а)1;б)0,5;в)0,75;г)0,8.
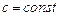 )?
а)
)?
а)  б)
б) 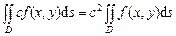 ;
в)
;
в)  ; г)
; г) 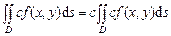 .
.
 является:
а)определенным интегралом;б) неопределенным интегралом;
в) криволинейным интегралом 2-го рода;
г) суммой двух определенных интегралов.
является:
а)определенным интегралом;б) неопределенным интегралом;
в) криволинейным интегралом 2-го рода;
г) суммой двух определенных интегралов.
 , если в каждой его точке
, если в каждой его точке  и
и 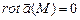 ?
а)потенциальное;б)гармоническое;
в)трубчатое; г)соленоидальное.
?
а)потенциальное;б)гармоническое;
в)трубчатое; г)соленоидальное.
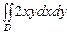 , если область
, если область  задается неравенствами
задается неравенствами  ,
,  .
.
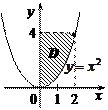 7.Если в двойном интеграле
7.Если в двойном интеграле  , где область
, где область  ; б)
; б)  ;
в)
;
в)  ; г)
; г)  .
.
 , по дуге L:
, по дуге L: 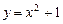 от точки
от точки  до точки
до точки 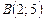 .
а)0; б)1;в)4;г)2.
.
а)0; б)1;в)4;г)2.
 9.Площадь фигуры, изображенной на рисунке, находится с помощью интеграла
а)
9.Площадь фигуры, изображенной на рисунке, находится с помощью интеграла
а)  ;б)
;б)  ;
в)
;
в)  ; г)
; г) 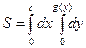 .
.
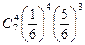 ;в)
;в)  ;г)
;г) 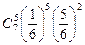 .
.
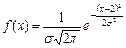 , то математическое ожидание
, то математическое ожидание 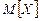 данной случайной величины равно…
данной случайной величины равно…
 ; б)
; б)  ;
в)
;
в)  ;г)
;г)  .
.
 вдоль окружности
вдоль окружности 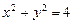 в положительном направлении.
в положительном направлении.
 найти
найти 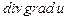 .
а)
.
а) 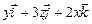 ; б)
; б) 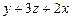 ;в)0;г) 6.
;в)0;г) 6.
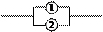
 . Работа каждого элемента является независимым событием, вероятность которого равна 0,5. Найти вероятность работы системы.
а)0,75;б)0,25;в)0,125; г)1,25.
. Работа каждого элемента является независимым событием, вероятность которого равна 0,5. Найти вероятность работы системы.
а)0,75;б)0,25;в)0,125; г)1,25.
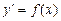
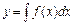 + C
+ C
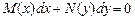


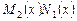 и
проинтегрировать
и
проинтегрировать 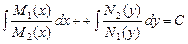
 , где
, где 

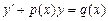
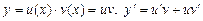
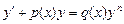
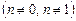

 б)
б)  в)
в) 
 б) Решается заменой
б) Решается заменой  в)Решается заменой
в)Решается заменой



 характеристичес-кого уравнения:
характеристичес-кого уравнения:  . Если
. Если


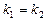

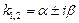 – комплексные
– комплексные


 соответству-ющего линейного однородного ДУ и одно из частных решений
соответству-ющего линейного однородного ДУ и одно из частных решений  линейного неоднородного ДУ (
линейного неоднородного ДУ ( .
.
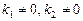
 или
или 

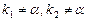
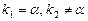 или
или 
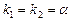
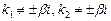

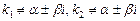


 .
.


