
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знакопостоянных числовых рядовСодержание книги
Поиск на нашем сайте
Рассмотрим числовые ряды Признак сравнения. Если для членов рядов 1) из сходимости ряда 2) из расходимости ряда Пример 10.2. Исследовать сходимость ряда
Решение. Применим признак сравнения. Так как Предельный признак сравнения. Если для членов рядов
то ряды В частности, если Например, многочлен степени
т.е. многочлен эквивалентен своей старшей степени при
При применении признаков сравнения для исследования сходимости числовых рядов удобно сравнивать с обобщенным гармоническим рядом Пример 10.3. Исследовать сходимость ряда Решение. Применим признак сравнения. Так как Здесь можно применить и предельный признак сравнения. Поскольку Пример 10.4. Исследовать сходимость ряда Решение. Попробуем применить признак сравнения: Применим предельный признак сравнения:
Ряд Пример 10.5. Исследовать сходимость ряда
Решение. Применим предельный признак сравнения:
Ряд Признак Д’Аламбера. Пусть для ряда 1) при 2) при 3) при Пример 10.6. Исследовать сходимость ряда
Решение. Применим признак Д’Аламбера. Запишем
Вычислим предел
Так как Пример 10.7. Исследовать сходимость ряда
( Решение. Применим признак Д’Аламбера. Запишем
Вычислим предел
Поскольку Радикальный признак Коши. Пусть для ряда 1) при 2) при 3) при Пример 10.8. Исследовать сходимость ряда Решение. Так как
то данный ряд расходитсяпо радикальному признаку Коши. Интегральный признак Коши. Если функция Пример 10.9. Исследовать сходимость обобщенного гармонического ряда
Решение. 1) Если Так как нарушается необходимое условие сходимости ряда, то в этом случае ряд расходится. 2) Пусть Обозначим Если
то есть несобственный интеграл расходится. Если
Следовательно, обобщенный гармонический ряд Знакочередующиеся ряды Определение. Числовой ряд Рассмотрим ряд Теорема. Если сходится ряд В этой теореме сформулирован достаточный признак сходимости ряда Определение. Если сходится ряд Определение. Знакочередующимся называется ряд, все члены которого поочередно меняют знак:
где При исследовании сходимости знакочередующихся рядов применяют признак Лейбница. Признак Лейбница. Если члены знакочередующегося ряда 2) то ряд Следствие: Остаток Таким образом, знакочередующийся ряд Пример 10.10. Исследовать сходимость ряда Решение. Так как Пример 10.11. Исследовать на абсолютную и условную сходимость ряд Решение. Исследуем ряд на абсолютную сходимость. Рассмотрим ряд, состоящий из модулей Исследуем ряд на условную сходимость. Поскольку Степенные ряды Рассмотрим теперь бесконечную последовательность функций U1 (х), U2 (х),…, Un (х),… Выражение вида
называется функциональным рядом, а сумма первых n слагаемых
n-ной частичной суммой функционального ряда. Функция
(если предел существует и конечен) называется суммой функционального ряда. Множество всех значений x, для которых ряд сходится, называется областью сходимости функционального ряда. Например, ряд Определение. Ряд вида
где При
Поскольку заменой Степенной ряд всегда сходится в точке Для степенных рядов справедлива следующая теорема. Теорема Абеля. Если степенной ряд сходится в точке Следствие. Если в точке Из теоремы Абеля и следствия вытекает, что если степенной ряд сходится хотя бы в одной точке Определение. Неотрицательное число Если ряд сходится только в точке Для определения радиуса сходимости степенного ряда используют формулы:
Пример 10.12. Найти радиус сходимости ряда Решение. Запишем n -й и (n +1)-й коэффициенты ряда
Радиус сходимости найдем по формуле
т.е. ряд сходится в единственной точке Пример 10.13. Найти область сходимости степенного ряда
Решение. Найдем радиус сходимости степенного ряда по формуле
Как видно, ряд будет сходиться для тех значений x, для которых
Таким образом, мы нашли интервал сходимости степенного ряда:
Исследуем сходимость ряда на концах интервала сходимости. При
Полученный ряд является знакочередующимся, его общий член по абсолютному значению монотонно убывает и стремится к нулю при При
Это обобщенный гармонический ряд Таким образом, Ряды Тейлора и Маклорена Если степенной ряд
Степенной ряд вида
называется рядом Тейлора функции Если
и называется рядом Маклорена. По определению полагаем Если для произвольной бесконечно дифференцируемой функции формально составить ряд Тейлора, то он может и не совпадать с самой функцией Теорема. Если на интервале
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.175 (0.008 с.) |

 с неотрицательными членами, т. е.
с неотрицательными членами, т. е. 
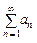 и
и  справедливо неравенство
справедливо неравенство  для
для 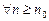 , то:
, то: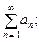
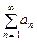 следует расходимость ряда
следует расходимость ряда 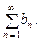
 .
.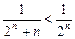 для
для  , а ряд
, а ряд  сходится как сумма бесконечно убывающей геометрической прогрессии со знаменателем
сходится как сумма бесконечно убывающей геометрической прогрессии со знаменателем  , то сходится и заданный ряд.
, то сходится и заданный ряд.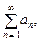
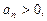 и
и 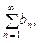
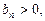 существует предел
существует предел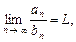
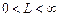 ,
, и
и 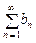 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.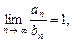 то удобно воспользоваться знаком эквивалентности и писать
то удобно воспользоваться знаком эквивалентности и писать 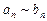 при
при 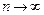 .
.

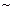
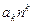 ,
,
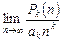
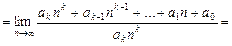
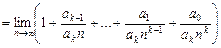
 .
.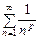 , который сходится при
, который сходится при 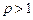 и расходится при
и расходится при  . При
. При 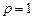 получаем гармонический ряд
получаем гармонический ряд 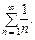
 .
. 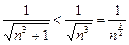 , а ряд
, а ряд 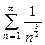 как обобщенный гармонический с показателем
как обобщенный гармонический с показателем 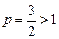 сходится, то исходный ряд также сходится.
сходится, то исходный ряд также сходится.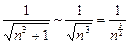 при
при  .
. 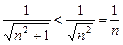 . Но ряд
. Но ряд  является гармоническим и расходится. Поэтому признак сравнения в данном случае не решает вопрос о сходимости ряда.
является гармоническим и расходится. Поэтому признак сравнения в данном случае не решает вопрос о сходимости ряда.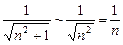 при
при  .
. 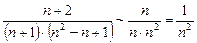 при
при 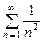 сходится как обобщенный гармонический ряд с показателем
сходится как обобщенный гармонический ряд с показателем 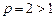 . Следовательно, исходный ряд также сходится.
. Следовательно, исходный ряд также сходится.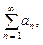
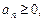 существует предел
существует предел 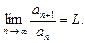 Тогда:
Тогда: ряд
ряд 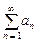 сходится;
сходится; ряд
ряд  признак Д’Аламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуют с помощью других признаков.
признак Д’Аламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуют с помощью других признаков.
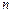 -ый и
-ый и 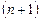 -ый члены ряда:
-ый члены ряда: ,
, 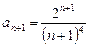 .
.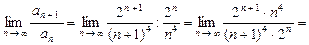

 , то данный ряд расходится.
, то данный ряд расходится.
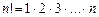 и называется «эн-факториал»).
и называется «эн-факториал»). ,
, 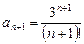 .
.
 .
.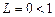 , то данный ряд сходится.
, то данный ряд сходится.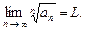 Тогда:
Тогда: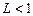 ряд
ряд  сходится;
сходится; ряд
ряд 
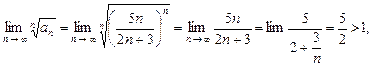
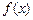 на промежутке
на промежутке  монотонно убывает и неотрицательна, то ряд
монотонно убывает и неотрицательна, то ряд 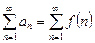 и несобственный интеграл
и несобственный интеграл 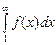 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.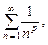

 .
.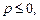 то
то 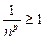 для
для 
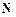 , а
, а 
 .
.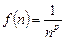 и рассмотрим функцию
и рассмотрим функцию 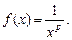 Функция
Функция 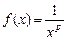 монотонно убывает и положительна на промежутке
монотонно убывает и положительна на промежутке 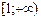 . Вычислим несобственный интеграл
. Вычислим несобственный интеграл  .
.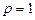 , то
, то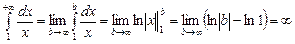 ,
,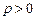 и
и  , то
, то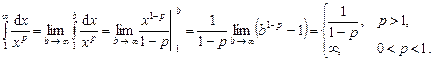
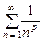 сходится при
сходится при 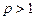 и расходится при
и расходится при 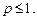
 , члены которого имеют разные знаки, называется знакопеременным.
, члены которого имеют разные знаки, называется знакопеременным. , который является знакоположительным.
, который является знакоположительным. . Обратное утверждение в общем случае неверно.
. Обратное утверждение в общем случае неверно. расходится, то ряд
расходится, то ряд 
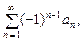 (10.1)
(10.1)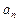 ,
,  – числа одного знака.
– числа одного знака.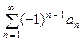 удовлетворяют условиям: 1)
удовлетворяют условиям: 1)  для
для 

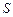 не превосходит первого члена, т.е.
не превосходит первого члена, т.е. 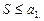
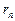 знакочередующегося ряда удовлетворяет неравенству
знакочередующегося ряда удовлетворяет неравенству 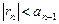 .
.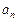 монотонно убывая стремится к нулю (
монотонно убывая стремится к нулю (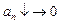 при
при 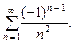
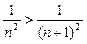 для
для 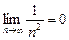 (т. е.
(т. е. 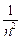 монотонно убывая стремится к нулю при
монотонно убывая стремится к нулю при 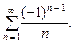
 – это расходящийся гармонический ряд.
– это расходящийся гармонический ряд. монотонно убывая стремится к нулю при
монотонно убывая стремится к нулю при 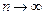 , то по признаку Лейбница ряд сходится. Следовательно, исходный ряд сходится условно.
, то по признаку Лейбница ряд сходится. Следовательно, исходный ряд сходится условно.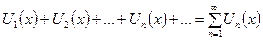
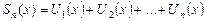
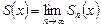
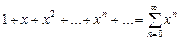 при
при 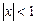 является суммой членов бесконечно убывающей геометрической прогрессии и, следовательно, сходится, причем сумма ряда
является суммой членов бесконечно убывающей геометрической прогрессии и, следовательно, сходится, причем сумма ряда 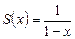 . Таким образом, областью сходимости данного функционального ряда является интервал (– 1; 1).
. Таким образом, областью сходимости данного функционального ряда является интервал (– 1; 1). (10.2)
(10.2)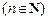 ,
, 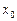 – действительные числа, называется степенным рядом по степеням
– действительные числа, называется степенным рядом по степеням  , а числа
, а числа  получаем степенной ряд по степеням
получаем степенной ряд по степеням 
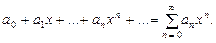
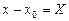 ряд (10.2) можно свести к последнему ряду, то ограничимся рассмотрением таких рядов.
ряд (10.2) можно свести к последнему ряду, то ограничимся рассмотрением таких рядов.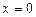 . При
. При 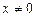 степенной ряд может как сходиться, так и расходиться.
степенной ряд может как сходиться, так и расходиться.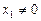 , то он сходится абсолютно для любых x таких, что
, то он сходится абсолютно для любых x таких, что 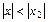 .
. степенной ряд расходится, то он расходится для любых
степенной ряд расходится, то он расходится для любых  .
.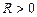 , такое, что степенной ряд сходится (абсолютно) для всех
, такое, что степенной ряд сходится (абсолютно) для всех 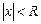 и расходится для всех
и расходится для всех 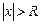 . При
. При  ряд может быть как сходящимся, так и расходящимся.
ряд может быть как сходящимся, так и расходящимся.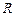 такое, что степенной ряд сходится при
такое, что степенной ряд сходится при  – интервалом сходимости степенного ряда.
– интервалом сходимости степенного ряда.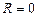 ; если же он сходится для всех действительных
; если же он сходится для всех действительных 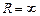 .
.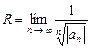 ,
,  (10.3)
(10.3) .
.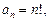

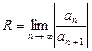
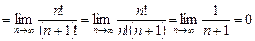 ,
,
 , где
, где  ,
, 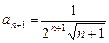

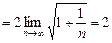
 , или
, или  , или
, или 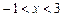 .
.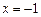 получим числовой ряд
получим числовой ряд
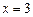 получим числовой ряд
получим числовой ряд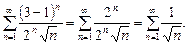
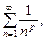 где
где 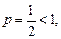 который расходится. Следовательно, значение
который расходится. Следовательно, значение 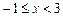 – область сходимости исследуемого ряда.
– область сходимости исследуемого ряда. сходится и его сумма
сходится и его сумма 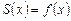 , то коэффициенты этого ряда определяются по формулам:
, то коэффициенты этого ряда определяются по формулам: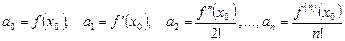 .
.
 ,
,

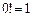 .
. .Поэтому важно определить, когда ряд Тейлора сходится к функции
.Поэтому важно определить, когда ряд Тейлора сходится к функции 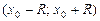 функция
функция 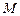 , то ее ряд Тейлора сходится к функции
, то ее ряд Тейлора сходится к функции 


