
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление двойного интеграла сводится к вычислению повторного интеграла следующим образом.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1) Пусть область
Рис. 11.2 При выборе внешнего интегрирования по переменной x (из рис.11.2 видно Тогда
Правая часть формулы называется повторным интегралом. Таким образом, вычисление двойного интеграла свелось к вычислению повторного (двух определенных интегралов) интеграла вида
При вычислении «внутреннего интеграла» (записанного в квадратных скобках) x считается постоянным. 2) Пусть область
Рис. 11.3 При выборе внешнего интегрирования по переменной y (из рис.11.3 видно, что Тогда
При вычислении «внутреннего интеграла» y считается постоянным. Из (11.1) и (11.2) следует, что
Переход от левой части равенства (11.3) к правой и наоборот называется изменением порядка интегрирования. Если область интегрирования является неправильной, то ее мож-но представить как объединение правильных областей. Тогда двой-ной интеграл равен сумме двойных интегралов по этим областям. Пример 11.1. В двойном интеграле Решение. Построим область
Например, из первого уравнения системы находим:
Рис. 11.4 Внешнее интегрирование по переменной Область интегрирования
Внешнее интегрирование по переменной Так как верхний участок границы OBA области
Пример 11.2. Вычислить двойной интеграл Решение. Построим область Найдем точки пересечения линий из системы уравнений
Таким образом,
Рис. 11.5 Область интегрирования
Если проводить внешнее интегрирование по переменной
Вычисление двойного интеграла В полярных координатах Если в двойном интеграле
Тогда
Вычисление последнего интеграла, как правило, упрощается. Пример 11.3. Вычислить Решение. Построим область Так область Запишем уравнение окружности в полярных координатах:
Рис. 11.6 Длина радиус-вектора меняется от 0 до 3, при движении конца радиус-вектора вдоль полуокружности угол поворота изменяется от 0 до Таким образом, область Следовательно,
Приложения двойного интеграла к задачам Геометрии и механики 1) Площадь плоской фигуры, занимающей область
2) Объем
Рис. 11.7 3) Площадь поверхности
4) Масса пластинки с поверхностной плотностью
5) Статические моменты относительно осей
5) Координаты центра масс плоской пластинки
где 6) С помощью двойного интеграла можно вычислить также моменты инерции плоской пластины (см. [1], гл. 14, §9). Пример 11.4. Вычислить площадь фигуры, ограниченной прямой
Рис. 11.8 Решение. Найдем точки пересечения линий:
Построим область интегрирования
Пример11.5. Найти массу плоской пластинки Решение. Построим область интегрирования (рис. 11.9). Массу пластинки найдем по формуле Область
Рис. 11.9 Следовательно,
Пример11.6. Вычислить объем тела Решение. Данное тело
Рис. 11.10 Рис. 11.11 Проекцией тела Тогда
Тройной интеграл Аналогично двойному интегралу вводится понятие тройного интеграла. Пусть функция
Предел последовательности интегральных сумм
С помощью тройного интеграла вычисляют: 1. Объем тела, занимающего область
2. Массу
а также статические моменты, моменты инерции, координаты центра масс тела ([1], гл. 14, §14). Вычисление тройного интеграла сводится к вычислению повторного интеграла([1], гл. 14, §12). Например, объем тела из примера 11.6 с помощью тройного интеграла можно вычислить следующим образом. Из рис.11.10 видно, что тело ограничено плоскостью
Далее вычисления интеграла повторяют вычисления из задачи 11.6.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 1. В двойном интеграле 2. Найти площадь фигуры, ограниченной линиями 3. Найти массу плоской пластинки 4. Найти объем тела 5. Найти массу плоской пластинки
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 892; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.009 с.) |

 является правильной в направлении оси
является правильной в направлении оси 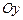 и ограничена линиями:
и ограничена линиями: 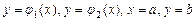 , причем
, причем 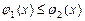 ,
,  (рис. 11.2).
(рис. 11.2).

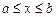 ) для определения внутренних пределов интегрирования по переменной y по области интегрирования проводим прямую, параллельную оси
) для определения внутренних пределов интегрирования по переменной y по области интегрирования проводим прямую, параллельную оси  , которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую
, которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую  , которую назовем линией выхода. То есть значение переменной
, которую назовем линией выхода. То есть значение переменной 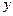 в области
в области  .
. =
=  . (11.1)
. (11.1) .
. и ограничена линиями:
и ограничена линиями:  , причем
, причем 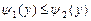 ,
,  (рис. 11.3).
(рис. 11.3).

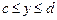 ) для определения внутренних пределов интегрирования по переменной x по области интегрирования проводим прямую, параллельную оси
) для определения внутренних пределов интегрирования по переменной x по области интегрирования проводим прямую, параллельную оси 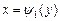 , которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую
, которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую  , которую назовем линией выхода. То есть значение переменной
, которую назовем линией выхода. То есть значение переменной  в области
в области 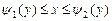 .
.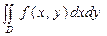 =
= 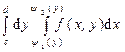 . (11.2)
. (11.2)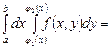
 расставить пределы интегрирования двумя способами, если область
расставить пределы интегрирования двумя способами, если область 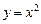 ,
,  ,
, 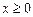 .
.
 ,
,  ,
,  ,
,
 ,
, 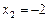 .
. ,
, 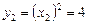 . Таким образом парабола и прямая пересекаются в двух точках с координатами
. Таким образом парабола и прямая пересекаются в двух точках с координатами  и
и  , одна из которых
, одна из которых 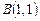 принадлежит границе области
принадлежит границе области 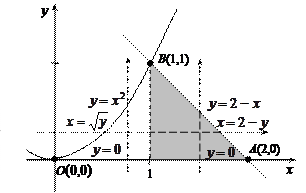

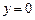 ,
, 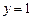 , а переменная
, а переменная 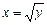 до точек прямой
до точек прямой  (рис. 11.4). Следовательно,
(рис. 11.4). Следовательно, .
. разбивает область
разбивает область 
 ,
, 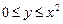 и
и 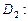
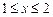 ,
,  . В результате получаем сумму двух повторных интегралов:
. В результате получаем сумму двух повторных интегралов: .
.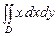 , если область
, если область 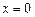 ,
,  ,
, 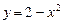 .
.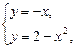
 ,
,  ,
, 
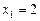 ,
, 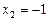 .
.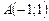 – точка пересечения линий в рассматри-ваемой области.
– точка пересечения линий в рассматри-ваемой области.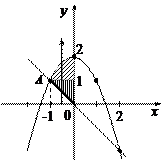

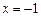 ,
, 

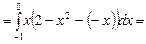
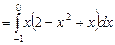




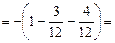
 .
.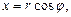
 ,
, .
. .
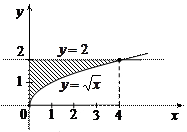
. , где область
, где область  и осью
и осью  .
.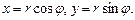

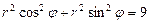

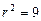
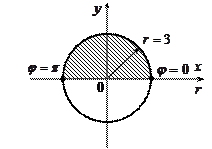
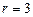 .
.

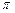 .
. , задаваемую неравенствами
, задаваемую неравенствами 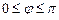 ,
,  .
.

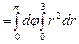

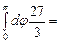

 .
.
 .
. тела, ограниченного сверху поверхностью
тела, ограниченного сверху поверхностью  , снизу – плоскостью
, снизу – плоскостью  и цилиндрической поверхностью с образующей, параллельной оси
и цилиндрической поверхностью с образующей, параллельной оси 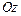 (рис.11.7), можно найти по формуле
(рис.11.7), можно найти по формуле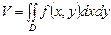 .
.

 , которая проектируется на область
, которая проектируется на область  , вычисляется по формуле
, вычисляется по формуле .
.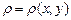 , занимающей область
, занимающей область  .
. ,
, 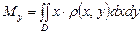 .
. , вычисляются по формулам
, вычисляются по формулам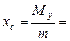
 ,
, 
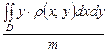
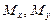 – статические моменты пластинки относительно осей
– статические моменты пластинки относительно осей  и параболой
и параболой 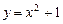 .
.

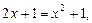
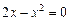 из системы уравнений
из системы уравнений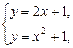



 , ограниченной линиями
, ограниченной линиями  ,
, 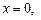
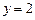 .
. .
.
 .
.







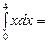

 .
.
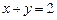 ,
, 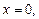
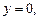

 с образующей, параллельной оси
с образующей, параллельной оси  (рис. 11.10).
(рис. 11.10).



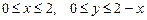 .
.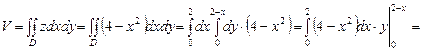
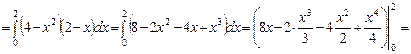
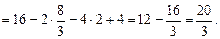
 определена (и непрерывна) в некоторой замкнутой области
определена (и непрерывна) в некоторой замкнутой области 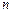 элементарных областей
элементарных областей 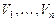 с объемами
с объемами  . Внутри каждой элементарной области
. Внутри каждой элементарной области 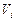 выберем произвольную точку
выберем произвольную точку  и составим сумму
и составим сумму .
. , когда наибольший из диаметров
, когда наибольший из диаметров 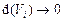 , называется тройным интегралом от функции
, называется тройным интегралом от функции  .
. .
.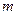 тела с переменной плотностью
тела с переменной плотностью 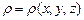
 ,
,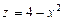 сверху и проектируется на треугольник(рис. 11.11). Поэтому область
сверху и проектируется на треугольник(рис. 11.11). Поэтому область 

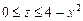 . Объем тела с помощью тройного интеграла вычисляем по формуле
. Объем тела с помощью тройного интеграла вычисляем по формуле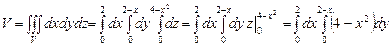 .
. ,
,  .
.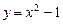 ,
,  , ограниченной линиями
, ограниченной линиями 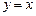 ,
, 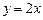 ,
,  .
.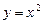 и плоскостями
и плоскостями 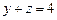 ,
,  , ограниченной линиями
, ограниченной линиями  ,
, 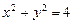 ,
,  .
.


