Раздел IX. Определенный интеграл
Оглавление
Раздел IX. Определенный интеграл. 4
Задача о площади криволинейной трапеции. 5
Формула Ньютона-Лейбница. 9
Свойства определенного интеграла. 11
Геометрический смысл определенного интеграла. 14
Замена переменной и интегрирование по частям в определенном интеграле. 19
Некоторые приложения определенного интеграла. 26
Несобственные интегралы.. 32
Раздел X. Дифференциальные уравнения. 41
Дифференциальные уравнения первого порядка. 42
Уравнения в дифференциалах. 47
Уравнение с разделенными переменными. 51
Уравнение с разделяющимися переменными. 54
Однородное уравнение. 68
Линейное уравнение. 73
Дифференциальные уравнения второго порядка. 79
Уравнения, допускающие понижение порядка. 83
Линейные дифференциальные уравнения второго порядка. 95
Линейные дифференциальные уравнения с постоянными коэффициентами. 102
Раздел IX. Определенный интеграл
Пройденный нами неопределенный интеграл применяется, в основном, как инструмент, причем в двух основных направлениях. Во-первых, он помогает вычислению так называемого определенного интеграла (к его определению мы сейчас и приступим), который и имеет разнообразнейшие практические приложения во всех областях деятельности. Во-вторых, неопределенный интеграл помогает решать так называемые дифференциальные уравнения, с которыми мы познакомимся в следующей теме.
Многие из основных понятий математики возникли из необходимости решения практических задач, возникающих в человеческой деятельности. Так, например, к понятию производной привела задача нахождения (мгновенной) скорости при неравномерном движении. Вторая производная соответствует понятию ускорения в конкретный момент времени. Понятие (определенного) интеграла родилось из традиционной задачи вычисления площадей разнообразных фигур. Средствами элементарной математики удавалось найти формулы только фигур, граница которых состоит из отрезков прямых (треугольник, прямоугольник, параллелограмм, трапеция и т.п.). Однако на практике возникала задача вычисления площади фигур с произвольными криволинейными границами. Из этой задачи и родилось понятие определенного интеграла. Мы тоже придем к необходимости такого понятия, рассмотрев задачу о вычислении площади фигуры (так называемой криволинейной трапеции), у которой одна (для начала) граница криволинейна.
Несобственные интегралы
При изучении определенного интеграла мы рассматривали только непрерывные на отрезке [ a,b ] функции, причем отрезок [ a,b ] был конечной длины (т.е. a≠−∞, b≠+∞). Непрерывные функции мы рассматривали по той причине, что, как писалось выше, для таких функций (хотя и не только для таких, но для таких − точно) существуют первообразные, а потому и неопределенный и определенный интеграл. Попробуем отойти от этих ограничений для подынтегральной функции в определенном интеграле.
Пусть подынтегральная функция имеет на отрезке [ a,b ] конечное число точек разрыва 1 рода (скачки). На рисунке в качестве примера изображен график функции  , имеющей одну точку разрыва 1 рода , имеющей одну точку разрыва 1 рода  . Для определения понятия определенного интеграла от такой функции по отрезку . Для определения понятия определенного интеграла от такой функции по отрезку  используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке  ) функции ) функции  по отрезку по отрезку  следующим образом: следующим образом:
(1)  . .
На каждом из отрезков  и и  подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции. подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции.
Пример 1. Вычислить  от функции от функции  , заданной двумя формулами (на разных участках изменения аргумента , заданной двумя формулами (на разных участках изменения аргумента  ): ):  . .
 Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций  и и  над соответствующими интервалами оси над соответствующими интервалами оси  . На интервале интегрирования . На интервале интегрирования  имеется одна точка разрыва 1 рода имеется одна точка разрыва 1 рода 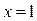 . Поэтому по определению (1): . Поэтому по определению (1):
 = { на каждом из интервалов интегрирования = { на каждом из интервалов интегрирования  и и  имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } = имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } =   Таким образом, Таким образом, 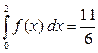 . .
Если же подынтегральная функция имеет на отрезке [ a,b ] точки разрыва 2-го рода (бесконечные скачки), то в обычном смысле определенный интеграл по этому отрезку уже не существует. Однако для некоторых из них все же можно ввести разумное понятие определенного интеграла, который будет называться несобственным интегралом 2 рода.
Если же подынтегральная функция непрерывна, но неограничен сам отрезок интегрирования (т.е.. a=−∞ и/или b=+∞), то интеграл в обычном смысле тоже не определен. Но опять же можно ввести для некоторых функций разумное понятие определенного интеграла и по бесконечному промежутку, который будет называться несобственным интегралом 1 рода. Остановимся на этом интеграле подробнее. Пусть функция  непрерывна на бесконечном интервале [ a,+∞). Можно ли разумно ввести понятие определенного интеграла по этому интервалу непрерывна на бесконечном интервале [ a,+∞). Можно ли разумно ввести понятие определенного интеграла по этому интервалу  ? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда ? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда  да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как  ). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел ). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел  . Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла . Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла  . Перейдем к точным определениям. . Перейдем к точным определениям.
Выражение вида  называется несобственным интегралом (1-го рода). Если существует конечный предел называется несобственным интегралом (1-го рода). Если существует конечный предел  , то несобственный интеграл , то несобственный интеграл  называется сходящимся, а число S называется его значением. Таким образом, можно по определению записать называется сходящимся, а число S называется его значением. Таким образом, можно по определению записать
(2)  = =  . .
Если же такой предел в правой части (2) не существует (или он равен бесконечности), то несобственный интеграл  называется расходящимся и ему не приписывается никакое числовое значение. называется расходящимся и ему не приписывается никакое числовое значение.
Таким образом, для вычисления несобственного интеграла (1-го рода)  используется следующая схема: используется следующая схема:
1) верхний предел +∞ заменить буквой b и вычислить получившийся интеграл (в ответ, конечно, будет входить буква b);
2) в ответе перейти к пределу при b→+∞.
Если предел существует, то интеграл сходится, а его значение равно значению получившегося предела. Если предел не существует, то интеграл расходится.
Пример 2. Выяснить, при каких значениях параметра  несобственный интеграл несобственный интеграл  сходится, а при каких расходится. сходится, а при каких расходится.
Решение. По изложенной выше схеме вычисляем  для произвольного значения положительного параметра для произвольного значения положительного параметра  , а затем в полученном выражении переходим к пределу при b→+∞. Поскольку неопределенный интеграл от функции , а затем в полученном выражении переходим к пределу при b→+∞. Поскольку неопределенный интеграл от функции  имеет разный вид для имеет разный вид для  и и  , то придется рассмотреть отдельно два этих случая. , то придется рассмотреть отдельно два этих случая.
1) Пусть  . Тогда . Тогда  . Поскольку . Поскольку  , то, по введенному выше определению, , то, по введенному выше определению,  при при  расходится. расходится.
2) Пусть  . Тогда . Тогда 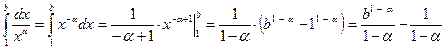 . Теперь надо в этом выражении перейти к пределу при b→+∞: . Теперь надо в этом выражении перейти к пределу при b→+∞:    {поскольку от {поскольку от  зависит только числитель в первом пределе}= зависит только числитель в первом пределе}= 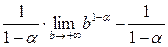 . Поэтому при . Поэтому при  : :
(3)   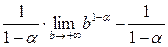 . .
Для вычисления  в (3) придется опять различать 2 случая: в (3) придется опять различать 2 случая:  и и  . .
а) Пусть  . Тогда . Тогда   . Поскольку . Поскольку  , то , то  , поэтому , поэтому  , а потому , а потому  . Поэтому при . Поэтому при  предел в (3) существует: предел в (3) существует:    . Следовательно, при . Следовательно, при  интеграл интеграл  сходится, причем его значение сходится, причем его значение  . .
б) Пусть  . Тогда в (3) . Тогда в (3)  , поскольку показатель степени , поскольку показатель степени  . Поэтому при . Поэтому при  предел в (3) равен бесконечности: предел в (3) равен бесконечности:   . Следовательно, при . Следовательно, при  интеграл интеграл  расходится. расходится.
Таким образом,  расходится при расходится при  , а при , а при  он сходится: он сходится:  . .
Точно так же с аналогичными определениями сходимости-расходимости вводится несобственный интеграл (1 рода), у которого верхний предел конечен, а нижний предел равен −∞:
(4)  = =  . .
Определим теперь несобственный интеграл от непрерывной функции по всей числовой прямой (−∞,+∞). Поскольку вводимые несобственные интегралы должны по свойствам походить на обычные, то желательно, чтобы выполнялось свойство:  , которое можно взять в качестве определения несобственного интеграла , которое можно взять в качестве определения несобственного интеграла  . Если сходятся оба несобственных интеграла . Если сходятся оба несобственных интеграла  и и  , то несобственный интеграл , то несобственный интеграл  называется сходящимся, а его значение принимается равным сумме интегралов: называется сходящимся, а его значение принимается равным сумме интегралов:
(5)  . .
Если же хотя бы один из интегралов  или или  расходится, то интеграл расходится, то интеграл  называется расходящимся. называется расходящимся.
Пример 3. Сходится ли интеграл  ? ?
Решение. По определению (4) нужно выяснить, существует ли конечный предел  . Вычислим интеграл под знаком предела, учитывая, что . Вычислим интеграл под знаком предела, учитывая, что  : :    . Тогда . Тогда  . Поэтому . Поэтому  расходится. расходится.
Пример 4. Вычислить  . .
Решение. По формуле (4):
    ={ с учетом, что ={ с учетом, что  } }  . Таким образом, интеграл сходится и . Таким образом, интеграл сходится и  . .
Пример 5. Вычислить  . .
Решение. По формуле (5):
(6)  , ,
причем, если хотя бы один из несобственных интегралов в правой части расходится, то и сам интеграл  считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов: считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов:  . Вычисляем интеграл под знаком предела: . Вычисляем интеграл под знаком предела:  ={ на интервале интегрирования ={ на интервале интегрирования  переменная интегрирования переменная интегрирования  , а потому , а потому  можно заменить на можно заменить на  }= }=  {используем формулу {используем формулу  при при  и и  } }  . Поэтому . Поэтому   (использовали, что (использовали, что  , так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6): , так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6):  . Имеем: . Имеем:  ={ на интервале интегрирования ={ на интервале интегрирования  переменная интегрирования переменная интегрирования  , а потому , а потому  можно заменить на можно заменить на  }= }=    . Поэтому . Поэтому   . Таким образом, исходный интеграл сходится, а согласно (6): . Таким образом, исходный интеграл сходится, а согласно (6):  . .
Уравнения в дифференциалах
Иногда дифференциальные уравнения первого порядка удобно рассматривать как функциональные уравнения, содержащие не производную искомой функции  , а ее дифференциал , а ее дифференциал  и дифференциал независимой переменной и дифференциал независимой переменной  . Напомним определение дифференциала. Пусть . Напомним определение дифференциала. Пусть  − произвольное число, которое в данном контексте будет называться дифференциалом независимой переменной − произвольное число, которое в данном контексте будет называться дифференциалом независимой переменной  . Тогда дифференциалом функции . Тогда дифференциалом функции  (обозначается (обозначается  ) называется выражение вида ) называется выражение вида
(1)  . .
Из определения видно, что значение дифференциала  зависит как от числового значения независимой переменной зависит как от числового значения независимой переменной  , так и от числового значения ее дифференциала , так и от числового значения ее дифференциала  . Из выражения для дифференциала (2) следует (если обе части этого выражения поделить на . Из выражения для дифференциала (2) следует (если обе части этого выражения поделить на  ), что производная ), что производная  при произвольном значении при произвольном значении  может быть выражена отношение дифференциалов может быть выражена отношение дифференциалов  и и  при любом значении дифференциала при любом значении дифференциала  : :  . Опустив для краткости обозначение аргумента, получим . Опустив для краткости обозначение аргумента, получим
(*)  . .
Поэтому очень часто производную  обозначают отношением дифференциалов обозначают отношением дифференциалов 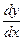 . .
Вернемся к исследуемому уравнению  . Если функция . Если функция  является его решением (на некотором интервале), то для всех является его решением (на некотором интервале), то для всех  (из этого интервала) должно выполняться тождество: (из этого интервала) должно выполняться тождество:  . Далее для краткости будем опускать упоминание о том, что . Далее для краткости будем опускать упоминание о том, что  меняется на том интервале, на котором меняется на том интервале, на котором  является решением уравнения, хотя по умолчанию это будет подразумеваться. Умножив обе части полученного равенства на произвольное число является решением уравнения, хотя по умолчанию это будет подразумеваться. Умножив обе части полученного равенства на произвольное число  (которое теперь будем рассматривать как дифференциал независимой переменной (которое теперь будем рассматривать как дифференциал независимой переменной  ), получим ), получим 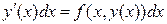 или, с учетом (1), или, с учетом (1),  . Таким образом, любое решение уравнения (1) является решением задачи для уравнения . Таким образом, любое решение уравнения (1) является решением задачи для уравнения
(2)  , ,
которая заключается в поиске такой функции  , для которой соотношение (2) выполнено для любого , для которой соотношение (2) выполнено для любого  и любого числового значения и любого числового значения  . Легко доказать и обратное, что любое решение уравнения (2) (в описанном только что смысле) является и решением уравнения (1). Поэтому можно сказать, что уравнения (1) и (2) являются разными формами записи одного и того же уравнения. Уравнение вида (2) относится к так называемым уравнениям в дифференциалах. . Легко доказать и обратное, что любое решение уравнения (2) (в описанном только что смысле) является и решением уравнения (1). Поэтому можно сказать, что уравнения (1) и (2) являются разными формами записи одного и того же уравнения. Уравнение вида (2) относится к так называемым уравнениям в дифференциалах.
Однако уравнение (2) можно значительно обобщить в следующем смысле. В уравнение (2) переменные  и и  входят не симметрично: перед дифференциалом независимой переменной входят не симметрично: перед дифференциалом независимой переменной  стоит некая произвольная функция двух переменных стоит некая произвольная функция двух переменных  и и  , а перед дифференциалом , а перед дифференциалом  нет. Исправим эту «дискриминацию», перенося к тому же обе части уравнения в одну часть. Придем к следующему уравнению: нет. Исправим эту «дискриминацию», перенося к тому же обе части уравнения в одну часть. Придем к следующему уравнению:
(3) 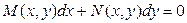 , ,
где  и и 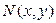 произвольные функции двух переменных. Уравнение (3) называется уравнением в дифференциалах. Что же следует называть решением такого уравнения? Прежде всего, то, что договорились называть решением уравнения вида (2): функцию произвольные функции двух переменных. Уравнение (3) называется уравнением в дифференциалах. Что же следует называть решением такого уравнения? Прежде всего, то, что договорились называть решением уравнения вида (2): функцию  , для которой соотношение (3) выполнено для любого , для которой соотношение (3) выполнено для любого  и любого числового значения и любого числового значения  . Это означает, что (вспоминая, что . Это означает, что (вспоминая, что  ) соотношение ) соотношение
(4) 
выполняется для любого  и и  . Однако симметричность вхождения . Однако симметричность вхождения  и и  в уравнение (3) позволяет расширить понятие решения этого уравнения. В уравнениях (1) и (2) переменные в уравнение (3) позволяет расширить понятие решения этого уравнения. В уравнениях (1) и (2) переменные  и и  входили несимметрично, а потому сразу было понятно, что входили несимметрично, а потому сразу было понятно, что  является аргументом, а является аргументом, а  функцией, т.е. ищется функция вида функцией, т.е. ищется функция вида  . А в уравнение (3) эти переменные входят симметрично, поэтому можно (в упоминаемом выше смысле) искать из этого уравнения как функцию . А в уравнение (3) эти переменные входят симметрично, поэтому можно (в упоминаемом выше смысле) искать из этого уравнения как функцию  , так и функцию , так и функцию  , в которой независимой переменной является , в которой независимой переменной является  , а зависимой , а зависимой  . Поэтому решением уравнения в дифференциалах (3) будем называть и такую функцию . Поэтому решением уравнения в дифференциалах (3) будем называть и такую функцию  , для которой соотношение (3) выполнено для любого , для которой соотношение (3) выполнено для любого  и любого числового значения и любого числового значения  . Это означает, что (теперь уже . Это означает, что (теперь уже 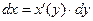 ) соотношение ) соотношение
(5) 
выполняется для любого  и и  . Таким образом, решениями уравнения в дифференциалах (3) называются как функции вида . Таким образом, решениями уравнения в дифференциалах (3) называются как функции вида  , для которых выполняется соотношение (4), так и функции вида , для которых выполняется соотношение (4), так и функции вида  , для которых выполняется соотношение (5). , для которых выполняется соотношение (5).
Поиск решений вида  и и  для уравнения (3) можно свести к решению некоторых уравнений в более привычной недифференциальной форме. Действительно, для решения уравнения (3) вида для уравнения (3) можно свести к решению некоторых уравнений в более привычной недифференциальной форме. Действительно, для решения уравнения (3) вида  должно выполняться (4), которое можно записать в виде должно выполняться (4), которое можно записать в виде  . Поскольку . Поскольку  может быть произвольным числом, то это соотношение может быть выполнено только в том случае, когда выражение в скобках перед может быть произвольным числом, то это соотношение может быть выполнено только в том случае, когда выражение в скобках перед  обращается в 0: обращается в 0:  . Перенося первое слагаемое в правую часть и деля обе части уравнения на . Перенося первое слагаемое в правую часть и деля обе части уравнения на  (см. по этому поводу замечание ниже), получаем, что функция (см. по этому поводу замечание ниже), получаем, что функция  есть решение следующего уравнения в недифференциальной форме: есть решение следующего уравнения в недифференциальной форме:
(6)  . .
Точно также, поиск решения уравнения (3) вида  приведет от соотношения (5) (при вынесении приведет от соотношения (5) (при вынесении  за скобку и последующем делении частей уравнения на за скобку и последующем делении частей уравнения на  ) к уравнению в недифференциальной форме: ) к уравнению в недифференциальной форме:
(7)  . .
Таким образом, уравнение в дифференциальной форме (3) эквивалентно совокупности двух уравнений в недифференциальной форме (6) и (7).
Замечание. При переходе от уравнения в дифференциалах (3) к уравнениям (6) и (7) нам приходилось делить обе части уравнения на 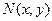 и и  , что может привести к потере некоторых решений, обращающих эти функции в ноль. Поэтому при решении конкретных уравнений при реализации этого шага следует отдельно найти решения, которые могли бы быть потеряны. , что может привести к потере некоторых решений, обращающих эти функции в ноль. Поэтому при решении конкретных уравнений при реализации этого шага следует отдельно найти решения, которые могли бы быть потеряны.
Однородное уравнение
Другим типом дифференциальных уравнений, для которых известен алгоритм получения решений, являются так называемые однородные дифференциальные уравнения 1-го порядка. Снова рассмотрим уравнения, разрешенные относительно производной, т.е. уравнения вида
(1)  . .
В предыдущем параграфе (см. формулу (6) там) мы уже выяснили, что если функция 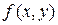 в правой части (1) может быть представлена в виде в правой части (1) может быть представлена в виде 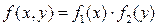 , то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций , то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций 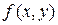 в правой части (1) известен метод решения этого уравнения? Оказывается, таковыми являются и так называемые однородные функции. в правой части (1) известен метод решения этого уравнения? Оказывается, таковыми являются и так называемые однородные функции.
Назовем функцию двух переменных 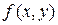 однородной функцией, если для любого значения однородной функцией, если для любого значения 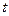 при подстановке в эту функцию при подстановке в эту функцию  вместо вместо  и и 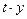 вместо вместо  выражение для функции (возможно, после некоторых тождественных преобразований) не изменяется: выражение для функции (возможно, после некоторых тождественных преобразований) не изменяется:
(2)  . .
Пример 1. Проверить однородность функции 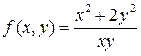 . .
Решение. Согласно (2), найдем выражение для 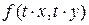 : :  {сокращаем числитель и знаменатель на {сокращаем числитель и знаменатель на 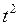 } }  . Поэтому условие (2) для . Поэтому условие (2) для 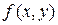 выполнено, а потому эта функция является однородной. выполнено, а потому эта функция является однородной.
Уравнение (1) называется однородным дифференциальным уравнением 1-го порядка, если функция 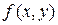 в правой его части является однородной. Оказывается, что однородные уравнения могут быть сведены к уравнению с разделяющимися переменными, алгоритм решения которых разобран в предыдущем параграфе. Делается это следующим образом: будем искать такую вспомогательную функцию в правой его части является однородной. Оказывается, что однородные уравнения могут быть сведены к уравнению с разделяющимися переменными, алгоритм решения которых разобран в предыдущем параграфе. Делается это следующим образом: будем искать такую вспомогательную функцию 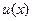 , чтобы решением уравнения (1) являлась функция , чтобы решением уравнения (1) являлась функция 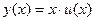 . Есть ли такие функции . Есть ли такие функции 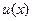 ? Оказывается, такие функции есть, а для их нахождения и получается дифференциальное уравнение с разделяющимися переменными. Как получается это уравнение – лучше разобрать на конкретных примерах. ? Оказывается, такие функции есть, а для их нахождения и получается дифференциальное уравнение с разделяющимися переменными. Как получается это уравнение – лучше разобрать на конкретных примерах.
Пример 2. Найти общее решение уравнения 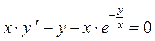 . .
Решение. Приведем это уравнение в виду (1), перенося последние два слагаемых в правую часть, а затем деля обе части уравнения на  . Получим (3) . Получим (3)
(3)  . .
Это уравнение вида (1), в котором правая часть имеет вид  . Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно, . Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно,   , а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию , а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию 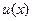 , чтобы решением уравнения (3) являлась функция , чтобы решением уравнения (3) являлась функция 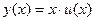 , т.е. после подстановки этой функции в уравнение (3) должно получиться верное тождество. Перед такой подстановкой найдем производную от функции , т.е. после подстановки этой функции в уравнение (3) должно получиться верное тождество. Перед такой подстановкой найдем производную от функции 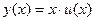 , так как в левую часть (3) именно ее и надо подставлять: , так как в левую часть (3) именно ее и надо подставлять:  ={применяем формулу для производной произведения: ={применяем формулу для производной произведения:  } }  . Теперь подставляем функцию . Теперь подставляем функцию 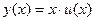 в (3), подставляя в левую часть (3) в (3), подставляя в левую часть (3)   , а в правую часть , а в правую часть  : :  или или  . Таким образом, для того, чтобы функция . Таким образом, для того, чтобы функция 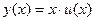 была бы решением уравнения (3), требуется, чтобы функция была бы решением уравнения (3), требуется, чтобы функция 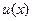 была бы решением следующего дифференциального уравнения: была бы решением следующего дифференциального уравнения:
(4)  . .
Найдем все решения этого уравнения, приведя его к уравнению с разделяющимися переменными. Сократим  в (4), а затем обе части поделим на в (4), а затем обе части поделим на  : :
(5)  . .
Это, очевидно, уравнение с разделяющимися переменными, поскольку его правая часть есть произведение двух функций, одна из которых  зависит только от независимой переменной зависит только от независимой переменной  , а другая , а другая  только от искомой функции только от искомой функции  . Решаем это уравнение по схеме, приведенной в предыдущем параграфе для решения общего уравнения с разделяющимися переменными (6): . Решаем это уравнение по схеме, приведенной в предыдущем параграфе для решения общего уравнения с разделяющимися переменными (6):
1) Умножаем обе части уравнения (5) на  , учитывая, что слева , учитывая, что слева  : получим уравнение : получим уравнение  . .
2) Делим обе части полученного уравнения на  (что равносильно умножению на (что равносильно умножению на  ), получаем уравнение с разделенными переменными ), получаем уравнение с разделенными переменными 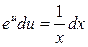 . Далее решаем по схеме решения уравнения с разделенными переменными из предыдущего параграфа. . Далее решаем по схеме решения уравнения с разделенными переменными из предыдущего параграфа.
3) «Навешиваем» интегралы на обе части уравнения:  . .
4) Вычисляем полученные интегралы (по  без « без «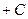 ») и приравниваем их: ») и приравниваем их:
 . Мы получили общий интеграл уравнения (выражение, связывающее . Мы получили общий интеграл уравнения (выражение, связывающее  , ,  и и  ). ).
5) Для получения из общего интеграла  общего решения (где общего решения (где  выражено через выражено через  и и  ) вычислим логарифм от правой и левой части, учитывая, что по определению логарифма ) вычислим логарифм от правой и левой части, учитывая, что по определению логарифма  . Получим общее решение уравнения (5): . Получим общее решение уравнения (5):
(6) 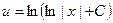 . .
Учитывая, что решения  уравнения (3) имеют вид уравнения (3) имеют вид 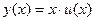 , из (6) получаем общее решение исходного уравнения: , из (6) получаем общее решение исходного уравнения:  . .
Пример 3. Решить задачу Коши  . .
Решение. Напомним, что решение этой задачи состоит в нахождении такой функции 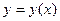 , которая, являясь одним из решений уравнения , которая, являясь одним из решений уравнения
(7)  , ,
при 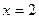 принимает значение принимает значение 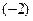 : :  . .
Проверим сначала, что уравнение (7) является однородным, для чего нужно проверить однородность функции  в правой части этого уравнения. Но такая проверка уже была проведена в примере 1. Поэтому, согласно алгоритму решения однородного уравнения, будем искать такую вспомогательную функцию в правой части этого уравнения. Но такая проверка уже была проведена в примере 1. Поэтому, согласно алгоритму решения однородного уравнения, будем искать такую вспомогательную функцию 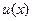 , чтобы решением уравнения (7) являлась функция , чтобы решением уравнения (7) являлась функция 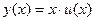 , т.е. после подстановки этой функции в уравнение (7) получилось бы верное тождество. Теперь подставляем функцию , т.е. после подстановки этой функции в уравнение (7) получилось бы верное тождество. Теперь подставляем функцию 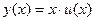 в (7), подставляя в левую часть (7) в (7), подставляя в левую часть (7)   (эта формула была легко получена в предыдущем примере), а в правую часть (эта формула была легко получена в предыдущем примере), а в правую часть  : :    . Итак, . Итак, 
| Поделиться:
| | 


 , имеющей одну точку разрыва 1 рода
, имеющей одну точку разрыва 1 рода  . Для определения понятия определенного интеграла от такой функции по отрезку
. Для определения понятия определенного интеграла от такой функции по отрезку  используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке
используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке  по отрезку
по отрезку  .
. и
и  подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции.
подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции. от функции
от функции  ):
):  .
. Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций
Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций  и
и  над соответствующими интервалами оси
над соответствующими интервалами оси  имеется одна точка разрыва 1 рода
имеется одна точка разрыва 1 рода 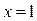 . Поэтому по определению (1):
. Поэтому по определению (1): = { на каждом из интервалов интегрирования
= { на каждом из интервалов интегрирования  и
и  имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } =
имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } = 
 Таким образом,
Таким образом, 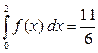 .
. ? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда
? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда  да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как
да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как  ). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел
). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел  . Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла
. Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла  . Перейдем к точным определениям.
. Перейдем к точным определениям. , то несобственный интеграл
, то несобственный интеграл  =
=  .
. несобственный интеграл
несобственный интеграл  сходится, а при каких расходится.
сходится, а при каких расходится. для произвольного значения положительного параметра
для произвольного значения положительного параметра  , а затем в полученном выражении переходим к пределу при b→+∞. Поскольку неопределенный интеграл от функции
, а затем в полученном выражении переходим к пределу при b→+∞. Поскольку неопределенный интеграл от функции  имеет разный вид для
имеет разный вид для  и
и  , то придется рассмотреть отдельно два этих случая.
, то придется рассмотреть отдельно два этих случая. . Поскольку
. Поскольку  , то, по введенному выше определению,
, то, по введенному выше определению, 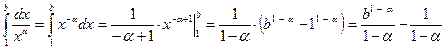 . Теперь надо в этом выражении перейти к пределу при b→+∞:
. Теперь надо в этом выражении перейти к пределу при b→+∞: 

 {поскольку от
{поскольку от 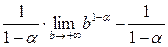 . Поэтому при
. Поэтому при 

 в (3) придется опять различать 2 случая:
в (3) придется опять различать 2 случая:  и
и  .
.
 . Поскольку
. Поскольку  , поэтому
, поэтому  , а потому
, а потому  . Поэтому при
. Поэтому при  . Следовательно, при
. Следовательно, при  сходится, причем его значение
сходится, причем его значение  .
. , поскольку показатель степени
, поскольку показатель степени  . Поэтому при
. Поэтому при  . Следовательно, при
. Следовательно, при  расходится.
расходится. , а при
, а при  =
=  .
. , которое можно взять в качестве определения несобственного интеграла
, которое можно взять в качестве определения несобственного интеграла  . Если сходятся оба несобственных интеграла
. Если сходятся оба несобственных интеграла  и
и  , то несобственный интеграл
, то несобственный интеграл  ?
? . Вычислим интеграл под знаком предела, учитывая, что
. Вычислим интеграл под знаком предела, учитывая, что  :
: 

 . Тогда
. Тогда  . Поэтому
. Поэтому  .
.


 ={ с учетом, что
={ с учетом, что  }
}  . Таким образом, интеграл сходится и
. Таким образом, интеграл сходится и  .
. .
. ,
, считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов:
считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов:  . Вычисляем интеграл под знаком предела:
. Вычисляем интеграл под знаком предела:  ={ на интервале интегрирования
={ на интервале интегрирования  переменная интегрирования
переменная интегрирования  , а потому
, а потому  можно заменить на
можно заменить на  }=
}=  {используем формулу
{используем формулу  при
при  и
и  }
}  . Поэтому
. Поэтому 
 (использовали, что
(использовали, что  , так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6):
, так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6):  . Имеем:
. Имеем:  ={ на интервале интегрирования
={ на интервале интегрирования  переменная интегрирования
переменная интегрирования  , а потому
, а потому  }=
}= 

 . Поэтому
. Поэтому 
 . Таким образом, исходный интеграл сходится, а согласно (6):
. Таким образом, исходный интеграл сходится, а согласно (6):  .
. , а ее дифференциал
, а ее дифференциал  и дифференциал независимой переменной
и дифференциал независимой переменной  . Напомним определение дифференциала. Пусть
. Напомним определение дифференциала. Пусть  (обозначается
(обозначается  .
. при произвольном значении
при произвольном значении  . Опустив для краткости обозначение аргумента, получим
. Опустив для краткости обозначение аргумента, получим .
. обозначают отношением дифференциалов
обозначают отношением дифференциалов 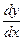 .
. . Если функция
. Если функция  . Далее для краткости будем опускать упоминание о том, что
. Далее для краткости будем опускать упоминание о том, что 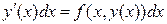 или, с учетом (1),
или, с учетом (1),  . Таким образом, любое решение уравнения (1) является решением задачи для уравнения
. Таким образом, любое решение уравнения (1) является решением задачи для уравнения ,
, входят не симметрично: перед дифференциалом независимой переменной
входят не симметрично: перед дифференциалом независимой переменной 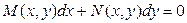 ,
, и
и 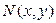 произвольные функции двух переменных. Уравнение (3) называется уравнением в дифференциалах. Что же следует называть решением такого уравнения? Прежде всего, то, что договорились называть решением уравнения вида (2): функцию
произвольные функции двух переменных. Уравнение (3) называется уравнением в дифференциалах. Что же следует называть решением такого уравнения? Прежде всего, то, что договорились называть решением уравнения вида (2): функцию  ) соотношение
) соотношение
 , в которой независимой переменной является
, в которой независимой переменной является 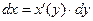 ) соотношение
) соотношение
 . Поскольку
. Поскольку  . Перенося первое слагаемое в правую часть и деля обе части уравнения на
. Перенося первое слагаемое в правую часть и деля обе части уравнения на  (см. по этому поводу замечание ниже), получаем, что функция
(см. по этому поводу замечание ниже), получаем, что функция  .
. ) к уравнению в недифференциальной форме:
) к уравнению в недифференциальной форме: .
.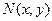 и
и  , что может привести к потере некоторых решений, обращающих эти функции в ноль. Поэтому при решении конкретных уравнений при реализации этого шага следует отдельно найти решения, которые могли бы быть потеряны.
, что может привести к потере некоторых решений, обращающих эти функции в ноль. Поэтому при решении конкретных уравнений при реализации этого шага следует отдельно найти решения, которые могли бы быть потеряны.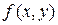 в правой части (1) может быть представлена в виде
в правой части (1) может быть представлена в виде 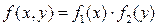 , то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций
, то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций 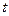 при подстановке в эту функцию
при подстановке в эту функцию  вместо
вместо 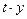 вместо
вместо  .
.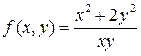 .
.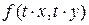 :
:  {сокращаем числитель и знаменатель на
{сокращаем числитель и знаменатель на 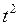 }
}  . Поэтому условие (2) для
. Поэтому условие (2) для 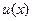 , чтобы решением уравнения (1) являлась функция
, чтобы решением уравнения (1) являлась функция 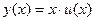 . Есть ли такие функции
. Есть ли такие функции 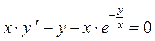 .
. .
. . Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно,
. Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно, 
 , а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию
, а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию  ={применяем формулу для производной произведения:
={применяем формулу для производной произведения:  }
}  . Теперь подставляем функцию
. Теперь подставляем функцию  , а в правую часть
, а в правую часть  :
:  или
или  . Таким образом, для того, чтобы функция
. Таким образом, для того, чтобы функция  в (4), а затем обе части поделим на
в (4), а затем обе части поделим на  .
. зависит только от независимой переменной
зависит только от независимой переменной  только от искомой функции
только от искомой функции  : получим уравнение
: получим уравнение  .
. (что равносильно умножению на
(что равносильно умножению на  ), получаем уравнение с разделенными переменными
), получаем уравнение с разделенными переменными 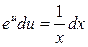 . Далее решаем по схеме решения уравнения с разделенными переменными из предыдущего параграфа.
. Далее решаем по схеме решения уравнения с разделенными переменными из предыдущего параграфа. .
.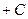 ») и приравниваем их:
») и приравниваем их: . Мы получили общий интеграл уравнения (выражение, связывающее
. Мы получили общий интеграл уравнения (выражение, связывающее  ).
). . Получим общее решение уравнения (5):
. Получим общее решение уравнения (5):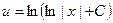 .
. уравнения (3) имеют вид
уравнения (3) имеют вид  .
. .
.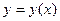 , которая, являясь одним из решений уравнения
, которая, являясь одним из решений уравнения ,
,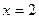 принимает значение
принимает значение 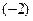 :
:  .
. в правой части этого уравнения. Но такая проверка уже была проведена в примере 1. Поэтому, согласно алгоритму решения однородного уравнения, будем искать такую вспомогательную функцию
в правой части этого уравнения. Но такая проверка уже была проведена в примере 1. Поэтому, согласно алгоритму решения однородного уравнения, будем искать такую вспомогательную функцию 

 . Итак,
. Итак, 


