Уравнение с разделяющимися переменными
В предыдущем параграфе мы установили схему решения уравнения с разделенными переменными. В данном параграфе рассмотрим некоторые типы уравнений, которые могут быть сведены к уравнениям с разделенными переменными, а потому носят название уравнений с разделяющимися переменными. Рассмотрим сначала общее уравнение 1-го порядка в дифференциальной форме 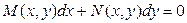 . Как будет далее понятно, такое уравнение сводится к уравнению с разделенными переменными, если функции . Как будет далее понятно, такое уравнение сводится к уравнению с разделенными переменными, если функции 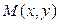 и и 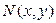 представимы в виде произведения двух функций, одна из которых зависит только от представимы в виде произведения двух функций, одна из которых зависит только от  , а другая только от , а другая только от  . Итак, уравнением с разделяющимися переменными (в дифференциальной форме) называется уравнение вида . Итак, уравнением с разделяющимися переменными (в дифференциальной форме) называется уравнение вида
(1)  . .
Как и прежде, перенесением первого слагаемого в правую часть, можно это уравнение привести к уравнению вида
(2)  , ,
которое, естественно, тоже называть уравнением с разделяющимися переменными. Для сведения уравнения вида (2) к уравнению с разделенными переменными, разделим обе его части на 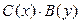 , после чего получим , после чего получим
(3)  . .
Поскольку перед 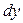 теперь оказалась функция, зависящая только от теперь оказалась функция, зависящая только от  , а перед , а перед  только от только от  , то мы и пришли к уравнению с разделенными переменными (которое, напомним, по определению должно иметь вид , то мы и пришли к уравнению с разделенными переменными (которое, напомним, по определению должно иметь вид 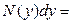 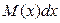 ). Далее решение проводится по схеме решения уравнения с разделенными переменными, которая описана (в рамке) в предыдущем параграфе. ). Далее решение проводится по схеме решения уравнения с разделенными переменными, которая описана (в рамке) в предыдущем параграфе.
Замечание. При сведении уравнения (2) к уравнению с разделенными переменными мы делили обе его части на 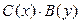 . После такого преобразования мы могли потерять те решения исходного уравнения (2), которые обращают это выражение в 0. Пусть некоторое число . После такого преобразования мы могли потерять те решения исходного уравнения (2), которые обращают это выражение в 0. Пусть некоторое число  является корнем уравнения является корнем уравнения 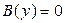 (т.е. (т.е. 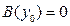 ). Докажем тогда, что функция ). Докажем тогда, что функция 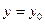 (тождественная константа) является решением исходного уравнения (2) (хотя, очевидно, не является решением полученного уравнения с разделенными переменными (3)). Подставим функцию (тождественная константа) является решением исходного уравнения (2) (хотя, очевидно, не является решением полученного уравнения с разделенными переменными (3)). Подставим функцию 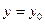 в (2), учитывая, что в (2), учитывая, что  : : 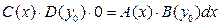 . Получили верное тождество . Получили верное тождество 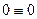 (учитывая, что (учитывая, что 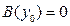 ), а потому функция ), а потому функция 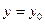 является решением уравнения (2). Точно так же, пусть некоторое число является решением уравнения (2). Точно так же, пусть некоторое число 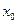 является корнем уравнения является корнем уравнения 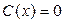 . Докажем тогда, что функция . Докажем тогда, что функция 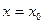 (тоже тождественная константа, но уже рассматриваемая как функция (тоже тождественная константа, но уже рассматриваемая как функция 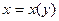 ) является решением исходного уравнения (2). Подставим функцию ) является решением исходного уравнения (2). Подставим функцию 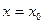 в (2), учитывая, что в (2), учитывая, что  : : 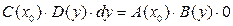 . Получили верное тождество . Получили верное тождество 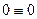 (учитывая, что (учитывая, что 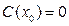 ), а потому функция ), а потому функция 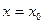 является решением уравнения (2). является решением уравнения (2).
Из этого замечания выведем следующее
Следствие. Пусть числа 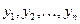 являются решениями уравнения являются решениями уравнения 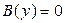 , а числа , а числа 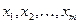 решениями решениями 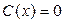 . Тогда функции . Тогда функции 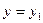 , , 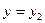 , …, , …, 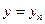 , а также функции , а также функции  , ,  , …, , …,  являются решениями уравнения (2), которые не могут быть получены из общего решения уравнения с разделенными переменными (3), а потому являются особыми решениями уравнения (2). являются решениями уравнения (2), которые не могут быть получены из общего решения уравнения с разделенными переменными (3), а потому являются особыми решениями уравнения (2).
Таким образом, определяется следующая схема решения уравнения с разделяющимися переменными (2):
1. Привести уравнение (2) к виду (3), деля обе его части на 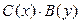 . .
2. Найти общий интеграл (а если возможно, то и общее решение) уравнения с разделенными переменными (3) по схеме, описанной (в рамке) в предыдущем параграфе.
3. Найти корни 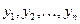 уравнения уравнения 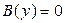 (если они есть) и корни (если они есть) и корни 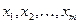 уравнения уравнения 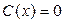 (если они тоже есть). (если они тоже есть).
4. Совокупность всех решений уравнения (2) состоит из решений, содержащихся в общем интеграле (или общем решении), полученном во втором пункте, к которым добавляются решения вида 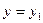 , , 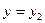 , …, , …, 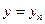 и и  , ,  , …, , …,  (особые решения уравнения). (особые решения уравнения).
Пример 1. Решить уравнение 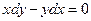 и построить его интегральные кривые. и построить его интегральные кривые.
Решение. Это уравнение с разделяющимися переменными вида (1). Перенося второе слагаемое в правую часть, приводим его к виду (2): 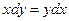 . Далее решаем это уравнение по приведенной выше схеме. . Далее решаем это уравнение по приведенной выше схеме.
1. Делим обе части на  , получаем уравнение с разделенными переменными , получаем уравнение с разделенными переменными
(4) 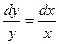 . .
2. Находим общий интеграл уравнения (4) по схеме решения уравнений с разделенными переменными из предыдущего параграфа:
1) «Навешиваем» интегралы на обе части уравнения:  . .
2) Вычисляем полученные интегралы (по  без « без «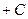 ») и приравниваем их: ») и приравниваем их:
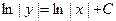 . Мы получили общий интеграл уравнения (выражение, связывающее . Мы получили общий интеграл уравнения (выражение, связывающее  , ,  и и  ). ).
3) Для получения из общего интеграла 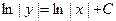 общего решения (где общего решения (где  выражено через выражено через  и и  ) используем следующий прием. Произвольная постоянная ) используем следующий прием. Произвольная постоянная  может быть любым числом, а любое число может быть представлено в виде логарифма некоторого положительного числа: может быть любым числом, а любое число может быть представлено в виде логарифма некоторого положительного числа: 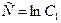 , где , где 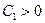 (в этом случае (в этом случае 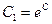 ). Поэтому общий интеграл можно записать в виде ). Поэтому общий интеграл можно записать в виде 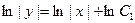 , где , где  − любое положительное число. Учитывая свойства логарифмов, получаем − любое положительное число. Учитывая свойства логарифмов, получаем 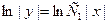 или или  . Отсюда . Отсюда  или или 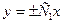 . Поскольку . Поскольку  может принимать любое строго положительное значение, то может принимать любое строго положительное значение, то 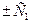 пробегает все числовые значения, кроме нуля. Вводя снова обозначение без индексов пробегает все числовые значения, кроме нуля. Вводя снова обозначение без индексов 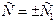 , получаем общее решение уравнения , получаем общее решение уравнения 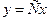 , где , где  − любое число, кроме − любое число, кроме  : : 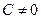 . .
3. Ищем особые решения уравнения. При приведении уравнения к уравнению с разделенными переменными, мы делили уравнение на  . Корнями уравнения . Корнями уравнения  и и  являются, очевидно, числа являются, очевидно, числа  и и  . .
4. Таким образом, общее решение уравнения 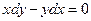 имеет вид имеет вид 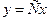 ( (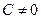 ), а два его особых решения ), а два его особых решения  и и  . Видно, что при . Видно, что при  общее решение дает одно из особых решений общее решение дает одно из особых решений  . Поэтому решениями уравнения . Поэтому решениями уравнения 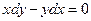 будут все функции вида будут все функции вида 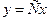 ( ( − любое число) и функция − любое число) и функция  . .
Построим интегральные кривые этого уравнения. Напомним, что таковыми являются графики решений уравнения. Поскольку графиками функций 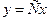 являются все прямые, проходящие через начало координат, но не совпадающие с осью являются все прямые, проходящие через начало координат, но не совпадающие с осью  , а график функции , а график функции  как раз и есть прямая, совпадающая с осью как раз и есть прямая, совпадающая с осью  , ,  то интегральными кривыми уравнения то интегральными кривыми уравнения 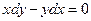 являются всевозможные прямые, проходящие через начало координат. Некоторые из них изображены на рисунке. являются всевозможные прямые, проходящие через начало координат. Некоторые из них изображены на рисунке.
Пример 2. Решить уравнение 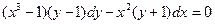 . .
Решение. Перенося второе слагаемое в правую часть, приводим его к виду (2):  . Далее решаем это уравнение по приведенной выше схеме. . Далее решаем это уравнение по приведенной выше схеме.
1. Делим обе части на 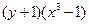 , получаем уравнение с разделенными переменными вида (2): , получаем уравнение с разделенными переменными вида (2):
(5)  . .
2. Находим общий интеграл уравнения (5) по схеме решения уравнений с разделенными переменными из предыдущего параграфа:
1) «Навешиваем» интегралы на обе части уравнения: 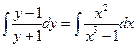 . .
2) Вычисляем отдельно полученные интегралы (по  без « без «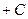 ») и приравниваем полученные выражения: ») и приравниваем полученные выражения: 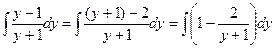 = = 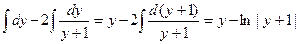 ; ; 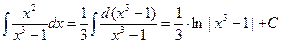 . Приравнивая полученные выражения, получим общий интеграл уравнения (выражение, связывающее . Приравнивая полученные выражения, получим общий интеграл уравнения (выражение, связывающее  , ,  и и  ): ):   . Поскольку из этого равенства мы не сможем выразить явно . Поскольку из этого равенства мы не сможем выразить явно  через через  и и  (поверьте на слово!), то общего решения уравнения мы не получим и придется довольствоваться его общим интегралом. (поверьте на слово!), то общего решения уравнения мы не получим и придется довольствоваться его общим интегралом.
3. Ищем особые решения уравнения. При приведении уравнения к уравнению с разделенными переменными, мы делили уравнение на 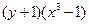 . Корнями уравнения . Корнями уравнения 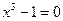 и и 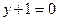 являются, очевидно, числа являются, очевидно, числа  и и  . .
4. Таким образом, общий интеграл уравнения 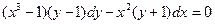 имеет вид имеет вид   , а два его особых решения , а два его особых решения  и и  . .
Рассмотрим теперь уравнения 1-го порядка в недифференциальной форме  и выясним, в каком случае его можно свести к уравнения с разделенными переменными. Оказывается, это можно сделать в том случае, если функция и выясним, в каком случае его можно свести к уравнения с разделенными переменными. Оказывается, это можно сделать в том случае, если функция 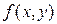 в правой части представима в виде произведения двух функций, одна из которых может зависеть только от в правой части представима в виде произведения двух функций, одна из которых может зависеть только от  , а вторая – только от , а вторая – только от  . Итак, уравнением (в недифференциальной форме) с разделяющимися переменными называется уравнение вида . Итак, уравнением (в недифференциальной форме) с разделяющимися переменными называется уравнение вида
(6)  . .
Для сведения этого уравнения к уравнению с разделенными переменными и его решения используется следующая схема.
1. Умножаем обе части уравнения (6) на  , учитывая, что слева , учитывая, что слева  . Получим уравнение . Получим уравнение 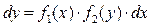 . .
2. Делим обе части полученного уравнения на  , получаем уравнение , получаем уравнение
(7)  . .
Уравнение (7) – уже уравнение с разделенными переменными, поскольку при  стоит функция, не содержащая стоит функция, не содержащая  , а при , а при  − функция, не содержащая − функция, не содержащая  . .
3. Решаем уравнение с разделенными переменными (7) по использовавшейся уже схеме из предыдущего параграфа (схема в рамке), в результате чего получаем общий интеграл (а если повезет, то из него и общее решение) уравнения (7).
4. Поскольку в пункте 2 мы делили обе части уравнения на  , то к полученному в предыдущем пункте решению нужно добавить особые решения вида , то к полученному в предыдущем пункте решению нужно добавить особые решения вида 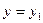 , , 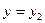 , …, , …, 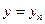 , где , где 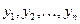 − корни уравнения − корни уравнения 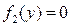 (если они, конечно, есть). (если они, конечно, есть).
Прежде, чем рассмотреть примеры применения описанной схемы, опишем некоторые приемы, которые в некоторых случаях помогают получить общее решение из общего интеграла (поскольку общее решение все же предпочтительнее общего интеграла).
Лемма. Справедливы следующие утверждения.
1. Если в общий интеграл произвольная постоянная входит с некоторым числовым множителем, то этот множитель можно отбросить (вместо 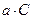 можно написать просто можно написать просто  ). ).
2. Вместо произвольной постоянной  в общем интеграле можно писать в общем интеграле можно писать 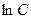 , накладывая при этом условие , накладывая при этом условие 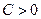 . .
3. Общий интеграл вида  (где (где 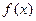 − произвольная функция) дает общее решение − произвольная функция) дает общее решение  ,где ,где  − произвольная постоянная, не равная 0 ( − произвольная постоянная, не равная 0 (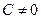 ). ).
Первые два утверждения леммы уже использовались при решении примера 1 выше, где были даны и соответствующие обоснования. Третье утверждение тоже доказывается несложно.
Пример 3. Решить уравнение 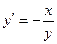 . .
Решение. Записывая уравнение в виде
(8) 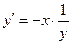 , ,
убеждаемся, что это уравнение с разделяющимися переменными вида (6), где 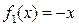 , а , а 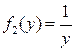 . Поэтому далее действуем по приведенной выше схеме. . Поэтому далее действуем по приведенной выше схеме.
1. Умножаем обе части (8) на  : : 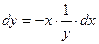 . .
2. Делим обе части на 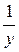 (так как (так как 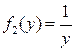 ), что равносильно умножение обеих частей на ), что равносильно умножение обеих частей на  . В результате получаем уравнение с разделенными переменными . В результате получаем уравнение с разделенными переменными 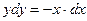 . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 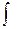 перед правой и левой частью уравнения: перед правой и левой частью уравнения:  или или 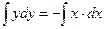 . .
2) Вычисляя полученные табличные интегралы, получаем общий интеграл уравнения 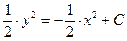 . .
3) Попробуем получить из общего интеграла общее решение. Умножая на 2, получаем 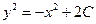 или, пользуясь первым утверждением леммы, или, пользуясь первым утверждением леммы, 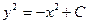 или или  . Извлекая корень, получаем два семейства общих решений: . Извлекая корень, получаем два семейства общих решений: 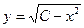 и и  . .
4. Поскольку выражение 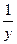 , на которые мы делили исходное уравнение, не обращается в 0 ни при каком значении , на которые мы делили исходное уравнение, не обращается в 0 ни при каком значении  , то особых решений у уравнения нет. , то особых решений у уравнения нет.
Итак, уравнение 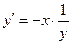 имеет 2 семейства общих решений имеет 2 семейства общих решений 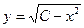 и и  . Из вида полученных общих решений видно, что они дают решения только для . Из вида полученных общих решений видно, что они дают решения только для  , а при каждом таком , а при каждом таком  решения имеют область определения решения имеют область определения  . .
Пример 4. Решить уравнение 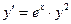 . .
Решение. Это уравнение с разделяющимися переменными вида (6), где 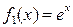 , а , а  . Поэтому далее действуем по привычной схеме. . Поэтому далее действуем по привычной схеме.
1. Умножаем обе части на  : : 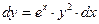 . .
2. Делим обе части на  . В результате получаем уравнение с разделенными переменными . В результате получаем уравнение с разделенными переменными  . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 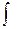 : : 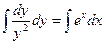 или (для удобства последующего вычисления интеграла) или (для удобства последующего вычисления интеграла)  . .
2) Вычисляя полученные табличные интегралы, получаем общий интеграл уравнения  . .
3) Выражая отсюда  , получаем общее решение , получаем общее решение 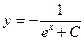 . .
4. Поскольку мы делили обе части уравнения на  , то для получения особых решений решаем уравнение , то для получения особых решений решаем уравнение 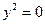 , имеющее число 0 своим единственным корнем. Особое решение: , имеющее число 0 своим единственным корнем. Особое решение:  . .
Итак, уравнение 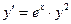 имеет общее решение имеет общее решение 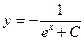 и особое решение и особое решение  . .
Пример 5. Решить уравнение 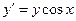 . .
Решение. Это уравнение с разделяющимися переменными вида (6), где 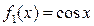 , а , а 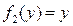 . .
1. Умножаем обе части на  : : 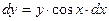 . .
2. Делим обе части на  . Получаем уравнение с разделенными переменными . Получаем уравнение с разделенными переменными 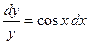 . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 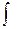 : : 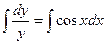 . .
2) Вычисляя полученные табличные интегралы, получаем общий интеграл уравнения 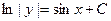 . .
3) Для получения из общего интеграла общего решения воспользуемся третьим утверждением вышеприведенной леммы: общий интеграл вида  дает общее решение дает общее решение  , где , где 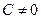 . В нашем примере . В нашем примере 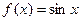 , а потому общее решение имеет вид , а потому общее решение имеет вид 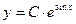 , причем , причем 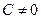 . .
4. Поскольку мы делили обе части уравнения на  , то для получения особых решений решаем уравнение , то для получения особых решений решаем уравнение  , имеющее число 0 своим единственным решением. Особое решение: , имеющее число 0 своим единственным решением. Особое решение:  . .
Заметим, что оно получается из общего решения 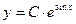 (в котором (в котором  исключалось) как раз при исключалось) как раз при  . Поэтому все решения исходного уравнения содержатся в формуле . Поэтому все решения исходного уравнения содержатся в формуле 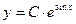 , где произвольная постоянная , где произвольная постоянная  может принимать теперь уже любые значения. может принимать теперь уже любые значения.
Пример 6. Решить уравнение  . .
Решение. Представим уравнение в виде 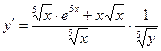 Это уравнение с разделяющимися переменными вида (6), где Это уравнение с разделяющимися переменными вида (6), где 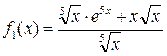 , а , а 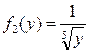 . .
1. Умножаем обе части на  : :  . .
2. Делим обе части на 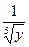 (т.е. умножаем на (т.е. умножаем на 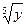 ). Получаем уравнение с разделенными переменными ). Получаем уравнение с разделенными переменными 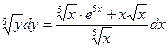 . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 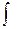 : : 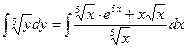 . .
2) Основная трудность этого примера – вычисление полученных интегралов. Интеграл в левой части (без «+  ): ): 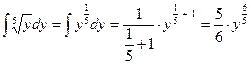 . Интеграл в правой части (с учетом, что . Интеграл в правой части (с учетом, что 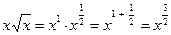 ): ): 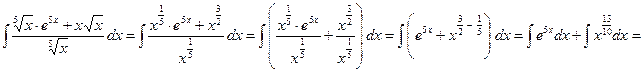  . Приравнивая полученные интегралы, получаем общий интеграл уравнения: . Приравнивая полученные интегралы, получаем общий интеграл уравнения:   . .
3) Получим из него общее решение. Сначала («расчищая» слева путь к  ) делим обе части равенства на ) делим обе части равенства на  (т.е. умножаем обе части на (т.е. умножаем обе части на 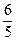 ): ):
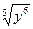  . По первому утверждению леммы . По первому утверждению леммы 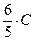 можно заменить на можно заменить на  , далее (опять «расчищая» слева путь к , далее (опять «расчищая» слева путь к  ) возводим обе части равенства в степень 5: ) возводим обе части равенства в степень 5: 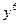 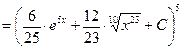 . Наконец, извлекая корень 6 степени из каждой части, получаем 2 семейства общих решений: . Наконец, извлекая корень 6 степени из каждой части, получаем 2 семейства общих решений: 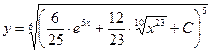 и и 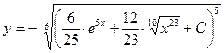 . .
4. Поскольку мы делили обе части уравнения на 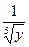 , а уравнение , а уравнение 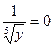 корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений: корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений: 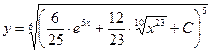 и и 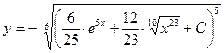 . .
Пример 7. Решить задачу Коши 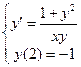 . .
Решение. Напомним, что решение этой задачи состоит в нахождении такой функции 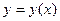 , которая, являясь одним из решений уравнения , которая, являясь одним из решений уравнения 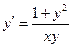 , при , при 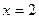 принимает значение принимает значение 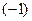 : : 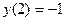 . .
Найдем сначала все решения этого уравнения, а затем выделим из них требуемое. Представим уравнение в виде 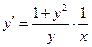 Это уравнение с разделяющимися переменными вида (6), где Это уравнение с разделяющимися переменными вида (6), где 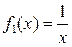 , а , а  . .
1. Умножаем обе части на  : : 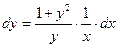 . .
2. Делим обе части на 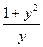 (т.е. умножаем на (т.е. умножаем на 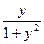 ). Получаем уравнение с разделенными переменными ). Получаем уравнение с разделенными переменными 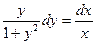 . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 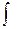 : : 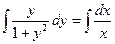 . .
2) Интеграл в левой части (без «+  ): ): 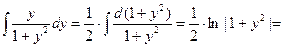 {модуль можно опустить, так как выражение под знаком модуля всегда положительно} {модуль можно опустить, так как выражение под знаком модуля всегда положительно} 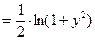 . Интеграл в правой части . Интеграл в правой части  . Приравнивая полученные интегралы, получаем общий интеграл уравнения: . Приравнивая полученные интегралы, получаем общий интеграл уравнения: 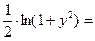 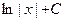 . .
3) Получим из него общее решение. Умножаем обе части на 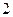 , но вместо , но вместо 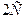 оставляем оставляем  (первое утверждение леммы): (первое утверждение леммы): 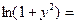 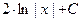 . По свойству логарифмов . По свойству логарифмов 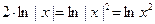 , а вместо , а вместо  запишем запишем 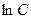 с условием с условием 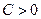 (второе утверждение леммы). Получаем (второе утверждение леммы). Получаем 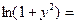 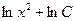 . Используя свойства логарифмов, имеем . Используя свойства логарифмов, имеем 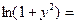 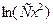 , откуда , откуда 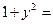 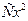 , ,  . Извлекая квадратный корень из обеих частей, получаем 2 семейства общих решений: . Извлекая квадратный корень из обеих частей, получаем 2 семейства общих решений: 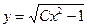 и и 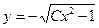 . .
4. Поскольку мы делили обе части уравнения на 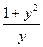 , а уравнение , а уравнение  корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений: корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений: 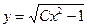 и и 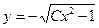 (в обоих семействах произвольная постоянная (в обоих семействах произвольная постоянная 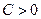 ). ).
Теперь (для решения поставленной задачи Коши), выделим из этих семейств решений ту функцию 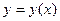 , которая при , которая при 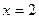 принимает значение принимает значение 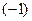 : : 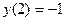 . Ясно, что при любом . Ясно, что при любом 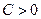 функции первого семейства не могут принимать отрицательных значений (значение квадратного корня всегда неотрицательно), а потому искомую функцию функции первого семейства не могут принимать отрицательных значений (значение квадратного корня всегда неотрицательно), а потому искомую функцию 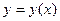 будем искать среди функций второго семейства. Какое же значение произвольной постоянной будем искать среди функций второго семейства. Какое же значение произвольной постоянной  дает во втором семействе такую функцию, которая при дает во втором семействе такую функцию, которая при 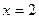 принимает значение принимает значение 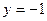 ? Подставляя ? Подставляя 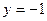 и и 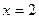 в общий вид функций этого семейства, получаем, что должно выполняться условие: в общий вид функций этого семейства, получаем, что должно выполняться условие:  . Отсюда . Отсюда 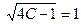 , ,  , , 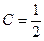 . Поэтому нужное нам решение задачи Коши получается из второго семейства общих решений . Поэтому нужное нам решение задачи Коши получается из второго семейства общих решений 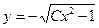 при при 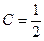 . Таким образом, решением задачи Коши является функция . Таким образом, решением задачи Коши является функция 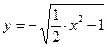 . .
Однородное уравнение
Другим типом дифференциальных уравнений, для которых известен алгоритм получения решений, являются так называемые однородные дифференциальные уравнения 1-го порядка. Снова рассмотрим уравнения, разрешенные относительно производной, т.е. уравнения вида
(1)  . .
В предыдущем параграфе (см. формулу (6) там) мы уже выяснили, что если функция 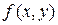 в правой части (1) может быть представлена в виде в правой части (1) может быть представлена в виде 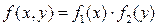 , то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций , то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций 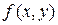 в правой части (1) известен метод решения этого уравнения? Оказывается, таковыми являются и так называемые однородные функции. в правой части (1) известен метод решения этого уравнения? Оказывается, таковыми являются и так называемые однородные функции.
Назовем функцию двух переменных 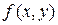 однородной функцией, если для любого значения однородной функцией, если для любого значения 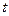 при подстановке в эту функцию при подстановке в эту функцию  вместо вместо  и и 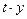 вместо вместо  выражение для функции (возможно, после некоторых тождественных преобразований) не изменяется: выражение для функции (возможно, после некоторых тождественных преобразований) не изменяется:
(2)  . .
Пример 1. Проверить однородность функции 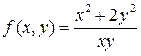 . .
Решение. Согласно (2), найдем выражение для 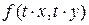 : :  {сокращаем числитель и знаменатель на {сокращаем числитель и знаменатель на 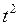 } }  . Поэтому условие (2) для . Поэтому условие (2) для 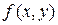 выполнено, а потому эта функция является однородной. выполнено, а потому эта функция является однородной.
Уравнение (1) называется однородным дифференциальным уравнением 1-го порядка, если функция 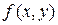 в правой его части является однородной. Оказывается, что однородные уравнения могут быть сведены к уравнению с разделяющимися переменными, алгоритм решения которых разобран в предыдущем параграфе. Делается это следующим образом: будем искать такую вспомогательную функцию в правой его части является однородной. Оказывается, что однородные уравнения могут быть сведены к уравнению с разделяющимися переменными, алгоритм решения которых разобран в предыдущем параграфе. Делается это следующим образом: будем искать такую вспомогательную функцию 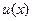 , чтобы решением уравнения (1) являлась функция , чтобы решением уравнения (1) являлась функция 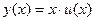 . Есть ли такие функции . Есть ли такие функции 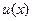 ? Оказывается, такие функции есть, а для их нахождения и получается дифференциальное уравнение с разделяющимися переменными. Как получается это уравнение – лучше разобрать на конкретных примерах. ? Оказывается, такие функции есть, а для их нахождения и получается дифференциальное уравнение с разделяющимися переменными. Как получается это уравнение – лучше разобрать на конкретных примерах.
Пример 2. Найти общее решение уравнения 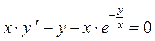 . .
Решение. Приведем это уравнение в виду (1), перенося последние два слагаемых в правую часть, а затем деля обе части уравнения на  . Получим (3) . Получим (3)
(3)  . .
Это уравнение вида (1), в котором правая часть имеет вид  . Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно, . Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно,   , а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию , а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию 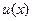 , чтобы решением уравнения (3) являлась функция , чтобы решением уравнения (3) являлась функция 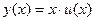 , т.е. после подстановки этой функции в уравнение (3) должно получиться верное тождество. Перед такой подстановкой найдем производную от функции , т.е. после подстановки этой функции в уравнение (3) должно получиться верное тождество. Перед такой подстановкой найдем производную от функции 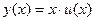 , так как в левую часть (3) именно ее и надо подставлять: , так как в левую часть (3) именно ее и надо подставлять:  ={применяем формулу для производной произведения: ={применяем формулу для производной произведения:  } }  . Теперь подставляем функцию . Теперь подставляем функцию 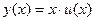 в (3), подставляя в левую часть (3) в (3), подставляя в левую часть (3)   , а в правую часть , а в правую часть  : :  | 


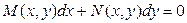 . Как будет далее понятно, такое уравнение сводится к уравнению с разделенными переменными, если функции
. Как будет далее понятно, такое уравнение сводится к уравнению с разделенными переменными, если функции 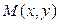 и
и 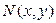 представимы в виде произведения двух функций, одна из которых зависит только от
представимы в виде произведения двух функций, одна из которых зависит только от  , а другая только от
, а другая только от  . Итак, уравнением с разделяющимися переменными (в дифференциальной форме) называется уравнение вида
. Итак, уравнением с разделяющимися переменными (в дифференциальной форме) называется уравнение вида .
. ,
,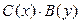 , после чего получим
, после чего получим .
.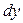 теперь оказалась функция, зависящая только от
теперь оказалась функция, зависящая только от  только от
только от 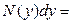
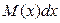 ). Далее решение проводится по схеме решения уравнения с разделенными переменными, которая описана (в рамке) в предыдущем параграфе.
). Далее решение проводится по схеме решения уравнения с разделенными переменными, которая описана (в рамке) в предыдущем параграфе. является корнем уравнения
является корнем уравнения 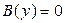 (т.е.
(т.е. 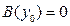 ). Докажем тогда, что функция
). Докажем тогда, что функция 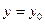 (тождественная константа) является решением исходного уравнения (2) (хотя, очевидно, не является решением полученного уравнения с разделенными переменными (3)). Подставим функцию
(тождественная константа) является решением исходного уравнения (2) (хотя, очевидно, не является решением полученного уравнения с разделенными переменными (3)). Подставим функцию  :
: 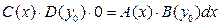 . Получили верное тождество
. Получили верное тождество 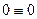 (учитывая, что
(учитывая, что 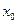 является корнем уравнения
является корнем уравнения 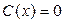 . Докажем тогда, что функция
. Докажем тогда, что функция 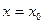 (тоже тождественная константа, но уже рассматриваемая как функция
(тоже тождественная константа, но уже рассматриваемая как функция 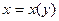 ) является решением исходного уравнения (2). Подставим функцию
) является решением исходного уравнения (2). Подставим функцию  :
: 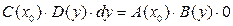 . Получили верное тождество
. Получили верное тождество 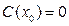 ), а потому функция
), а потому функция 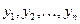 являются решениями уравнения
являются решениями уравнения 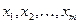 решениями
решениями 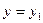 ,
, 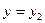 , …,
, …, 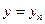 , а также функции
, а также функции  ,
,  , …,
, …,  являются решениями уравнения (2), которые не могут быть получены из общего решения уравнения с разделенными переменными (3), а потому являются особыми решениями уравнения (2).
являются решениями уравнения (2), которые не могут быть получены из общего решения уравнения с разделенными переменными (3), а потому являются особыми решениями уравнения (2).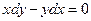 и построить его интегральные кривые.
и построить его интегральные кривые.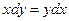 . Далее решаем это уравнение по приведенной выше схеме.
. Далее решаем это уравнение по приведенной выше схеме. , получаем уравнение с разделенными переменными
, получаем уравнение с разделенными переменными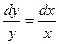 .
. .
.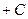 ») и приравниваем их:
») и приравниваем их: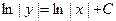 . Мы получили общий интеграл уравнения (выражение, связывающее
. Мы получили общий интеграл уравнения (выражение, связывающее  ).
).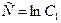 , где
, где 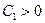 (в этом случае
(в этом случае 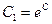 ). Поэтому общий интеграл можно записать в виде
). Поэтому общий интеграл можно записать в виде 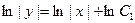 , где
, где  − любое положительное число. Учитывая свойства логарифмов, получаем
− любое положительное число. Учитывая свойства логарифмов, получаем 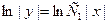 или
или  . Отсюда
. Отсюда  или
или 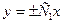 . Поскольку
. Поскольку 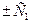 пробегает все числовые значения, кроме нуля. Вводя снова обозначение без индексов
пробегает все числовые значения, кроме нуля. Вводя снова обозначение без индексов 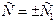 , получаем общее решение уравнения
, получаем общее решение уравнения 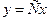 , где
, где  :
: 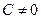 .
. и
и  являются, очевидно, числа
являются, очевидно, числа  общее решение дает одно из особых решений
общее решение дает одно из особых решений  − любое число) и функция
− любое число) и функция  то интегральными кривыми уравнения
то интегральными кривыми уравнения 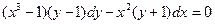 .
. . Далее решаем это уравнение по приведенной выше схеме.
. Далее решаем это уравнение по приведенной выше схеме.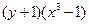 , получаем уравнение с разделенными переменными вида (2):
, получаем уравнение с разделенными переменными вида (2): .
.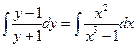 .
.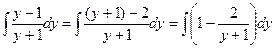 =
= 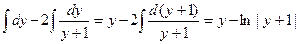 ;
; 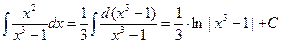 . Приравнивая полученные выражения, получим общий интеграл уравнения (выражение, связывающее
. Приравнивая полученные выражения, получим общий интеграл уравнения (выражение, связывающее 
 . Поскольку из этого равенства мы не сможем выразить явно
. Поскольку из этого равенства мы не сможем выразить явно 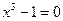 и
и 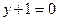 являются, очевидно, числа
являются, очевидно, числа  и
и  .
. и выясним, в каком случае его можно свести к уравнения с разделенными переменными. Оказывается, это можно сделать в том случае, если функция
и выясним, в каком случае его можно свести к уравнения с разделенными переменными. Оказывается, это можно сделать в том случае, если функция 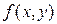 в правой части представима в виде произведения двух функций, одна из которых может зависеть только от
в правой части представима в виде произведения двух функций, одна из которых может зависеть только от  .
. . Получим уравнение
. Получим уравнение 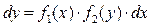 .
. , получаем уравнение
, получаем уравнение .
. стоит функция, не содержащая
стоит функция, не содержащая 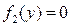 (если они, конечно, есть).
(если они, конечно, есть).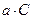 можно написать просто
можно написать просто 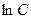 , накладывая при этом условие
, накладывая при этом условие 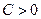 .
. (где
(где 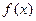 − произвольная функция) дает общее решение
− произвольная функция) дает общее решение  ,где
,где 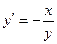 .
.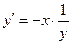 ,
,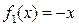 , а
, а 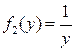 . Поэтому далее действуем по приведенной выше схеме.
. Поэтому далее действуем по приведенной выше схеме.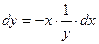 .
.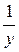 (так как
(так как 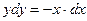 .
.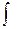 перед правой и левой частью уравнения:
перед правой и левой частью уравнения:  или
или 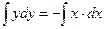 .
.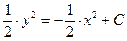 .
.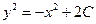 или, пользуясь первым утверждением леммы,
или, пользуясь первым утверждением леммы, 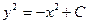 или
или  . Извлекая корень, получаем два семейства общих решений:
. Извлекая корень, получаем два семейства общих решений: 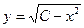 и
и  .
.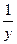 , на которые мы делили исходное уравнение, не обращается в 0 ни при каком значении
, на которые мы делили исходное уравнение, не обращается в 0 ни при каком значении  , а при каждом таком
, а при каждом таком  .
.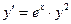 .
.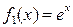 , а
, а  . Поэтому далее действуем по привычной схеме.
. Поэтому далее действуем по привычной схеме.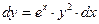 .
. . В результате получаем уравнение с разделенными переменными
. В результате получаем уравнение с разделенными переменными  .
.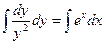 или (для удобства последующего вычисления интеграла)
или (для удобства последующего вычисления интеграла)  .
. .
.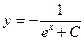 .
. , то для получения особых решений решаем уравнение
, то для получения особых решений решаем уравнение 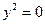 , имеющее число 0 своим единственным корнем. Особое решение:
, имеющее число 0 своим единственным корнем. Особое решение: 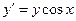 .
.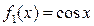 , а
, а 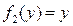 .
.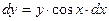 .
.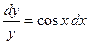 .
.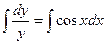 .
.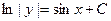 .
. дает общее решение
дает общее решение 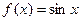 , а потому общее решение имеет вид
, а потому общее решение имеет вид 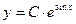 , причем
, причем  .
.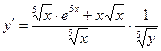 Это уравнение с разделяющимися переменными вида (6), где
Это уравнение с разделяющимися переменными вида (6), где 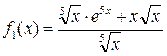 , а
, а 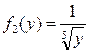 .
. .
.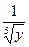 (т.е. умножаем на
(т.е. умножаем на 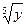 ). Получаем уравнение с разделенными переменными
). Получаем уравнение с разделенными переменными 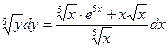 .
.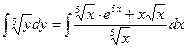 .
.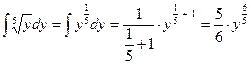 . Интеграл в правой части (с учетом, что
. Интеграл в правой части (с учетом, что 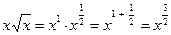 ):
): 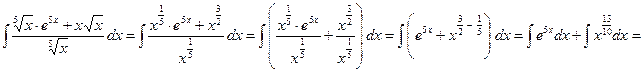
 . Приравнивая полученные интегралы, получаем общий интеграл уравнения:
. Приравнивая полученные интегралы, получаем общий интеграл уравнения: 
 .
. (т.е. умножаем обе части на
(т.е. умножаем обе части на 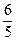 ):
):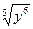
 . По первому утверждению леммы
. По первому утверждению леммы 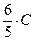 можно заменить на
можно заменить на 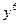
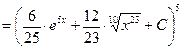 . Наконец, извлекая корень 6 степени из каждой части, получаем 2 семейства общих решений:
. Наконец, извлекая корень 6 степени из каждой части, получаем 2 семейства общих решений: 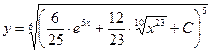 и
и 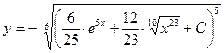 .
.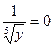 корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений:
корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений: 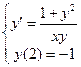 .
.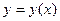 , которая, являясь одним из решений уравнения
, которая, являясь одним из решений уравнения 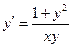 , при
, при 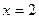 принимает значение
принимает значение 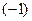 :
: 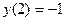 .
.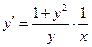 Это уравнение с разделяющимися переменными вида (6), где
Это уравнение с разделяющимися переменными вида (6), где 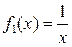 , а
, а  .
.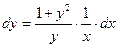 .
.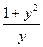 (т.е. умножаем на
(т.е. умножаем на 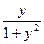 ). Получаем уравнение с разделенными переменными
). Получаем уравнение с разделенными переменными 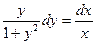 .
.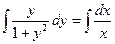 .
.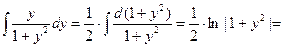 {модуль можно опустить, так как выражение под знаком модуля всегда положительно}
{модуль можно опустить, так как выражение под знаком модуля всегда положительно} 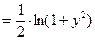 . Интеграл в правой части
. Интеграл в правой части  . Приравнивая полученные интегралы, получаем общий интеграл уравнения:
. Приравнивая полученные интегралы, получаем общий интеграл уравнения: 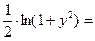
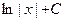 .
.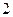 , но вместо
, но вместо 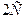 оставляем
оставляем 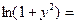
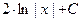 . По свойству логарифмов
. По свойству логарифмов 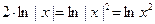 , а вместо
, а вместо 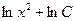 . Используя свойства логарифмов, имеем
. Используя свойства логарифмов, имеем 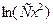 , откуда
, откуда 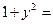
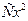 ,
,  . Извлекая квадратный корень из обеих частей, получаем 2 семейства общих решений:
. Извлекая квадратный корень из обеих частей, получаем 2 семейства общих решений: 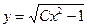 и
и 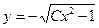 .
. корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений:
корней не имеет, то особых решений у уравнения нет. Поэтому все решения исходного уравнения содержатся в двух семействах его общих решений: 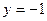 ? Подставляя
? Подставляя  . Отсюда
. Отсюда 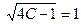 ,
,  ,
, 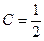 . Поэтому нужное нам решение задачи Коши получается из второго семейства общих решений
. Поэтому нужное нам решение задачи Коши получается из второго семейства общих решений 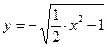 .
.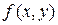 в правой части (1) может быть представлена в виде
в правой части (1) может быть представлена в виде 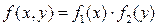 , то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций
, то уравнение (1) называется уравнением с разделяющимися переменными, для которого разобрана конкретная схема его решения. Для каких же еще типов функций 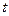 при подстановке в эту функцию
при подстановке в эту функцию  вместо
вместо 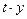 вместо
вместо  .
.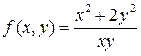 .
.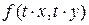 :
:  {сокращаем числитель и знаменатель на
{сокращаем числитель и знаменатель на 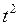 }
}  . Поэтому условие (2) для
. Поэтому условие (2) для 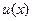 , чтобы решением уравнения (1) являлась функция
, чтобы решением уравнения (1) являлась функция 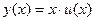 . Есть ли такие функции
. Есть ли такие функции 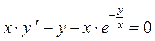 .
. .
. . Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно,
. Убедимся, что это функция является однородной, проверив выполнение соотношения (2). Действительно, 
 , а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию
, а потому уравнение (3) – однородное. Согласно приведенной выше рекомендации для этого случая, будем искать такую вспомогательную функцию  ={применяем формулу для производной произведения:
={применяем формулу для производной произведения:  }
}  . Теперь подставляем функцию
. Теперь подставляем функцию 
 , а в правую часть
, а в правую часть  :
: 


