Некоторые приложения определенного интеграла
Определенный интеграл имеет разнообразнейшие применения практически во всех областях знания. Мы уже отмечали приложения, связанные с вычислением площадей произвольных фигур с криволинейными границами. Кроме того, с помощью определенного интеграла можно вычислять длины различных кривых, объемы тел с известными площадями параллельных сечений, объемы так называемых тел вращения и площади их поверхности. Многообразны применения и в физике. К ним можно отнести вычисление длины пути по заданному закону изменения скорости, вычисление работы переменной силы на прямолинейном участке движения, вычисление статических моментов и координат центра тяжести нагруженной кривой или плоской фигуры с постоянной плотностью, определение массы неоднородного тонкого стержня по известной его меняющейся плотности, вычисление давления жидкости на вертикальную пластинку, полного заряда стержня по его (заряда) переменной плотности и так далее. К соответствующим экономическим задачам относятся задачи нахождения функций издержек, прибыли и потребления по известным соответствующим предельным функциям, нахождение объема выпуска продукции по изменяющейся производительности труда и так далее.
Остановимся подробнее на определении объема тел вращения. Пусть имеется график некоторой функции  на отрезке [ a,b ], лежащий над осью на отрезке [ a,b ], лежащий над осью  . Рассмотрим снова криволинейную трапецию, основанием которой является . Рассмотрим снова криволинейную трапецию, основанием которой является  отрезок [ a,b ], боковыми сторонами являются отрезки вертикальных прямых, проходящих через точки (числа) a и b на оси отрезок [ a,b ], боковыми сторонами являются отрезки вертикальных прямых, проходящих через точки (числа) a и b на оси  , а верхним основанием служит график этой функции. Площадь такой трапеции, как известно из изложенного выше, выражается интегралом , а верхним основанием служит график этой функции. Площадь такой трапеции, как известно из изложенного выше, выражается интегралом  , но сейчас нас площадь не интересует. Если эту криволинейную трапецию вращать вокруг оси , но сейчас нас площадь не интересует. Если эту криволинейную трапецию вращать вокруг оси  , то получится объемная фигура, которая называется телом вращения (см. рисунок). Тогда объем тела вращения можно вычислить с помощью определенного интеграла по следующей формуле: , то получится объемная фигура, которая называется телом вращения (см. рисунок). Тогда объем тела вращения можно вычислить с помощью определенного интеграла по следующей формуле:
(1)  . .
К телам вращения (из проходимых ранее в школе) относятся шары, конусы и цилиндры. Поэтому известные формулы для их объема могут быть получены из приведенной формулы (1).
Пример 1. Вывести известную из школьной программы формулу  для объема прямого кругового конуса высоты для объема прямого кругового конуса высоты 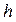 и радиуса основания и радиуса основания  . .
 Решение. Для того, чтобы воспользоваться формулой (1), представим упомянутый конус высоты Решение. Для того, чтобы воспользоваться формулой (1), представим упомянутый конус высоты 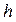 и радиуса основания и радиуса основания  как тело, полученное вращением вокруг оси как тело, полученное вращением вокруг оси  прямоугольного треугольника прямоугольного треугольника  , изображенного на рисунке. В этом треугольнике длина катета , изображенного на рисунке. В этом треугольнике длина катета  равна высоте конуса равна высоте конуса 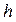 (поэтому точке (поэтому точке  на оси на оси  соответствует число соответствует число 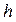 ), а длина катета ), а длина катета  равна радиусу равна радиусу  основания конуса. Теперь понятно, что в формуле (1) в качестве пределов интегрирования нужно взять основания конуса. Теперь понятно, что в формуле (1) в качестве пределов интегрирования нужно взять 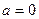 и и  . Осталось понять, какое выражение подставлять в (1) вместо . Осталось понять, какое выражение подставлять в (1) вместо 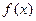 . В формуле (1) . В формуле (1) 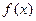 есть выражение для функции, часть графика которой, расположенная над отрезком [ a,b ], образует верхнее основание вращаемой криволинейной трапеции. Поэтому в нашем примере есть выражение для функции, часть графика которой, расположенная над отрезком [ a,b ], образует верхнее основание вращаемой криволинейной трапеции. Поэтому в нашем примере 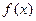 есть выражение для функции, график которой над интервалом [ 0,h ] на оси есть выражение для функции, график которой над интервалом [ 0,h ] на оси  есть отрезок прямой есть отрезок прямой  . Как известно, все наклонные прямые имеют уравнение вида . Как известно, все наклонные прямые имеют уравнение вида  . Найдем числа . Найдем числа  и и  для прямой для прямой  . Поскольку прямая проходит через начало координат . Поскольку прямая проходит через начало координат 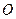 , то , то  , а потому уравнение прямой , а потому уравнение прямой  имеет вид имеет вид  . Число . Число  есть угловой коэффициент прямой есть угловой коэффициент прямой  и равен тангенсу угла и равен тангенсу угла  наклона прямой к оси наклона прямой к оси  . Этот тангенс найдем из прямоугольного треугольника . Этот тангенс найдем из прямоугольного треугольника  как отношение длины катета, противолежащего этому углу, к длине прилежащего катета. Поэтому как отношение длины катета, противолежащего этому углу, к длине прилежащего катета. Поэтому  . Итак, уравнение прямой . Итак, уравнение прямой  : :  , а потому в нашем примере в качестве , а потому в нашем примере в качестве 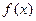 в формуле (1) должно быть взято в формуле (1) должно быть взято  . Таким образом, искомый объем конуса выражается определенным интегралом . Таким образом, искомый объем конуса выражается определенным интегралом  . Вычислим его, учитывая что высота . Вычислим его, учитывая что высота 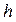 и радиус основания и радиус основания  конуса являются постоянными числами (своими для каждого конкретного конуса): конуса являются постоянными числами (своими для каждого конкретного конуса):

Что и требовалось получить.
 Пример 2. Найти объем тела, образованного вращением вокруг оси х фигуры, ограниченной графиками функций Пример 2. Найти объем тела, образованного вращением вокруг оси х фигуры, ограниченной графиками функций  и и  (см. рисунок). (см. рисунок).
Решение. В этом примере вращается не криволинейная трапеция, а более сложная фигура, поэтому напрямую формула (1) неприменима. Однако понятно, что исследуемое тело вращения может быть получено удалением из тела, образованного вращением криволинейной трапеции с верхним основанием – графиком  , тела, образованного вращением криволинейной трапеции с верхним основанием – графиком , тела, образованного вращением криволинейной трапеции с верхним основанием – графиком  . Поэтому объем искомого тела . Поэтому объем искомого тела  , где , где  и и  есть объемы описанных выше тел вращения. Второе тело вращения (полученное вращением прямоугольного треугольника) есть, очевидно, прямой круговой конус с высотой есть объемы описанных выше тел вращения. Второе тело вращения (полученное вращением прямоугольного треугольника) есть, очевидно, прямой круговой конус с высотой  и радиусом основания и радиусом основания  (см. рисунок). Поэтому его объем (см. рисунок). Поэтому его объем  можно искать не по интегральной формуле (1), а по формуле, полученной в предыдущем примере: можно искать не по интегральной формуле (1), а по формуле, полученной в предыдущем примере:  . Объем . Объем  первой фигуры вращения вычисляем с помощью интеграла по формуле (1): первой фигуры вращения вычисляем с помощью интеграла по формуле (1):  . Таким образом, искомый объем . Таким образом, искомый объем  кубических единиц. кубических единиц.
 Рассмотрим применение определенного интеграла к вычислению длины дуги кривой. Пусть дуга Рассмотрим применение определенного интеграла к вычислению длины дуги кривой. Пусть дуга  некоторой кривой является частью графика непрерывной функции некоторой кривой является частью графика непрерывной функции  при изменении при изменении 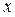 на отрезке на отрезке  (см. рисунок). Числа (см. рисунок). Числа  и и  являются абсциссами (т.е. х -координатами) начальной являются абсциссами (т.е. х -координатами) начальной  и конечной и конечной  точки дуги точки дуги  . В этом случае длина . В этом случае длина  дуги дуги  вычисляется по формуле: вычисляется по формуле:
(2)  . .
Приведем пример использования формулы (2).
Пример 3. Вычислить длину части графика функции  (так называемая полукубическая парабола), если (так называемая полукубическая парабола), если  . .
Решение. Применим формулу (2) с соответствующими этому примеру параметрами:  , ,  , , 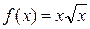 . Для удобства преобразуем выражение для функции: . Для удобства преобразуем выражение для функции:  . Тогда . Тогда  . По формуле (2) длина кривой . По формуле (2) длина кривой   {вносим {вносим  под знак дифференциала, добавляя перед интегралом поправочный множитель под знак дифференциала, добавляя перед интегралом поправочный множитель 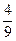 } }   . Итак, . Итак,  . .
 Рассмотрим теперь применение определенного интеграла к вычислению работы переменной силы. Из школьного курса физики известно, что если материальная точка переместилась прямолинейно из точки Рассмотрим теперь применение определенного интеграла к вычислению работы переменной силы. Из школьного курса физики известно, что если материальная точка переместилась прямолинейно из точки  в точку в точку  на расстояние на расстояние  , а сила , а сила  , действующая на нее, направлена по прямой , действующая на нее, направлена по прямой  в сторону движения точки и имеет постоянную величину в сторону движения точки и имеет постоянную величину  , то работа этой силы на указанном участке движения , то работа этой силы на указанном участке движения  . Теперь допустим, что эта сила не постоянна по величине (направлена как и прежде), т.е. в разных точках траектории она имеет разные значения. Как вычислить работу такой переменной силы? Проведем через точки . Теперь допустим, что эта сила не постоянна по величине (направлена как и прежде), т.е. в разных точках траектории она имеет разные значения. Как вычислить работу такой переменной силы? Проведем через точки  и и  числовую ось числовую ось  , пусть эти точки соответствуют числам , пусть эти точки соответствуют числам  и и  на этой оси (см. рисунок). В каждой точке траектории от на этой оси (см. рисунок). В каждой точке траектории от  к к  на точку действует сила переменной величины на точку действует сила переменной величины 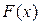 , зависящей от положения точки, т.е. от координаты , зависящей от положения точки, т.е. от координаты  этой точки. Тогда работа этой силы на указанном пути от этой точки. Тогда работа этой силы на указанном пути от  к к  вычисляется с помощью интеграла: вычисляется с помощью интеграла:
(3)  . .
Пример 4. В точке О начало координат числовой оси х закреплен положительный заряд величиной  . Свободный положительный заряд величины . Свободный положительный заряд величины  под действием кулоновской силы отталкивания от закрепленного заряда переместился вдоль оси х от точки с координатой под действием кулоновской силы отталкивания от закрепленного заряда переместился вдоль оси х от точки с координатой  ( ( ) в точку с координатой ) в точку с координатой  (см. рисунок). Найти работу силы Кулона на этом перемещении. (см. рисунок). Найти работу силы Кулона на этом перемещении.
 Решение. По закону Кулона сила, действующая на подвижный заряд Решение. По закону Кулона сила, действующая на подвижный заряд  со стороны неподвижного заряда со стороны неподвижного заряда  вычисляется по формуле вычисляется по формуле  , где , где  − расстояние между зарядами величины − расстояние между зарядами величины  и и  , ,  , а , а  Ф/м − так называемая электрическая постоянная. Поскольку текущая координата Ф/м − так называемая электрическая постоянная. Поскольку текущая координата  подвижного заряда подвижного заряда  и определяет расстояние между зарядами, то переменная сила Кулона, действующая на заряд и определяет расстояние между зарядами, то переменная сила Кулона, действующая на заряд  , будет иметь вид , будет иметь вид  . Поэтому по формуле (3) работа этой силы равна: . Поэтому по формуле (3) работа этой силы равна:
  . .
Итак, искомая работа 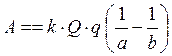 . .
Несобственные интегралы
При изучении определенного интеграла мы рассматривали только непрерывные на отрезке [ a,b ] функции, причем отрезок [ a,b ] был конечной длины (т.е. a≠−∞, b≠+∞). Непрерывные функции мы рассматривали по той причине, что, как писалось выше, для таких функций (хотя и не только для таких, но для таких − точно) существуют первообразные, а потому и неопределенный и определенный интеграл. Попробуем отойти от этих ограничений для подынтегральной функции в определенном интеграле.
Пусть подынтегральная функция имеет на отрезке [ a,b ] конечное число точек разрыва 1 рода (скачки). На рисунке в качестве примера изображен график функции  , имеющей одну точку разрыва 1 рода , имеющей одну точку разрыва 1 рода  . Для определения понятия определенного интеграла от такой функции по отрезку . Для определения понятия определенного интеграла от такой функции по отрезку  используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке  ) функции ) функции  по отрезку по отрезку  следующим образом: следующим образом:
(1)  . .
На каждом из отрезков  и и  подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции. подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции.
Пример 1. Вычислить  от функции от функции  , заданной двумя формулами (на разных участках изменения аргумента , заданной двумя формулами (на разных участках изменения аргумента  ): ):  . .
 Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций  и и  над соответствующими интервалами оси над соответствующими интервалами оси  . На интервале интегрирования . На интервале интегрирования  имеется одна точка разрыва 1 рода имеется одна точка разрыва 1 рода 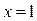 . Поэтому по определению (1): . Поэтому по определению (1):
 = { на каждом из интервалов интегрирования = { на каждом из интервалов интегрирования  и и  имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } = имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } =   Таким образом, Таким образом, 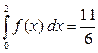 . .
Если же подынтегральная функция имеет на отрезке [ a,b ] точки разрыва 2-го рода (бесконечные скачки), то в обычном смысле определенный интеграл по этому отрезку уже не существует. Однако для некоторых из них все же можно ввести разумное понятие определенного интеграла, который будет называться несобственным интегралом 2 рода.
Если же подынтегральная функция непрерывна, но неограничен сам отрезок интегрирования (т.е.. a=−∞ и/или b=+∞), то интеграл в обычном смысле тоже не определен. Но опять же можно ввести для некоторых функций разумное понятие определенного интеграла и по бесконечному промежутку, который будет называться несобственным интегралом 1 рода. Остановимся на этом интеграле подробнее. Пусть функция  непрерывна на бесконечном интервале [ a,+∞). Можно ли разумно ввести понятие определенного интеграла по этому интервалу непрерывна на бесконечном интервале [ a,+∞). Можно ли разумно ввести понятие определенного интеграла по этому интервалу  ? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда ? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда  да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как  ). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел ). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел  . Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла . Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла  . Перейдем к точным определениям. . Перейдем к точным определениям.
Выражение вида  называется несобственным интегралом (1-го рода). Если существует конечный предел называется несобственным интегралом (1-го рода). Если существует конечный предел  , то несобственный интеграл , то несобственный интеграл  называется сходящимся, а число S называется его значением. Таким образом, можно по определению записать называется сходящимся, а число S называется его значением. Таким образом, можно по определению записать
(2)  = =  . .
Если же такой предел в правой части (2) не существует (или он равен бесконечности), то несобственный интеграл  называется расходящимся и ему не приписывается никакое числовое значение. называется расходящимся и ему не приписывается никакое числовое значение.
Таким образом, для вычисления несобственного интеграла (1-го рода)  используется следующая схема: используется следующая схема:
1) верхний предел +∞ заменить буквой b и вычислить получившийся интеграл (в ответ, конечно, будет входить буква b);
2) в ответе перейти к пределу при b→+∞.
Если предел существует, то интеграл сходится, а его значение равно значению получившегося предела. Если предел не существует, то интеграл расходится.
Пример 2. Выяснить, при каких значениях параметра  несобственный интеграл несобственный интеграл  сходится, а при каких расходится. сходится, а при каких расходится.
Решение. По изложенной выше схеме вычисляем  для произвольного значения положительного параметра для произвольного значения положительного параметра  , а затем в полученном выражении переходим к пределу при b→+∞. Поскольку неопределенный интеграл от функции , а затем в полученном выражении переходим к пределу при b→+∞. Поскольку неопределенный интеграл от функции  имеет разный вид для имеет разный вид для  и и  , то придется рассмотреть отдельно два этих случая. , то придется рассмотреть отдельно два этих случая.
1) Пусть  . Тогда . Тогда  . Поскольку . Поскольку  , то, по введенному выше определению, , то, по введенному выше определению,  при при  расходится. расходится.
2) Пусть  . Тогда . Тогда 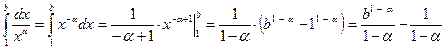 . Теперь надо в этом выражении перейти к пределу при b→+∞: . Теперь надо в этом выражении перейти к пределу при b→+∞:    {поскольку от {поскольку от  зависит только числитель в первом пределе}= зависит только числитель в первом пределе}= 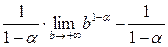 . Поэтому при . Поэтому при  : :
(3)   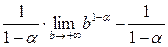 . .
Для вычисления  в (3) придется опять различать 2 случая: в (3) придется опять различать 2 случая:  и и  . .
а) Пусть  . Тогда . Тогда   . Поскольку . Поскольку  , то , то  , поэтому , поэтому  , а потому , а потому  . Поэтому при . Поэтому при  предел в (3) существует: предел в (3) существует:    . Следовательно, при . Следовательно, при  интеграл интеграл  сходится, причем его значение сходится, причем его значение  . .
б) Пусть  . Тогда в (3) . Тогда в (3)  , поскольку показатель степени , поскольку показатель степени  . Поэтому при . Поэтому при  предел в (3) равен бесконечности: предел в (3) равен бесконечности:   . Следовательно, при . Следовательно, при  интеграл интеграл  расходится. расходится.
Таким образом,  расходится при расходится при  , а при , а при  он сходится: он сходится:  . .
Точно так же с аналогичными определениями сходимости-расходимости вводится несобственный интеграл (1 рода), у которого верхний предел конечен, а нижний предел равен −∞:
(4)  = =  . .
Определим теперь несобственный интеграл от непрерывной функции по всей числовой прямой (−∞,+∞). Поскольку вводимые несобственные интегралы должны по свойствам походить на обычные, то желательно, чтобы выполнялось свойство:  , которое можно взять в качестве определения несобственного интеграла , которое можно взять в качестве определения несобственного интеграла  . Если сходятся оба несобственных интеграла . Если сходятся оба несобственных интеграла  и и  , то несобственный интеграл , то несобственный интеграл  называется сходящимся, а его значение принимается равным сумме интегралов: называется сходящимся, а его значение принимается равным сумме интегралов:
(5)  . .
Если же хотя бы один из интегралов  или или  расходится, то интеграл расходится, то интеграл  называется расходящимся. называется расходящимся.
Пример 3. Сходится ли интеграл  ? ?
Решение. По определению (4) нужно выяснить, существует ли конечный предел  . Вычислим интеграл под знаком предела, учитывая, что . Вычислим интеграл под знаком предела, учитывая, что  : :    . Тогда . Тогда  . Поэтому . Поэтому  расходится. расходится.
Пример 4. Вычислить  . .
Решение. По формуле (4):
    ={ с учетом, что ={ с учетом, что  } }  . Таким образом, интеграл сходится и . Таким образом, интеграл сходится и  . .
Пример 5. Вычислить  . .
Решение. По формуле (5):
(6)  , ,
причем, если хотя бы один из несобственных интегралов в правой части расходится, то и сам интеграл  считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов: считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов:  . Вычисляем интеграл под знаком предела: . Вычисляем интеграл под знаком предела:  ={ на интервале интегрирования ={ на интервале интегрирования  переменная интегрирования переменная интегрирования  , а потому , а потому  можно заменить на можно заменить на  }= }=  {используем формулу {используем формулу  при при  и и  } }  . Поэтому . Поэтому   (использовали, что (использовали, что  , так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6): , так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6):  . Имеем: . Имеем:  ={ на интервале интегрирования ={ на интервале интегрирования  переменная интегрирования переменная интегрирования  , а потому , а потому  можно заменить на можно заменить на  }= }=    . Поэтому . Поэтому   . Таким образом, исходный интеграл сходится, а согласно (6): . Таким образом, исходный интеграл сходится, а согласно (6):  . .
|



 на отрезке [ a,b ], лежащий над осью
на отрезке [ a,b ], лежащий над осью  . Рассмотрим снова криволинейную трапецию, основанием которой является
. Рассмотрим снова криволинейную трапецию, основанием которой является  отрезок [ a,b ], боковыми сторонами являются отрезки вертикальных прямых, проходящих через точки (числа) a и b на оси
отрезок [ a,b ], боковыми сторонами являются отрезки вертикальных прямых, проходящих через точки (числа) a и b на оси  , но сейчас нас площадь не интересует. Если эту криволинейную трапецию вращать вокруг оси
, но сейчас нас площадь не интересует. Если эту криволинейную трапецию вращать вокруг оси  .
. для объема прямого кругового конуса высоты
для объема прямого кругового конуса высоты  и радиуса основания
и радиуса основания  .
. Решение. Для того, чтобы воспользоваться формулой (1), представим упомянутый конус высоты
Решение. Для того, чтобы воспользоваться формулой (1), представим упомянутый конус высоты  , изображенного на рисунке. В этом треугольнике длина катета
, изображенного на рисунке. В этом треугольнике длина катета  равна высоте конуса
равна высоте конуса  на оси
на оси  и
и  . Осталось понять, какое выражение подставлять в (1) вместо
. Осталось понять, какое выражение подставлять в (1) вместо  . В формуле (1)
. В формуле (1)  . Как известно, все наклонные прямые имеют уравнение вида
. Как известно, все наклонные прямые имеют уравнение вида  . Найдем числа
. Найдем числа  и
и  для прямой
для прямой 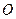 , то
, то  , а потому уравнение прямой
, а потому уравнение прямой  . Число
. Число  наклона прямой к оси
наклона прямой к оси  . Итак, уравнение прямой
. Итак, уравнение прямой  , а потому в нашем примере в качестве
, а потому в нашем примере в качестве  . Таким образом, искомый объем конуса выражается определенным интегралом
. Таким образом, искомый объем конуса выражается определенным интегралом  . Вычислим его, учитывая что высота
. Вычислим его, учитывая что высота 
 Пример 2. Найти объем тела, образованного вращением вокруг оси х фигуры, ограниченной графиками функций
Пример 2. Найти объем тела, образованного вращением вокруг оси х фигуры, ограниченной графиками функций  и
и  (см. рисунок).
(см. рисунок). , где
, где  и
и  есть объемы описанных выше тел вращения. Второе тело вращения (полученное вращением прямоугольного треугольника) есть, очевидно, прямой круговой конус с высотой
есть объемы описанных выше тел вращения. Второе тело вращения (полученное вращением прямоугольного треугольника) есть, очевидно, прямой круговой конус с высотой  и радиусом основания
и радиусом основания  (см. рисунок). Поэтому его объем
(см. рисунок). Поэтому его объем  . Объем
. Объем  . Таким образом, искомый объем
. Таким образом, искомый объем  кубических единиц.
кубических единиц. Рассмотрим применение определенного интеграла к вычислению длины дуги кривой. Пусть дуга
Рассмотрим применение определенного интеграла к вычислению длины дуги кривой. Пусть дуга  некоторой кривой является частью графика непрерывной функции
некоторой кривой является частью графика непрерывной функции  при изменении
при изменении 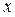 на отрезке
на отрезке  (см. рисунок). Числа
(см. рисунок). Числа  и
и  являются абсциссами (т.е. х -координатами) начальной
являются абсциссами (т.е. х -координатами) начальной  и конечной
и конечной  точки дуги
точки дуги  . В этом случае длина
. В этом случае длина  дуги
дуги  .
. (так называемая полукубическая парабола), если
(так называемая полукубическая парабола), если  .
. ,
,  ,
, 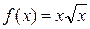 . Для удобства преобразуем выражение для функции:
. Для удобства преобразуем выражение для функции:  . Тогда
. Тогда  . По формуле (2) длина кривой
. По формуле (2) длина кривой 
 {вносим
{вносим  под знак дифференциала, добавляя перед интегралом поправочный множитель
под знак дифференциала, добавляя перед интегралом поправочный множитель 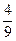 }
} 
 . Итак,
. Итак,  .
. Рассмотрим теперь применение определенного интеграла к вычислению работы переменной силы. Из школьного курса физики известно, что если материальная точка переместилась прямолинейно из точки
Рассмотрим теперь применение определенного интеграла к вычислению работы переменной силы. Из школьного курса физики известно, что если материальная точка переместилась прямолинейно из точки  , а сила
, а сила  , действующая на нее, направлена по прямой
, действующая на нее, направлена по прямой  в сторону движения точки и имеет постоянную величину
в сторону движения точки и имеет постоянную величину  , то работа этой силы на указанном участке движения
, то работа этой силы на указанном участке движения  . Теперь допустим, что эта сила не постоянна по величине (направлена как и прежде), т.е. в разных точках траектории она имеет разные значения. Как вычислить работу такой переменной силы? Проведем через точки
. Теперь допустим, что эта сила не постоянна по величине (направлена как и прежде), т.е. в разных точках траектории она имеет разные значения. Как вычислить работу такой переменной силы? Проведем через точки  , пусть эти точки соответствуют числам
, пусть эти точки соответствуют числам  и
и 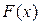 , зависящей от положения точки, т.е. от координаты
, зависящей от положения точки, т.е. от координаты  этой точки. Тогда работа этой силы на указанном пути от
этой точки. Тогда работа этой силы на указанном пути от  .
. . Свободный положительный заряд величины
. Свободный положительный заряд величины  под действием кулоновской силы отталкивания от закрепленного заряда переместился вдоль оси х от точки с координатой
под действием кулоновской силы отталкивания от закрепленного заряда переместился вдоль оси х от точки с координатой  (
( ) в точку с координатой
) в точку с координатой  (см. рисунок). Найти работу силы Кулона на этом перемещении.
(см. рисунок). Найти работу силы Кулона на этом перемещении. Решение. По закону Кулона сила, действующая на подвижный заряд
Решение. По закону Кулона сила, действующая на подвижный заряд  со стороны неподвижного заряда
со стороны неподвижного заряда  вычисляется по формуле
вычисляется по формуле  , где
, где  − расстояние между зарядами величины
− расстояние между зарядами величины  , а
, а  Ф/м − так называемая электрическая постоянная. Поскольку текущая координата
Ф/м − так называемая электрическая постоянная. Поскольку текущая координата  подвижного заряда
подвижного заряда  . Поэтому по формуле (3) работа этой силы равна:
. Поэтому по формуле (3) работа этой силы равна:
 .
.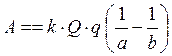 .
. , имеющей одну точку разрыва 1 рода
, имеющей одну точку разрыва 1 рода  . Для определения понятия определенного интеграла от такой функции по отрезку
. Для определения понятия определенного интеграла от такой функции по отрезку  используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке
используем последнее свойство определенных интегралов от непрерывных функций: если отрезок интегрирования разбит на 2 части, то интеграл по всему отрезку равен сумме интегралов по составляющим этот отрезок частям. Определим теперь интеграл от разрывной (в точке  по отрезку
по отрезку  .
. и
и  подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции.
подынтегральная функция непрерывна (если доопределить ее на концах отрезка соответствующими предельными значениями), а потому определенные интегралы в правой части формулы (1) по этим отрезкам существуют. В формуле (1) правая часть служит определением левой части. В случае нескольких точек разрыва 1 рода интеграл определяется аналогично как сумма интегралов по отрезкам непрерывности функции. от функции
от функции  ):
):  .
. Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций
Решение. График этой функции (на рисунке) «склеен» из кусков графиков функций  и
и  над соответствующими интервалами оси
над соответствующими интервалами оси  имеется одна точка разрыва 1 рода
имеется одна точка разрыва 1 рода 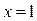 . Поэтому по определению (1):
. Поэтому по определению (1): = { на каждом из интервалов интегрирования
= { на каждом из интервалов интегрирования  и
и  имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } =
имеется свое выражение для функции, которое и подставляем в соответствующий интеграл } = 
 Таким образом,
Таким образом, 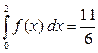 .
. ? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда
? По геометрическому смыслу определенного интеграла (площадь соответствующей криволинейной трапеции) интеграл такого типа должен иметь смысл площади неограниченной криволинейной трапеции, изображенной на рисунке. Но может ли площадь неограниченной фигуры быть конечным числом, а не бесконечностью? Иногда  да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как
да, а иногда нет. Как же можно определить площадь неограниченной фигуры, изображенной на рисунке? Можно поступить, например, так. Возьмем некоторое число b > a и обрежем эту фигуру вертикальной прямой, проходящей через число b на оси х. Площадь оставшейся слева фигуры (уже ограниченной) есть какое-то конечное число (которое, по геометрическому смыслу интеграла, можно вычислить как  ). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел
). Будем теперь безгранично отодвигать вправо построенную правую вертикальную границу фигуры (что соответствует предельному переходу b→+∞). Может при этом возникнуть две ситуации. Либо площади фигур при таком процессе не приближаются ни к какому числу (или неограниченно растут до бесконечности). Либо эти площади неограниченно приближаются к некоторому числу (обозначим его S), т.е. существует конечный предел  . Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла
. Тогда естественно это число S считать площадью исходной неограниченной криволинейной трапеции и значением интеграла  . Перейдем к точным определениям.
. Перейдем к точным определениям. , то несобственный интеграл
, то несобственный интеграл  =
=  .
. несобственный интеграл
несобственный интеграл  сходится, а при каких расходится.
сходится, а при каких расходится. для произвольного значения положительного параметра
для произвольного значения положительного параметра  имеет разный вид для
имеет разный вид для  и
и  , то придется рассмотреть отдельно два этих случая.
, то придется рассмотреть отдельно два этих случая. . Поскольку
. Поскольку  , то, по введенному выше определению,
, то, по введенному выше определению, 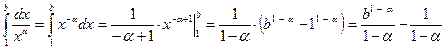 . Теперь надо в этом выражении перейти к пределу при b→+∞:
. Теперь надо в этом выражении перейти к пределу при b→+∞: 

 {поскольку от
{поскольку от 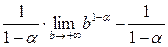 . Поэтому при
. Поэтому при 

 в (3) придется опять различать 2 случая:
в (3) придется опять различать 2 случая:  и
и  .
.
 . Поскольку
. Поскольку  , поэтому
, поэтому  , а потому
, а потому  . Поэтому при
. Поэтому при  . Следовательно, при
. Следовательно, при  сходится, причем его значение
сходится, причем его значение  .
. , поскольку показатель степени
, поскольку показатель степени  . Поэтому при
. Поэтому при  . Следовательно, при
. Следовательно, при  расходится.
расходится. , а при
, а при  =
=  .
. , которое можно взять в качестве определения несобственного интеграла
, которое можно взять в качестве определения несобственного интеграла  . Если сходятся оба несобственных интеграла
. Если сходятся оба несобственных интеграла  и
и  , то несобственный интеграл
, то несобственный интеграл  ?
? . Вычислим интеграл под знаком предела, учитывая, что
. Вычислим интеграл под знаком предела, учитывая, что  :
: 

 . Тогда
. Тогда  . Поэтому
. Поэтому  .
.


 ={ с учетом, что
={ с учетом, что  }
}  . Таким образом, интеграл сходится и
. Таким образом, интеграл сходится и  .
. .
. ,
, считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов:
считается расходящимся. Вычислим отдельно каждый из упомянутых интегралов:  . Вычисляем интеграл под знаком предела:
. Вычисляем интеграл под знаком предела:  ={ на интервале интегрирования
={ на интервале интегрирования  переменная интегрирования
переменная интегрирования  , а потому
, а потому  можно заменить на
можно заменить на  {используем формулу
{используем формулу  при
при  и
и  . Поэтому
. Поэтому 
 (использовали, что
(использовали, что  , так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6):
, так как при стремлении показателя степени к минус бесконечности экспонента стремится к нулю). Вычисляем первый интеграл в правой части (6):  . Имеем:
. Имеем:  ={ на интервале интегрирования
={ на интервале интегрирования  переменная интегрирования
переменная интегрирования  , а потому
, а потому  }=
}= 

 . Поэтому
. Поэтому 
 . Таким образом, исходный интеграл сходится, а согласно (6):
. Таким образом, исходный интеграл сходится, а согласно (6):  .
.


