
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена переменной и интегрирование по частям в определенном интегралеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Самым простым методом вычисления неопределенных интегралов был так называемый метод непосредственного интегрирования, сводящийся к преобразованию подынтегрального выражения к сумме-разности элементарных функций из таблицы интегралов с некоторыми числовыми коэффициентами. Если же это не удавалось, то предлагались два специальных приема – замена переменной и интегрирование по частям. Ситуация с вычислением определенных интегралов в точности та же самая. Имеется практически точно такой же метод непосредственного интегрирования определенных интегралов, который от того же метода для неопределенных интегралов отличается лишь на последнем этапе − тем, что после сведения задачи к интегрированию «табличных» функций при их последующем интегрировании мы после выписывания соответствующей первообразной Теорема. Пусть
Доказательство теоремы несложно, проводится с помощью формулы Правила для пересчетов пределов интегрирования следующие. 1. Если при замене переменной старая переменная выражена через новую в форме 2. Если при замене переменной новая переменная выражена через старую в форме Советы о том, какая замена целесообразна для вычисления того или иного интеграла, − те же самые, что и при вычислении неопределённых интегралов, так что тут ничего нового изучать не придётся. Итак, два основных отличия от замены переменных в неопределенном интеграле состоят в том, что в ответе теперь не нужен возврат к старой переменной, зато добавляется работа по пересчету пределов интегрирования α и β для новой переменной. Пример 1. Вычислить Решение. В предыдущей главе (посвященной неопределенным интегралам) в конце параграфа «Интегрирование некоторых иррациональных выражений» при интегрировании выражений, содержащих
= {применим формулу понижения степени Итак, Пример 2. Вычислить Решение. Для неопределенных интегралов, содержащих переменную интегрирования только под знаком экспоненты
Рассмотрим теперь метод интегрирования по частям в определенном интеграле. По форме он почти не отличается от аналогичного метода для неопределенных интегралов. Теорема. Пусть функции u(x) и v(x) имеют непрерывные производные на отрезке [ a,b ]. Тогда справедлива следующая формула интегрирования по частям: (1) Напомним формулу интегрирования по частям для неопределенного интеграла, приведенную в параграфе «Интегрирование по частям» предыдущей главы: (2) Видно, что отличия в формуле (1) от формулы (2) лишь в том, что интегралы справа и слева становятся определенными, а выражение 1. Пример 3. Вычислить Решение. Это второй из перечисленных выше типов интеграла, поэтому применяем формулу интегрирования по частям (1), беря в соответствии с рекомендацией
Пример 4. Вычислить Решение. Это интеграл первого из перечисленных выше типов при
Таким образом, Пример 5. Вычислить Решение. Представим интеграл в виде:
Итак,
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.151.211 (0.007 с.) |

 не приписываем дальше «+ С» (как при вычислении неопределенного интеграла), а, в соответствии с формулой Ньютона-Лейбница, вместо этого ставим вертикальную черту с пределами интегрирования
не приписываем дальше «+ С» (как при вычислении неопределенного интеграла), а, в соответствии с формулой Ньютона-Лейбница, вместо этого ставим вертикальную черту с пределами интегрирования  и считаем соответствующую разность значений первообразной. Примеры вычисления определенных интегралов методом непосредственного интегрирования приведены в предыдущих параграфах. Если же этот метод неприменим, снова используются методы замены переменной и интегрирования по частям, которые тоже очень похожи на эти же методы для неопределенного интеграла с небольшими изменениями. Такими же остаются и рекомендации по конкретным типам замены в зависимости от вида подынтегральной функции, а также по классам функций, при интегрировании которых применяется интегрирование по частям. Формулы, описывающие эти методы для случаев неопределенного и определенного интегралов, также очень похожи. Однако имеется некоторая их специфика для определенного интеграла, которая будет отмечена ниже. Начнем с формулы замены переменной, формальное изложение которой выглядит достаточно громоздко.
и считаем соответствующую разность значений первообразной. Примеры вычисления определенных интегралов методом непосредственного интегрирования приведены в предыдущих параграфах. Если же этот метод неприменим, снова используются методы замены переменной и интегрирования по частям, которые тоже очень похожи на эти же методы для неопределенного интеграла с небольшими изменениями. Такими же остаются и рекомендации по конкретным типам замены в зависимости от вида подынтегральной функции, а также по классам функций, при интегрировании которых применяется интегрирование по частям. Формулы, описывающие эти методы для случаев неопределенного и определенного интегралов, также очень похожи. Однако имеется некоторая их специфика для определенного интеграла, которая будет отмечена ниже. Начнем с формулы замены переменной, формальное изложение которой выглядит достаточно громоздко. непрерывна на отрезке [ a, b ].
непрерывна на отрезке [ a, b ]. имеет непрерывную производную на отрезке [ α, β ].
имеет непрерывную производную на отрезке [ α, β ]. ,
,  .
. .
. находится из условия
находится из условия  , то
, то  , а
, а  .
. .
. , предлагалась замена переменной вида
, предлагалась замена переменной вида 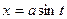 . Такого же вида замену сделаем и сейчас, не забывая пересчитать пределы интегрирования α и β для новой переменной по приведенному выше правилу 1.
. Такого же вида замену сделаем и сейчас, не забывая пересчитать пределы интегрирования α и β для новой переменной по приведенному выше правилу 1.
 } =
} = 

 .
. .
. .
. , рекомендовалась замена переменной по формуле
, рекомендовалась замена переменной по формуле 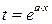 . Поэтому в данном примере надо бы сдеать замену переменной по формуле
. Поэтому в данном примере надо бы сдеать замену переменной по формуле  . Однако в данном случае решение будет короче, если сделать замену
. Однако в данном случае решение будет короче, если сделать замену  (так как именно такое выражение стоит под знаком корня в интеграле). Пересчет пределов интегрирования α и β для новой переменной выполняем по правилу 2.
(так как именно такое выражение стоит под знаком корня в интеграле). Пересчет пределов интегрирования α и β для новой переменной выполняем по правилу 2.
 . Итак,
. Итак,  .
.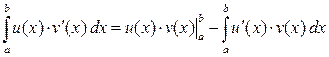 .
. .
. заменяется на
заменяется на  , что, как обычно, означает разность значений при
, что, как обычно, означает разность значений при  и
и  выражения слева от вертикальной черты. В том же параграфе предыдущей главы были приведены типы интегралов, для вычисления которых следует применять метод интегрирования по частям, а так же рекомендации, что при этом брать за
выражения слева от вертикальной черты. В том же параграфе предыдущей главы были приведены типы интегралов, для вычисления которых следует применять метод интегрирования по частям, а так же рекомендации, что при этом брать за  , а что за
, а что за  . Все эти рекомендации справедливы и при вычислении определенных интегралов:
. Все эти рекомендации справедливы и при вычислении определенных интегралов: 2.
2.  3.
3.  4.
4. 
 .
. за
за  , а
, а  за
за 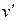 :
:
 . Итак,
. Итак,  .
. .
.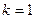 и
и  , поэтому при применении формулы (1) делаем рекомендуемый выбор функций
, поэтому при применении формулы (1) делаем рекомендуемый выбор функций 

 { учтем, что
{ учтем, что  }
}  .
. .
. .
. . Теперь видно, что это интеграл третьего типа при
. Теперь видно, что это интеграл третьего типа при 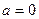 (так как
(так как  ),
),  и
и 

 {учтем, что
{учтем, что  , а
, а  }
}  .
. .
.


