
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение с разделенными переменнымиСодержание книги
Поиск на нашем сайте
Далеко не для всякого дифференциального уравнения первого порядка разработан алгоритм получения его общего решения. Однако для многих типов уравнений такие алгоритмы есть, и мы на некоторых из них в этом пособии остановимся. Прежде всего, это так называемые уравнения с разделенными переменными. Это такое уравнение в дифференциалах (1) Иногда удобнее такое уравнение с разделенными переменными записывать в форме (2) Очевидно, что уравнение вида (1) легко приводится к уравнению вида (2) Если формально «навесить» значки неопределенного интеграла перед правой и левой частью уравнения (2), то получим (3) Допустим, нам удалось вычислить эти интегралы: (4) Можно доказать, что описанные формальные действия с уравнением (2) действительно приводят к получению его общего интеграла, которым и является выражение (4). Обосновывает это следующая Теорема. Функциональные уравнения (2) и (4) эквивалентны. Утверждение теоремы следует понимать в том смысле, что любое решение дифференциального уравнения (2) (как вида Доказательство этой теоремы несложное. Докажем, например, что если функция (*) Поскольку Таким образом, для получения общего интеграла уравнения с разделенными переменными вида (2) можно использовать следующую схему. 1. Формально «навесить» значок неопределенного интеграла на левую и правую часть уравнения (2). 2. Вычислить и приравнять полученные интегралы, но при этом «+С» оставить только при вычислении интеграла по переменной 3. Если в полученном выражении удастся переменную Пример. Найти общее решение уравнения Решение. Это уравнение с разделенными переменными вида (1), но оно легко сводится к уравнению вида (2):
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

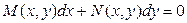 , у которого функция
, у которого функция 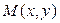 при
при 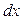 на самом деле зависит только от
на самом деле зависит только от  , функция
, функция 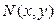 при
при 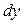 зависит только от
зависит только от  . Таким образом, уравнением с разделенными переменными называется уравнение в дифференциальной форме вида
. Таким образом, уравнением с разделенными переменными называется уравнение в дифференциальной форме вида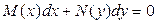 .
.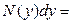
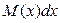 .
.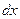 в правую часть) и наоборот. Поэтому уравнение вида (2) тоже будем называть уравнением с разделенными переменными.
в правую часть) и наоборот. Поэтому уравнение вида (2) тоже будем называть уравнением с разделенными переменными.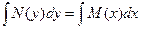 .
. ,
,  . Если теперь формально подставить в (3) вместо интегралов полученные выражения для них, но в интеграле слева «+ С» не писать, то получим
. Если теперь формально подставить в (3) вместо интегралов полученные выражения для них, но в интеграле слева «+ С» не писать, то получим .
. , так и
, так и  ) является также решением функционального уравнения (4). И наоборот.
) является также решением функционального уравнения (4). И наоборот. . Вычислим производные от правой и левой части этого тождества (вспоминая формулу производной от сложной функции при дифференцировании левой части):
. Вычислим производные от правой и левой части этого тождества (вспоминая формулу производной от сложной функции при дифференцировании левой части):  или (производная от хотя и произвольной, но все же постоянной равна 0)
или (производная от хотя и произвольной, но все же постоянной равна 0) .
. и
и  являются первообразными для
являются первообразными для  и
и  соответственно, т.е.
соответственно, т.е.  ,
, 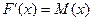 . Тогда из (*) получим тождество
. Тогда из (*) получим тождество  . Умножим обе части на произвольное число
. Умножим обе части на произвольное число  ):
):  . Учитывая, что по определению
. Учитывая, что по определению  , получаем, что для всех
, получаем, что для всех  , что означает, что функция
, что означает, что функция 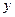 выразить через
выразить через 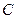 , то получим общее решение уравнения (2).
, то получим общее решение уравнения (2). .
. . Согласно изложенной выше схеме, «навешиваем» на обе части неопределенные интегралы и вычисляем их:
. Согласно изложенной выше схеме, «навешиваем» на обе части неопределенные интегралы и вычисляем их: ,
,  . Получили общий интеграл уравнения (т.е. выражение, связывающее
. Получили общий интеграл уравнения (т.е. выражение, связывающее  ,
, 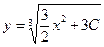 . В этом выражении
. В этом выражении  − произвольная постоянная, меняющаяся от
− произвольная постоянная, меняющаяся от 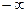 до
до  . При этом, очевидно,
. При этом, очевидно, 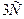 тоже будет меняться от
тоже будет меняться от  можно снова записать
можно снова записать 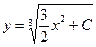 .
.


