Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о площади криволинейной трапецииСодержание книги
Поиск на нашем сайте
Рассмотрим на координатной плоскости хОу следующий четырехугольник с одной криволинейной границей. Основанием четырехугольника является некоторый отрезок [ a,b ] на числовой оси х. Боковыми сторонами являются отрезки вертикальных прямых, проходящих через точки (числа) a и b на оси х. А вот верхнее основание сделаем криволинейным. Но надо эту кривую границу как-то определить. Мы помним, что разнообразные кривые нам давали графики различных функций. Поэтому будем считать, что верхнее основание есть кусок графика некоторой функции
в правой части этого приближенного равенства называется интегральной суммой для функции Посмотрим, как поведет себя величина этой погрешности, если, скажем, увеличить число разбиений исходного отрезка вдвое (вместо n взять 2n). Тогда в середину каждого старого отрезка попадет еще один узел. Легко убедиться, что в этом случае часть неучтенных площадей старых «криволинейных» треугольников учтется, а новая приближенная формула (1) Хотя мы и получили точную формулу для площади криволинейной трапеции, она мало пригодна для практического применения по следующим причинам. Во-первых, мы никогда не сможем взять n = ∞, мы можем взять n только конечным (хотя и большим), а потому нам опять останется возможность пользоваться только приближенной формулой Пусть функция (2) Числа Замечание. В большинстве учебников дается более общее и более сложное определение определенного интеграла. Однако для непрерывных функций эти определения эквивалентны, а именно такие функции мы пока и рассматриваем. Сравнивая точную формулу (1) для площади S криволинейной трапеции и формулу (2), определяющую интеграл, можно записать: (3) Формула Ньютона-Лейбница О каком же простом способе вычисления определенного интеграла шла речь выше? Ответ на этот вопрос дает знаменитая формула Ньютона-Лейбница, которая указывает на тесную связь неопределенного и определенного интегралов. Имеет место следующая Теорема (формула Ньютона-Лейбница). Пусть функция (1) Для того чтобы сделать эту формулу еще более компактной, ввели следующее обозначение для разности (2) Таким образом, формула Ньютона-Лейбница (1) принимает с учетом обозначения (2) следующий окончательный вид: (3) Формула Ньютона-Лейбница утверждает, что для вычисления определенного интеграла от некоторой функции достаточно найти ее первообразную (т.е. фактически найти неопределенный интеграл) и взять разность ее значений на концах интервала. Однако, как мы увидим дальше, этот путь предварительного вычисления неопределенного интеграла нецелесообразен и приводит во многих случаях к лишней работе. Поэтому при вычислении определенного интеграла пользуются теми же приемами, что и при вычислении неопределенного интеграла, учитывая их специфику для определенного интеграла, о которой будет сказано позже. Итак, площадь криволинейной трапеции выражается через определенный интеграл Пример. Найти площадь под одним витком синусоиды. Решение.
Таким образом, площадь под одним витком синусоиды равна 2 квадратным единицам. Далее будет приведена формула, которая позволяет с помощью определенного интеграла вычислять площади фигур со многими криволинейными границами.
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |


 ,непрерывной на отрезке [ a,b ]. Такой «четырехугольник» называется криволинейной трапецией (см. рисунок). Поставим себе задачу найти формулу для вычисления его площади, которую обозначим буквой S. Поскольку точной формулы для вычисления площади такой фигуры у нас нет, то на первом этапе поставим целью найти хотя бы приближенную формулу для S. Идея такая. Попробуем достаточно плотно заполнить криволинейную трапецию, например, прямоугольниками (так как формула для вычисления их площадей известна) и посчитаем сумму их площадей. Получим приближенное (так как эти прямоугольники не смогут заполнить всю криволинейную трапецию) значение для S. Прямоугольники построим следующим образом. Разделим отрезок [ a,b ] на n равных частей точками a = x0 < x1 < x2 < … < xn = b (см. рисунок, соответствующий n= 5). Число разбиений n потом будет меняться. Проведем через каждую точку деления (узел) вертикальный отрезок до пересечения с графиком функции
,непрерывной на отрезке [ a,b ]. Такой «четырехугольник» называется криволинейной трапецией (см. рисунок). Поставим себе задачу найти формулу для вычисления его площади, которую обозначим буквой S. Поскольку точной формулы для вычисления площади такой фигуры у нас нет, то на первом этапе поставим целью найти хотя бы приближенную формулу для S. Идея такая. Попробуем достаточно плотно заполнить криволинейную трапецию, например, прямоугольниками (так как формула для вычисления их площадей известна) и посчитаем сумму их площадей. Получим приближенное (так как эти прямоугольники не смогут заполнить всю криволинейную трапецию) значение для S. Прямоугольники построим следующим образом. Разделим отрезок [ a,b ] на n равных частей точками a = x0 < x1 < x2 < … < xn = b (см. рисунок, соответствующий n= 5). Число разбиений n потом будет меняться. Проведем через каждую точку деления (узел) вертикальный отрезок до пересечения с графиком функции  преимущество каждой из них в том, что криволинейные границы у них значительно меньше, чем у исходной криволинейной трапеции. Сейчас мы их вообще уберем, заменив маленькие криволинейные трапеции прямоугольниками (как на рисунке). Площадь прямоугольника равна произведению длин его сторон. Длина нижнего основания у всех прямоугольников одинакова и равна h = (b−a)/n (так как отрезок делился на n равных частей). Из рисунка видно, что длина второй стороны первого прямоугольника равна значению
преимущество каждой из них в том, что криволинейные границы у них значительно меньше, чем у исходной криволинейной трапеции. Сейчас мы их вообще уберем, заменив маленькие криволинейные трапеции прямоугольниками (как на рисунке). Площадь прямоугольника равна произведению длин его сторон. Длина нижнего основания у всех прямоугольников одинакова и равна h = (b−a)/n (так как отрезок делился на n равных частей). Из рисунка видно, что длина второй стороны первого прямоугольника равна значению 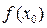 функции
функции  . Для второго прямоугольника длина этой стороны равна
. Для второго прямоугольника длина этой стороны равна 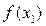 и т.д.. Площадь первой криволинейной трапеции приближенно равна площади первого прямоугольника:
и т.д.. Площадь первой криволинейной трапеции приближенно равна площади первого прямоугольника:  . Далее,
. Далее, 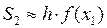 , …,
, …, 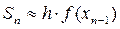 . Подставляя эти приближенные равенства в приведенную выше формулу
. Подставляя эти приближенные равенства в приведенную выше формулу  . Вынося h за скобку и подставляя его значение h = (b−a)/n, получаем
. Вынося h за скобку и подставляя его значение h = (b−a)/n, получаем  . Выражение
. Выражение
 окажется более точной. И чем больше берется число разбиений, тем точнее становится формула. Если перейти в этой формуле к пределу при n → ∞, то в пределе «криволинейные» треугольники исчезнут, а формула для площади окажется точной. Итак, площадь криволинейной трапеции есть предел интегральных сумм, когда число разбиений отрезка [ a,b ] стремится к бесконечности, и выражается точной формулой:
окажется более точной. И чем больше берется число разбиений, тем точнее становится формула. Если перейти в этой формуле к пределу при n → ∞, то в пределе «криволинейные» треугольники исчезнут, а формула для площади окажется точной. Итак, площадь криволинейной трапеции есть предел интегральных сумм, когда число разбиений отрезка [ a,b ] стремится к бесконечности, и выражается точной формулой: .
. большого числа слагаемых, каждое из которых есть значение функции в некоторой точке. Если эта функция вычисляется по громоздкой формуле, то нас ждет слишком утомительная вычислительная работа. Поэтому исторически возникала необходимость найти простой способ вычисления пределов вида
большого числа слагаемых, каждое из которых есть значение функции в некоторой точке. Если эта функция вычисляется по громоздкой формуле, то нас ждет слишком утомительная вычислительная работа. Поэтому исторически возникала необходимость найти простой способ вычисления пределов вида  в правой части (1). Такой способ был найден практически одновременно известными математиками Ньютоном и Лейбницем, а сами такие пределы получили название определенного интеграла. Перейдем к точным определениям.
в правой части (1). Такой способ был найден практически одновременно известными математиками Ньютоном и Лейбницем, а сами такие пределы получили название определенного интеграла. Перейдем к точным определениям.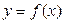 непрерывна на отрезке [ a,b ]. Определенным интегралом от функции
непрерывна на отрезке [ a,b ]. Определенным интегралом от функции  разбиений отрезка стремиться к бесконечности. Обозначение такого интеграла:
разбиений отрезка стремиться к бесконечности. Обозначение такого интеграла:  . Итак, по определению:
. Итак, по определению: .
. и
и  называются нижним и верхним пределами интегрирования.
называются нижним и верхним пределами интегрирования. .
.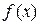 непрерывна на отрезке [ a,b ], функция
непрерывна на отрезке [ a,b ], функция  является ее первообразной (т.е.
является ее первообразной (т.е.  , а потому известен неопределенный интеграл:
, а потому известен неопределенный интеграл:  ). Тогда
). Тогда .
. в правой части формулы:
в правой части формулы: .
. .
. , а определенный интеграл вычисляется по формуле Ньютона-Лейбница (3). Попробуем теперь с помощью этих формул найти площадь фигуры, у которой ранее мы бы вычислить площадь не могли.
, а определенный интеграл вычисляется по формуле Ньютона-Лейбница (3). Попробуем теперь с помощью этих формул найти площадь фигуры, у которой ранее мы бы вычислить площадь не могли. Синусоида это график функции
Синусоида это график функции  . Имеется в виду площадь криволинейной трапеции между осью
. Имеется в виду площадь криволинейной трапеции между осью  и графиком
и графиком 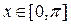 (см. рисунок). Используем формулу для площади
(см. рисунок). Используем формулу для площади  ,
,  ,
,  . Учтем, что
. Учтем, что 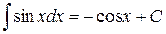 , а потому первообразная для
, а потому первообразная для  . Поэтому по формуле Ньютона-Лейбница (3) получаем:
. Поэтому по формуле Ньютона-Лейбница (3) получаем: .
.