
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения второго порядкаСодержание книги
Поиск на нашем сайте
(1) где Если правая часть уравнения (1) Рассмотрим сначала структуру общего решения однородного уравнения (2) Оказывается, чтобы найти все решения такого уравнения, достаточно найти только любые два его решения с тем единственным условием, чтобы эти решения были линейно независимы. Познакомимся с этим понятием. Назовем две функции (3) для всех Пример 1. Доказать, что функции Решение. Докажем методом «от противного». Предположим, что на некотором интервале функции Пример 2. Доказать, что функции Решение. Предположив, что на некотором интервале функции Пример 3. Доказать, что функции Решение. Предположив, что на некотором интервале эти функции линейно зависимы, получим из (3), что Назовем пару функций Теорема 1. Пусть (4) где Доказательство. Согласно определению общего решения уравнения 2-го порядка (см. параграф «Дифференциальные уравнения 2-го порядка» после формулы (3)), для доказательства того, что выражение (4) является таковым для уравнения (2), необходимо показать два факта: 1) Выражение (4) зависит от двух (это существенно! – см. замечание 2 ниже) произвольных постоянных 2) При любых числовых значениях Первый факт, очевидно, сразу следует из вида выражения (4). Перед доказательством второго факта отметим, что, поскольку (5) А теперь проверим второй упомянутый выше факт. Пусть Таким образом, справедливо следующее Правило 1. Для нахождения общего решения однородного уравнения (2) достаточно найти любые два его линейно независимых решения Замечание 1. Можно показать, что общее решение (4) уравнения (2) содержит все решения этого уравнения. Это означает, что любое решение уравнения (2) имеет вид (4) с некоторыми конкретными числовыми значениями произвольных постоянных Замечание 2. Отметим существенность линейной независимости решений Теперь перейдем к изучению структуры общего решения неоднородного уравнения (1): Теорема 2. Общее решение неоднородного уравнения (1) равно сумме общего решения соответствующего однородного уравнения (2) и какого-либо частного решения самого неоднородного уравнения (1). Учитывая, что общее решение однородного уравнения (2) имеет (как доказано в теореме 1) вид (4), можно утверждать, что общее решение неоднородного уравнения (1) имеет вид: (6) где Доказательство. Требуется доказать, что формула (6) дает общее решение уравнения (1). Поскольку очевидно, что выражение (6) содержит две произвольные постоянные, то осталось показать, что при любых числовых значениях (7) Учитывая вид общего решения (4) однородного уравнения (2), можно утверждать, что (8) Поскольку по условию теоремы функция (9) С учетом (7), функцию Таким образом, справедливо следующее Правило 2. Для нахождения общего решения неоднородного уравнения (1) достаточно найти любые два линейно независимых решения Согласно высказыванию в теореме 2, это Правило 2 можно более коротко сформулировать следующим образом: общее решение неоднородного уравнения (1) есть сумма общего решения соответствующего однородного уравнения (2) и какого-либо частного решения самого неоднородного уравнения (1): (10) где Замечание 3. Можно показать, что общее решение (6) неоднородного уравнения (1) содержит все решения этого уравнения. Это означает, что любое решение уравнения (1) имеет вид (6) с некоторыми конкретными числовыми значениями произвольных постоянных Как же находить эти три функции
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.12.88 (0.008 с.) |

 ,
,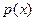 ,
,  и
и  − непрерывные на некотором интервале
− непрерывные на некотором интервале  функции. Эти уравнения занимают видное место среди уравнений 2-го порядка, поскольку, с одной стороны, ими описываются многочисленные реальные процессы и явления практически во всех областях деятельности, а, с другой стороны, точно изучена структура решений таких уравнений, а также известен алгоритм получения этих решений для многих типов таких уравнений. Предполагаемая непрерывность функций
функции. Эти уравнения занимают видное место среди уравнений 2-го порядка, поскольку, с одной стороны, ими описываются многочисленные реальные процессы и явления практически во всех областях деятельности, а, с другой стороны, точно изучена структура решений таких уравнений, а также известен алгоритм получения этих решений для многих типов таких уравнений. Предполагаемая непрерывность функций  ,
,  и
и  .
. , то это уравнение называется однородным линейным дифференциальным уравнением, а иначе неоднородным линейным дифференциальным уравнением.
, то это уравнение называется однородным линейным дифференциальным уравнением, а иначе неоднородным линейным дифференциальным уравнением. .
.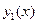 и
и 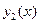 линейно зависимыми на некотором интервале
линейно зависимыми на некотором интервале  значения одной из них получаются из значений другой умножением на одно и то же число:
значения одной из них получаются из значений другой умножением на одно и то же число: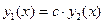
 − некоторое число. В противном случае функции
− некоторое число. В противном случае функции  и
и  , также функции
, также функции  и
и  , если вспомнить, что
, если вспомнить, что  . Приведем важные для дальнейшего изложения примеры линейно независимых функций.
. Приведем важные для дальнейшего изложения примеры линейно независимых функций. и
и  линейно независимы при
линейно независимы при  на любом интервале.
на любом интервале.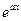
 , т.е.
, т.е.  . По правилу деления степеней с одинаковым основанием получаем, что
. По правилу деления степеней с одинаковым основанием получаем, что  или
или 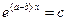 . Поскольку
. Поскольку  , действительно
, действительно  − число!), то экспонента
− число!), то экспонента  при ненулевом показателе степени не может быть равна одному и тому же числу при всех
при ненулевом показателе степени не может быть равна одному и тому же числу при всех  из некоторого интервала. Полученное противоречие и доказывает независимость функций
из некоторого интервала. Полученное противоречие и доказывает независимость функций  и
и  линейно независимы при любом числе
линейно независимы при любом числе  на любом интервале.
на любом интервале.
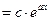 , т.е. (поделив обе части на
, т.е. (поделив обе части на  . Но функция
. Но функция  не является постоянной ни на каком интервале – противоречие.
не является постоянной ни на каком интервале – противоречие. и
и 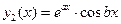 линейно независимы при любом числе
линейно независимы при любом числе  на любом интервале.
на любом интервале.
 , т.е. (поделив на
, т.е. (поделив на 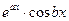 )
)  . Но функция
. Но функция  не является при
не является при 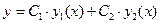 ,
, и
и 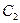 − произвольные постоянные.
− произвольные постоянные.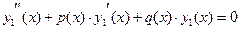 и
и  .
.

 {соберем слагаемые, содержащие
{соберем слагаемые, содержащие 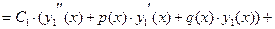
 {учитывая (5)}
{учитывая (5)} 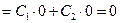 , что и требовалось показать.
, что и требовалось показать. , т.е.
, т.е. 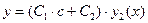 . Поскольку
. Поскольку  тоже будет постоянным (числом). Обозначив это число буквой
тоже будет постоянным (числом). Обозначив это число буквой  , получим, что выражение (4) приобретает вид
, получим, что выражение (4) приобретает вид  , а потому не может из себя представлять общее решение уравнения второго порядка, так как фактически содержит не две, а только одну произвольную постоянную
, а потому не может из себя представлять общее решение уравнения второго порядка, так как фактически содержит не две, а только одну произвольную постоянную  ,
, − какое-либо решение самого уравнения (1) (т.е. его частное решение),
− какое-либо решение самого уравнения (1) (т.е. его частное решение),  функцию:
функцию: .
. .
. .
. в (6) можно представить в виде
в (6) можно представить в виде  . Подставим ее в неоднородное уравнение (1) и убедимся, что оно превратится при этом в верное тождество (а потому действительно функция (6) дает решение уравнения (1) при любых
. Подставим ее в неоднородное уравнение (1) и убедимся, что оно превратится при этом в верное тождество (а потому действительно функция (6) дает решение уравнения (1) при любых 
 {соберем слагаемые, содержащие
{соберем слагаемые, содержащие 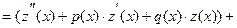
 {учитывая (8) и (9)}
{учитывая (8) и (9)}  , что и требовалось показать.
, что и требовалось показать.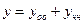 ,
, есть общее решение однородного уравнения (вычисляемое по формуле (4)), а
есть общее решение однородного уравнения (вычисляемое по формуле (4)), а 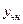 − частное решение неоднородного уравнения.
− частное решение неоднородного уравнения.


