Геометрический смысл определенного интеграла
В примере 1 предыдущего параграфа мы получили такой результат: 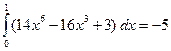 . С другой стороны, в параграфе «Задача о площади криволинейной трапеции» было выяснено (см. формулу (3) там), что значение интеграла . С другой стороны, в параграфе «Задача о площади криволинейной трапеции» было выяснено (см. формулу (3) там), что значение интеграла  выражает собой площадь криволинейной трапеции, изображенной на знакомом уже рисунке. Поэтому, казалось бы, что значение интеграла выражает собой площадь криволинейной трапеции, изображенной на знакомом уже рисунке. Поэтому, казалось бы, что значение интеграла 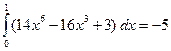 должно выражать собой площадь криволинейной трапеции, ограниченной сверху графиком функции должно выражать собой площадь криволинейной трапеции, ограниченной сверху графиком функции 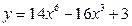 , по бокам отрезками вертикальных прямых, проходящих через числа , по бокам отрезками вертикальных прямых, проходящих через числа 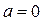 (ось (ось 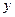 ) и ) и 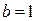 , а снизу − осью , а снизу − осью 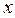 . Но разве площадь может быть отрицательной? Чтобы разобраться в этой ситуации, обратим внимание на то, что на рисунке график функции . Но разве площадь может быть отрицательной? Чтобы разобраться в этой ситуации, обратим внимание на то, что на рисунке график функции 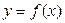 целиком расположен выше оси целиком расположен выше оси 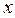 . Только в этом случае образуется фигура того типа, что изображена на рисунке и которая была нами названа криволинейной трапецией. Расположение графика функции . Только в этом случае образуется фигура того типа, что изображена на рисунке и которая была нами названа криволинейной трапецией. Расположение графика функции 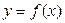 выше оси выше оси 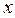 означает (вспомните, как по графику определяются значения функции), что для всех означает (вспомните, как по графику определяются значения функции), что для всех 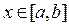 значения этой функции положительны! Но определенный интеграл (по своему определению) не требует от функции такого свойства – значения функции в точках отрезка значения этой функции положительны! Но определенный интеграл (по своему определению) не требует от функции такого свойства – значения функции в точках отрезка 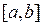 могут быть любого знака (требовалась только непрерывность функции). Поэтому если функция могут быть любого знака (требовалась только непрерывность функции). Поэтому если функция 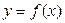 принимает на отрезке принимает на отрезке 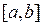 значения разных знаков (а потому ее график частями располагается то выше, то ниже оси значения разных знаков (а потому ее график частями располагается то выше, то ниже оси 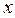 ), то значение интеграла от нее не может выражать площадь того вида криволинейной трапеции, которую мы определяли выше, так как такого типа трапеция просто не вырисовывается. ), то значение интеграла от нее не может выражать площадь того вида криволинейной трапеции, которую мы определяли выше, так как такого типа трапеция просто не вырисовывается.
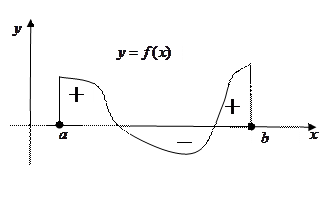 Каков же геометрический смысл числового значения интеграла Каков же геометрический смысл числового значения интеграла  в случае, когда подынтегральная функция в случае, когда подынтегральная функция 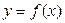 принимает на отрезке принимает на отрезке 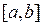 значения разных знаков, а ее график поэтому «ныряет» то под ось значения разных знаков, а ее график поэтому «ныряет» то под ось 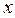 , то «выпрыгивает» над ней? Обратимся к соответствующему рисунку. В случае такого расположения графика функции площадь фигур, расположенных выше оси , то «выпрыгивает» над ней? Обратимся к соответствующему рисунку. В случае такого расположения графика функции площадь фигур, расположенных выше оси 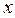 , считается положительной, а площадь фигур, расположенных ниже оси , считается положительной, а площадь фигур, расположенных ниже оси 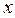 , считается отрицательной (т.е. берется со знаком «−»). Тогда геометрический смысл определенного интеграла , считается отрицательной (т.е. берется со знаком «−»). Тогда геометрический смысл определенного интеграла  состоит в том, что значение интеграла представляет собой алгебраическую сумму указанных выше фигур. Таким образом, если значение интеграла состоит в том, что значение интеграла представляет собой алгебраическую сумму указанных выше фигур. Таким образом, если значение интеграла  оказалось отрицательным, то это означает, что либо весь график функции оказалось отрицательным, то это означает, что либо весь график функции 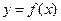 расположен ниже оси расположен ниже оси 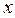 , либо суммарная площадь фигур, расположенных между графиком и осью , либо суммарная площадь фигур, расположенных между графиком и осью 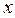 ниже ее, больше суммарной площади аналогичных фигур, расположенных выше оси ниже ее, больше суммарной площади аналогичных фигур, расположенных выше оси 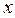 . .
Такой геометрический смысл определенного интеграла позволяет наглядно понять справедливость следующего свойства интегралов по симметричному (относительно нуля) промежутку от четной или нечетной функции. Напомним, что функция 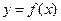 , определенная на отрезке , определенная на отрезке 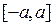 , называется четной (нечетной), если для всех , называется четной (нечетной), если для всех 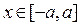 выполнено: выполнено: 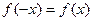 ( ( ). ).
Теорема. Пусть функция 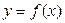 непрерывна на отрезке непрерывна на отрезке 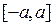 . Тогда . Тогда
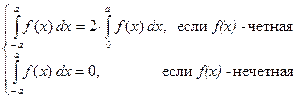 . .
На рисунке слева изображен пример графика четной функции, а справа – нечетной.
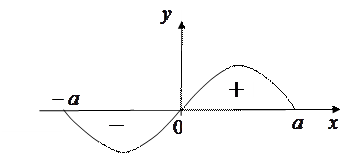 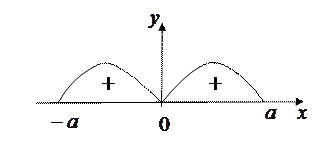
График четной функции симметричен относительно оси  , а потому площади как «положительных» так и «отрицательных» участков слева от оси , а потому площади как «положительных» так и «отрицательных» участков слева от оси 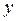 те же самые, что и справа от этой оси. Поэтому алгебраическая сумма всех площадей равна удвоенной алгебраической сумме площадей справа от оси те же самые, что и справа от этой оси. Поэтому алгебраическая сумма всех площадей равна удвоенной алгебраической сумме площадей справа от оси 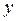 . Изложенный выше геометрический смысл определенного интеграла позволяет теперь убедиться в справедливости верхней строчки в фигурной скобке в формулировке теоремы. График же нечетной функции симметричен относительно начала координат. Поэтому любой «положительный» участок справа от оси . Изложенный выше геометрический смысл определенного интеграла позволяет теперь убедиться в справедливости верхней строчки в фигурной скобке в формулировке теоремы. График же нечетной функции симметричен относительно начала координат. Поэтому любой «положительный» участок справа от оси 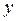 имеет равный ему по площади отрицательный участок. Аналогично о любом «отрицательном» участке справа от оси имеет равный ему по площади отрицательный участок. Аналогично о любом «отрицательном» участке справа от оси 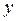 . Поэтому алгебраическая сумма площадей всех участков будет нулевой, что убеждает нас в справедливости и нижней строчки в фигурной скобке в формулировке теоремы. . Поэтому алгебраическая сумма площадей всех участков будет нулевой, что убеждает нас в справедливости и нижней строчки в фигурной скобке в формулировке теоремы.
Рассмотрим пример на применение этой теоремы.
Пример 1. Вычислить 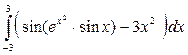 . .
Решение. 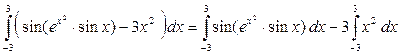 . Покажем, что функция . Покажем, что функция  в первом интеграле нечетна (используя известную нечетность синуса): в первом интеграле нечетна (используя известную нечетность синуса): 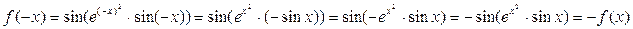 . .
Тогда по изложенной выше теореме интеграл в первом слагаемом равен нулю, а потому 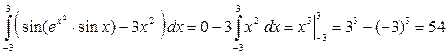 . .
Отметим, что вычислить интеграл 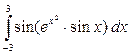 , не опираясь на приведенную теорему, а обычным способом, находя первообразную и применяя формулу Ньютона-Лейбница, принципиально невозможно, так как первообразная для , не опираясь на приведенную теорему, а обычным способом, находя первообразную и применяя формулу Ньютона-Лейбница, принципиально невозможно, так как первообразная для  не выражается через элементарные функции. не выражается через элементарные функции.
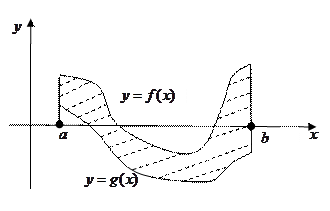 Обобщим теперь формулу для вычисления площади криволинейной трапеции на случай, когда у фигуры две границы (не только верхнее, но и нижнее основание) криволинейны. Пусть фигура на координатной плоскости хОу как на приведенном рисунке ограничена снизу графиком функции Обобщим теперь формулу для вычисления площади криволинейной трапеции на случай, когда у фигуры две границы (не только верхнее, но и нижнее основание) криволинейны. Пусть фигура на координатной плоскости хОу как на приведенном рисунке ограничена снизу графиком функции 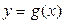 , сверху графиком функции , сверху графиком функции 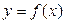 , а по бокам отрезками вертикальных прямых, проходящих через числа а и b на оси х (эти отрезки могут превращаться в точку, если графики сливаются на каком-нибудь конце интервала [ a,b ]). Тогда площадь этой фигуры может быть вычислена по формуле: , а по бокам отрезками вертикальных прямых, проходящих через числа а и b на оси х (эти отрезки могут превращаться в точку, если графики сливаются на каком-нибудь конце интервала [ a,b ]). Тогда площадь этой фигуры может быть вычислена по формуле:
(1) 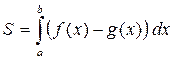 . .
Пример 2. Вычислить площадь фигуры, ограниченной графиками функций 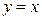 и и 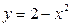 . .
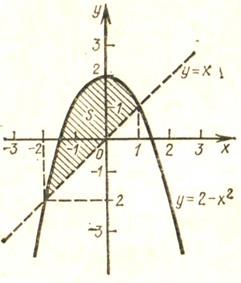 Решение. На рисунке изображен эскиз графиков функций Решение. На рисунке изображен эскиз графиков функций 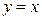 и и 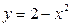 , которые ограничивают фигуру, площадь которой и требуется найти. Для того, чтобы воспользоваться для этой цели формулой (1), необходимо конкретизировать входящие в нее объекты: выражения для функций , которые ограничивают фигуру, площадь которой и требуется найти. Для того, чтобы воспользоваться для этой цели формулой (1), необходимо конкретизировать входящие в нее объекты: выражения для функций 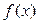 и и 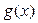 , а также конкретные значения для чисел , а также конкретные значения для чисел  и и 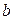 , являющихся пределами интегрирования. В формуле (1) , являющихся пределами интегрирования. В формуле (1) 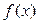 есть выражение для функции, график которой является верхней частью фигуры. Поскольку по рисунку таковым является график функции есть выражение для функции, график которой является верхней частью фигуры. Поскольку по рисунку таковым является график функции 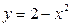 , то , то 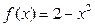 . Аналогично, . Аналогично, 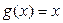 , поскольку график функции , поскольку график функции 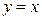 есть нижняя часть фигуры. Числа есть нижняя часть фигуры. Числа  и и 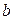 в формуле (1) есть х -координаты (т.е. абсциссы) самой левой и самой правой точки фигуры. Из рисунка видно, что это х -координаты точек пересечения графиков функций в формуле (1) есть х -координаты (т.е. абсциссы) самой левой и самой правой точки фигуры. Из рисунка видно, что это х -координаты точек пересечения графиков функций 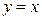 и и 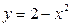 . Как известно, для их получения нужно приравнять правые части этих функций и решить полученное уравнение: . Как известно, для их получения нужно приравнять правые части этих функций и решить полученное уравнение:  , , 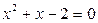 , , 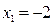 и и 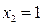 . Отсюда следует, что для нашего примера . Отсюда следует, что для нашего примера  и и 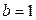 . Поскольку все параметры для формулы (1) определены, считаем по ней искомую площадь: . Поскольку все параметры для формулы (1) определены, считаем по ней искомую площадь:
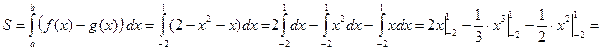 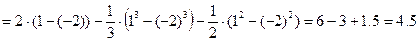 . .
Итак, площадь 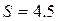 квадратных единиц. квадратных единиц.
Пример 3. Найти площадь фигуры, ограниченной графиками 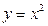 и и 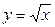 . .
 Решение. Эскиз графиков функций Решение. Эскиз графиков функций 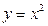 и и 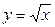 изображен на рисунке и определяет искомую фигуру. Из этого рисунка видно, что в данном примере формула (1) должна использоваться со следующими параметрами: изображен на рисунке и определяет искомую фигуру. Из этого рисунка видно, что в данном примере формула (1) должна использоваться со следующими параметрами: 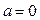 , , 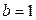 , , 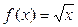 и и  . Поэтому получаем по формуле (1): . Поэтому получаем по формуле (1):
  . .
Итак, искомая площадь 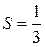 квадратной единицы. квадратной единицы.
|



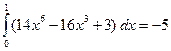 . С другой стороны, в параграфе «Задача о площади криволинейной трапеции» было выяснено (см. формулу (3) там), что значение интеграла
. С другой стороны, в параграфе «Задача о площади криволинейной трапеции» было выяснено (см. формулу (3) там), что значение интеграла  выражает собой площадь криволинейной трапеции, изображенной на знакомом уже рисунке. Поэтому, казалось бы, что значение интеграла
выражает собой площадь криволинейной трапеции, изображенной на знакомом уже рисунке. Поэтому, казалось бы, что значение интеграла 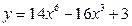 , по бокам отрезками вертикальных прямых, проходящих через числа
, по бокам отрезками вертикальных прямых, проходящих через числа 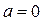 (ось
(ось 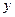 ) и
) и 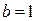 , а снизу − осью
, а снизу − осью 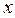 . Но разве площадь может быть отрицательной? Чтобы разобраться в этой ситуации, обратим внимание на то, что на рисунке график функции
. Но разве площадь может быть отрицательной? Чтобы разобраться в этой ситуации, обратим внимание на то, что на рисунке график функции 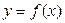 целиком расположен выше оси
целиком расположен выше оси 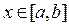 значения этой функции положительны! Но определенный интеграл (по своему определению) не требует от функции такого свойства – значения функции в точках отрезка
значения этой функции положительны! Но определенный интеграл (по своему определению) не требует от функции такого свойства – значения функции в точках отрезка 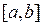 могут быть любого знака (требовалась только непрерывность функции). Поэтому если функция
могут быть любого знака (требовалась только непрерывность функции). Поэтому если функция  Каков же геометрический смысл числового значения интеграла
Каков же геометрический смысл числового значения интеграла 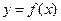 расположен ниже оси
расположен ниже оси 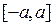 , называется четной (нечетной), если для всех
, называется четной (нечетной), если для всех 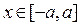 выполнено:
выполнено: 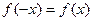 (
( ).
).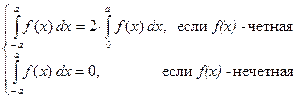 .
.

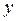 , а потому площади как «положительных» так и «отрицательных» участков слева от оси
, а потому площади как «положительных» так и «отрицательных» участков слева от оси 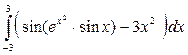 .
.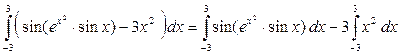 . Покажем, что функция
. Покажем, что функция  в первом интеграле нечетна (используя известную нечетность синуса):
в первом интеграле нечетна (используя известную нечетность синуса): 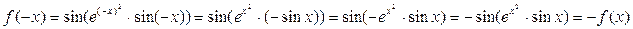 .
.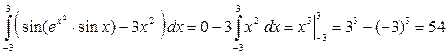 .
.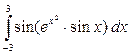 , не опираясь на приведенную теорему, а обычным способом, находя первообразную и применяя формулу Ньютона-Лейбница, принципиально невозможно, так как первообразная для
, не опираясь на приведенную теорему, а обычным способом, находя первообразную и применяя формулу Ньютона-Лейбница, принципиально невозможно, так как первообразная для  Обобщим теперь формулу для вычисления площади криволинейной трапеции на случай, когда у фигуры две границы (не только верхнее, но и нижнее основание) криволинейны. Пусть фигура на координатной плоскости хОу как на приведенном рисунке ограничена снизу графиком функции
Обобщим теперь формулу для вычисления площади криволинейной трапеции на случай, когда у фигуры две границы (не только верхнее, но и нижнее основание) криволинейны. Пусть фигура на координатной плоскости хОу как на приведенном рисунке ограничена снизу графиком функции 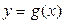 , сверху графиком функции
, сверху графиком функции 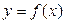 , а по бокам отрезками вертикальных прямых, проходящих через числа а и b на оси х (эти отрезки могут превращаться в точку, если графики сливаются на каком-нибудь конце интервала [ a,b ]). Тогда площадь этой фигуры может быть вычислена по формуле:
, а по бокам отрезками вертикальных прямых, проходящих через числа а и b на оси х (эти отрезки могут превращаться в точку, если графики сливаются на каком-нибудь конце интервала [ a,b ]). Тогда площадь этой фигуры может быть вычислена по формуле: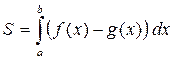 .
.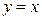 и
и 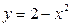 .
. Решение. На рисунке изображен эскиз графиков функций
Решение. На рисунке изображен эскиз графиков функций 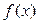 и
и 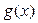 , а также конкретные значения для чисел
, а также конкретные значения для чисел  и
и 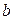 , являющихся пределами интегрирования. В формуле (1)
, являющихся пределами интегрирования. В формуле (1) 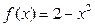 . Аналогично,
. Аналогично, 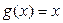 , поскольку график функции
, поскольку график функции  ,
, 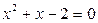 ,
, 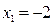 и
и 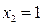 . Отсюда следует, что для нашего примера
. Отсюда следует, что для нашего примера  и
и 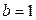 . Поскольку все параметры для формулы (1) определены, считаем по ней искомую площадь:
. Поскольку все параметры для формулы (1) определены, считаем по ней искомую площадь: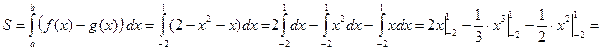
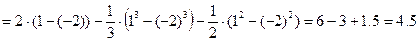 .
.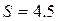 квадратных единиц.
квадратных единиц.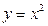 и
и 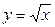 .
. Решение. Эскиз графиков функций
Решение. Эскиз графиков функций 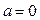 ,
, 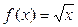 и
и  . Поэтому получаем по формуле (1):
. Поэтому получаем по формуле (1):
 .
.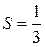 квадратной единицы.
квадратной единицы.


