Уравнения, допускающие понижение порядка
Одним из методов решения уравнений второго порядка является сведение его к последовательности уравнений первого порядка (если это, конечно, возможно). Итак, снова рассмотрим уравнение второго порядка вида
(1)  . .
Оказывается, что если формула в правой части (1) не содержит некоторых своих переменных, то в ряде случаев такое уравнение может быть сведено к последовательному решению уравнений 1-го порядка. Рассмотрим эти случаи.
1. Уравнения, не содержащие  и и  . Пусть уравнение (1) в правой части не содержит . Пусть уравнение (1) в правой части не содержит  и и  , т.е. является уравнением вида , т.е. является уравнением вида
(2)  . .
Это самый простой вид уравнения второго порядка, так как требует восстановить функцию по известной ее второй производной. Такого типа уравнение (уравнение  ) мы решили в предыдущем параграфе, последовательным интегрированием находя сначала выражение для первой производной ) мы решили в предыдущем параграфе, последовательным интегрированием находя сначала выражение для первой производной  искомого решения, а затем и для самого решения искомого решения, а затем и для самого решения  . По этой же схеме решается и любое другое уравнение вида (2): вычисляя неопределенный интеграл от его правой части . По этой же схеме решается и любое другое уравнение вида (2): вычисляя неопределенный интеграл от его правой части 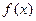 находят выражение для первой производной находят выражение для первой производной  , а повторным интегрированием полученного выражения находят вид общего решения уравнения (2). , а повторным интегрированием полученного выражения находят вид общего решения уравнения (2).
Пример 1. Найти общее решение уравнения  . .
Решение. Это уравнение не содержит искомой функции  и ее производной и ее производной  . Деля обе части уравнения на . Деля обе части уравнения на  , приведем его к виду (2): , приведем его к виду (2):  . Согласно предложенной выше схеме решения таких уравнений интегрированием его правой части находим сначала выражение для . Согласно предложенной выше схеме решения таких уравнений интегрированием его правой части находим сначала выражение для  : : 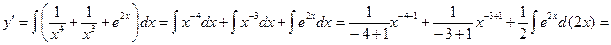 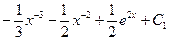 . Таким образом, мы нашли выражение для производной искомого решения: . Таким образом, мы нашли выражение для производной искомого решения:  . Повторным интегрированием правой части находим выражение для самого решения: . Повторным интегрированием правой части находим выражение для самого решения:  = =  . Таким образом, общее решение исходного уравнения имеет вид . Таким образом, общее решение исходного уравнения имеет вид  , где , где  и и 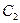 − произвольные постоянные. − произвольные постоянные.
2. Уравнения, не содержащие  . Пусть уравнение (1) в правой части не содержит искомую функцию . Пусть уравнение (1) в правой части не содержит искомую функцию  , т.е. является уравнением вида , т.е. является уравнением вида
(3)  . .
Найдем сначала вспомогательную функцию  такую, которая является производной от искомой функции такую, которая является производной от искомой функции  : :  . Тогда вторая производная от решения окажется равной первой производной от . Тогда вторая производная от решения окажется равной первой производной от  , так как , так как  . Подставляя . Подставляя  и и  в (3), получим, что если в (3), получим, что если  является решением (3), то вспомогательная функция является решением (3), то вспомогательная функция  должна быть решением уравнения должна быть решением уравнения
(4)  . .
Уравнение (4) – это уже уравнение 1-го порядка для нахождения функции  , которое в некоторых случаях может быть решено методами, разобранными нами для решения уравнений первого порядка. Допустим, что мы одним их этих методов получили общее решение уравнения (4) в виде , которое в некоторых случаях может быть решено методами, разобранными нами для решения уравнений первого порядка. Допустим, что мы одним их этих методов получили общее решение уравнения (4) в виде  . Вспоминая, что . Вспоминая, что  , получаем выражение для производной искомого решения: , получаем выражение для производной искомого решения:  . Как мы не раз уже делали, восстанавливаем функцию по ее производной с помощью интегрирования: . Как мы не раз уже делали, восстанавливаем функцию по ее производной с помощью интегрирования:
(5) 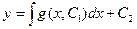 . .
Выражение (5) является общим решением уравнения (3), в котором постоянная интегрирования 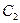 выписана явно, а потому при вычислении интеграла выписана явно, а потому при вычислении интеграла 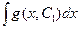 в (5) оставляем только одну первообразную (т.е. без «+С»). в (5) оставляем только одну первообразную (т.е. без «+С»).
Пример 2. Найти решение задачи Коши  . .
Решение. В этом примере необходимо найти такое решение  уравнения уравнения
(6)  , ,
которое при  принимает значение принимает значение  , производная , производная  которого при которого при  принимает значение принимает значение  . Найдем сначала все решения уравнения (6), а затем выберем из них нужное. Это уравнение не содержит искомой функции . Найдем сначала все решения уравнения (6), а затем выберем из них нужное. Это уравнение не содержит искомой функции  . Согласно предложенному выше плану решения таких уравнений найдем сначала выражение для функции, являющейся производной . Согласно предложенному выше плану решения таких уравнений найдем сначала выражение для функции, являющейся производной  искомого решения, которую обозначим искомого решения, которую обозначим  : :  . Тогда . Тогда  . Подставляя . Подставляя  и и  в (6), получим, что вспомогательная функция в (6), получим, что вспомогательная функция  должна быть решением уравнения должна быть решением уравнения
(7)  . .
Разрешая это уравнение (оно уже первого порядка) относительно производной  , получим уравнение , получим уравнение
(8)  . .
Это уравнение с разделяющимися переменными, так как его правая часть 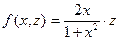 представляется в виде произведения двух функций представляется в виде произведения двух функций 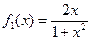 и и  , каждая из которых зависит только от одной переменной , каждая из которых зависит только от одной переменной  и и 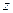 соответственно. Поэтому далее действуем по схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (после уравнения (6) там): соответственно. Поэтому далее действуем по схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (после уравнения (6) там):
1. Умножаем обе части (8) на  : :  . .
2. Делим обе части полученного уравнения на 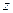 , в результате чего получаем уравнение с разделенными переменными , в результате чего получаем уравнение с разделенными переменными  . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 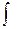 перед правой и левой частью уравнения: перед правой и левой частью уравнения:  . .
2) Вычисляя полученные интегралы: а)  (табличный интеграл; «+С» в этом интеграле не пишем), б) (табличный интеграл; «+С» в этом интеграле не пишем), б)  {вносим {вносим 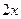 под знак дифференциала, поправочный множитель при этом не нужен, так как под знак дифференциала, поправочный множитель при этом не нужен, так как  }= }=  {получается табличный интеграл вида {получается табличный интеграл вида  при при 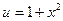 }= }=  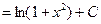 (модуль под знаком логарифма опущен, так как выражение (модуль под знаком логарифма опущен, так как выражение  положительно для всех значений положительно для всех значений  ). Таким образом, ). Таким образом,
получаем следующий общий интеграл уравнения (8):
(9)  . .
3) Получим из общего интеграла (9) общее решение уравнения (8). По лемме в параграфе «Уравнение с разделяющимися переменными» общий интеграл вида  дает общее решение дает общее решение  , где , где  − произвольная постоянная, не равная 0 ( − произвольная постоянная, не равная 0 (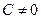 ). Тогда из (9) получаем, что общее решение уравнения (8) имеет вид ). Тогда из (9) получаем, что общее решение уравнения (8) имеет вид  . Учитывая свойство логарифмов . Учитывая свойство логарифмов  , получаем общее решение в виде , получаем общее решение в виде
(10)  , ,
где  может принимать любое значение, кроме может принимать любое значение, кроме  . .
4. Поскольку в пункте 2 мы делили обе части уравнения на 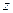 , то потеряли решение , то потеряли решение  уравнения (8). Учитывая, что уравнения (8). Учитывая, что  получается в (10) как раз при получается в (10) как раз при  , то выражение (10) содержит (при различных значениях , то выражение (10) содержит (при различных значениях  ) все решения уравнения (8), но теперь произвольной постоянной ) все решения уравнения (8), но теперь произвольной постоянной  будут позволены все числовые значения (и будут позволены все числовые значения (и  тоже!). тоже!).
Заменим в (10) обозначение произвольной постоянной с  на на  , поскольку далее у нас появится еще одна произвольная постоянная, которую мы обозначим , поскольку далее у нас появится еще одна произвольная постоянная, которую мы обозначим 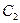 . Таким образом, все решения уравнения (8) содержаться в формуле . Таким образом, все решения уравнения (8) содержаться в формуле
(11)  , ,
где произвольная постоянная  может пробегать любые числовые значения. может пробегать любые числовые значения.
Вспоминая, что решения исходного уравнения (6) удовлетворяют условию  , то из (11) получаем для искомой функции , то из (11) получаем для искомой функции  уравнение уравнение
(12)  . .
Вспоминая, что по известному выражению для производной сама функция восстанавливается вычислением неопределенного интеграла, получаем  . Таким образом, общее решение уравнения (6) имеет вид . Таким образом, общее решение уравнения (6) имеет вид
(13)  . .
Для решения исходной задачи Коши осталось определить конкретные значения произвольных постоянных  и и 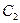 из условий из условий 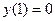 и и  . Подставляя . Подставляя  в (13) и (12), получаем из условий в (13) и (12), получаем из условий 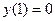 и и  следующую систему для определения следующую систему для определения  и и 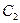 : :
(14)  . .
Из второго уравнения системы сразу получаем  . Подставляя это значение . Подставляя это значение  в первое уравнение системы (14), находим и в первое уравнение системы (14), находим и 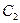 : :  . Подставляя эти значения . Подставляя эти значения  и и  в (13), получаем окончательное решение исходной задачи Коши: в (13), получаем окончательное решение исходной задачи Коши:  . .
3. Уравнения, не содержащие независимой переменной  . Это наиболее сложный случай по сравнению с разобранными выше. Пусть уравнение (1) в правой части не содержит независимую переменную . Это наиболее сложный случай по сравнению с разобранными выше. Пусть уравнение (1) в правой части не содержит независимую переменную  , т.е. является уравнением вида , т.е. является уравнением вида
(15)  . .
Найдем сначала такую вспомогательную функцию  от переменной от переменной  , чтобы для любого решения , чтобы для любого решения  уравнения (15) выполнялось такое тождество: уравнения (15) выполнялось такое тождество:
(16)  . .
Выясним теперь, какому дифференциальному уравнения должна удовлетворять функция с таким свойством  . Итак, пусть . Итак, пусть  есть решение уравнения (15), т.е выполнено такое тождество по переменной есть решение уравнения (15), т.е выполнено такое тождество по переменной  : :
(17) 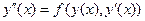 . .
Далее, пусть функция  такова, что выполнено тождество (16). Возьмем производную от правой и левой части в тождестве (16) (учитывая для производной в правой части формулу для производной сложной функции): такова, что выполнено тождество (16). Возьмем производную от правой и левой части в тождестве (16) (учитывая для производной в правой части формулу для производной сложной функции):
(18) 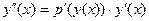 . .
Левые части тождеств (17) и (18) равны, следовательно, должны быть равны и правые части, т.е. должно выполняться тождество:
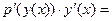  . .
Заменив, согласно (16), в этом тождестве  на на  , получим, что должно выполняться тождество: , получим, что должно выполняться тождество:
(19)   . .
Для того, чтобы обеспечить выполнение (19), достаточно найти такую функцию  , для которой бы для всех , для которой бы для всех  выполнялось бы тождество: выполнялось бы тождество:
(20) 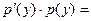  . .
Соотношение (20) является дифференциальным уравнением уже 1-го порядка относительно вспомогательной функции  . Опуская в уравнении (20), как обычно, для краткости аргумент . Опуская в уравнении (20), как обычно, для краткости аргумент  искомой функции, получаем следующее уравнение: искомой функции, получаем следующее уравнение:
(21)   . .
Допустим, что мы нашли общее решение этого уравнения:
(22)  , ,
где  произвольная постоянная, появляющаяся при поиске общего решения уравнения 1-го порядка (21). Тогда, согласно (16) и (22), решение исходного уравнения (15) удовлетворяет тождеству произвольная постоянная, появляющаяся при поиске общего решения уравнения 1-го порядка (21). Тогда, согласно (16) и (22), решение исходного уравнения (15) удовлетворяет тождеству  , т.е. является решением еще одного уравнения 1-го порядка: , т.е. является решением еще одного уравнения 1-го порядка:
(23)  . .
Таким образом, поиск решения уравнения 2-го порядка вида (15) сводится к решению двух уравнений 1-го порядка: сначала ищется общее решение (22) уравнения (21) относительно функции  , а затем ищется решение уравнения (23) относительно искомой функции , а затем ищется решение уравнения (23) относительно искомой функции  . Заметим, что уравнение (21) получается из исходного уравнения (15) заменой . Заметим, что уравнение (21) получается из исходного уравнения (15) заменой 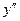 в левой части на в левой части на  , а , а  в правой части – на в правой части – на 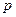 . .
Пример 3. Найти решение уравнения  . .
Решение. Сначала приведем уравнение к виду (15), разделив обе его части на  : :
(24)  . .
Заметим, что, деля обе части уравнения на  , мы теряем решение , мы теряем решение  , которое потом обязательно учтем. То, что функция , которое потом обязательно учтем. То, что функция  является решением исходного уравнения, проверяется непосредственной подстановкой ее в само уравнение. Уравнение второго порядка (24) не содержит независимой переменной является решением исходного уравнения, проверяется непосредственной подстановкой ее в само уравнение. Уравнение второго порядка (24) не содержит независимой переменной  . Поэтому по предложенной выше схеме сначала ищем такую вспомогательную функцию . Поэтому по предложенной выше схеме сначала ищем такую вспомогательную функцию  от переменной от переменной  , чтобы для любого решения , чтобы для любого решения  уравнения (24) выполнялось такое тождество уравнения (24) выполнялось такое тождество  . Как сказано выше, уравнение для . Как сказано выше, уравнение для  получается из уравнения (24) заменой получается из уравнения (24) заменой 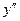 в левой части на в левой части на  , а , а  в правой части – на в правой части – на 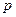 : :
(25)  . .
Решим это уравнение относительно функции  . Перенося все в левую часть и вынося . Перенося все в левую часть и вынося 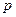 за скобку, получим: за скобку, получим:  . Видно, что одно из решений этого уравнения: . Видно, что одно из решений этого уравнения:
(26) 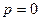 . .
Другие решения уравнения (25) есть решения уравнения
(27)  . .
Решим уравнение (27). Это уравнение с разделяющимися переменными, так как его правую часть можно представить в виде произведения двух функций, зависящих порознь от одной из переменных: 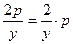 . Поэтому действуем по привычной схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (с учетом, что независимая переменная теперь обозначена не . Поэтому действуем по привычной схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (с учетом, что независимая переменная теперь обозначена не  , а , а  , а искомая функция , а искомая функция 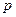 , а не , а не  : :
1. Умножаем обе части (27) на  : :  . .
2. Делим обе части полученного уравнения на 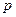 , в результате чего получаем уравнение с разделенными переменными , в результате чего получаем уравнение с разделенными переменными 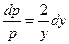 . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 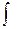 перед правой и левой частью уравнения: перед правой и левой частью уравнения:
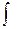 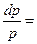 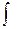 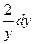 . .
2) Вычисляя полученные интегралы: а) 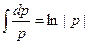 (табличный интеграл; «+С» в этом интеграле не пишем), б) (табличный интеграл; «+С» в этом интеграле не пишем), б)  ={с учетом свойств логарифма: ={с учетом свойств логарифма:  }= }=  Таким образом, получаем следующий общий интеграл уравнения (27): Таким образом, получаем следующий общий интеграл уравнения (27):
(28)  . .
3) Получим из общего интеграла (28) общее решение уравнения (27). По лемме в параграфе «Уравнение с разделяющимися переменными» общий интеграл вида 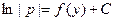 дает общее решение дает общее решение 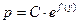 , где , где  − произвольная постоянная, не равная 0 ( − произвольная постоянная, не равная 0 (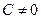 ). Тогда из (28) получаем, что общее решение уравнения (27) имеет вид ). Тогда из (28) получаем, что общее решение уравнения (27) имеет вид  . Учитывая свойство логарифмов . Учитывая свойство логарифмов  , получаем общее решение в виде , получаем общее решение в виде
(29)  , ,
где  может принимать любое значение, кроме может принимать любое значение, кроме  . .
4. Поскольку в пункте 2 мы делили обе части уравнения на 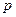 , то потеряли решение , то потеряли решение 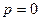 уравнения (27). Учитывая, что уравнения (27). Учитывая, что 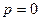 получается из (29) как раз при получается из (29) как раз при  , то выражение (29) содержит (при различных значениях , то выражение (29) содержит (при различных значениях  ) все решения уравнения (27), но теперь произвольной постоянной ) все решения уравнения (27), но теперь произвольной постоянной  будут позволены все числовые значения (и будут позволены все числовые значения (и  ). Отметим, что при ). Отметим, что при  получим и отмеченное выше решение (26) уравнения (25). Таким образом, выражение (29) дает общее решение уравнения (25) при всевозможных значениях произвольной постоянной С. получим и отмеченное выше решение (26) уравнения (25). Таким образом, выражение (29) дает общее решение уравнения (25) при всевозможных значениях произвольной постоянной С.
Заменим в (29) обозначение произвольной постоянной с  на на  , поскольку далее у нас снова появится еще одна произвольная постоянная, которую мы обозначим , поскольку далее у нас снова появится еще одна произвольная постоянная, которую мы обозначим 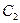 . Таким образом, все решения уравнения (25) содержаться в формуле . Таким образом, все решения уравнения (25) содержаться в формуле
(30)  , ,
где произвольная постоянная  может пробегать любые числовые значения. может пробегать любые числовые значения.
Далее, согласно схеме решений уравнения такого типа, осталось решить уравнение вида (23), где, согласно (30),  . Получаем уравнение на искомую функцию . Получаем уравнение на искомую функцию  : :
(31)  . .
Уравнение (31) − это снова уравнение с разделяющимися переменными, решаемое по известной схеме:
1. Умножаем обе части (27) на  : :  . .
2. Делим обе части полученного уравнения на  , в результате чего получаем уравнение с разделенными переменными , в результате чего получаем уравнение с разделенными переменными 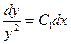 . .
3. Решаем полученное уравнение по схеме решения уравнения с разделенными переменными.
1) Навешиваем значок 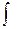 перед правой и левой частью уравнения: перед правой и левой частью уравнения:
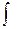  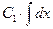 . .
2) Вычисляя полученные интегралы: а)  («+С» не пишем), б) («+С» не пишем), б) 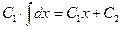 . Таким образом, получаем следующий общий интеграл уравнения (31): . Таким образом, получаем следующий общий интеграл уравнения (31):
(32)  . .
3) «Переворачивая» обе части в (32) и умножая их на 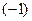 , получим из общего интеграла (32) общее решение уравнения (31): , получим из общего интеграла (32) общее решение уравнения (31):
(33) 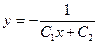 , ,
где  и и 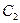 могут принимать любые значения (только одновременно не обращаться в могут принимать любые значения (только одновременно не обращаться в  , чтобы формула (33) имела смысл). , чтобы формула (33) имела смысл).
4. Поскольку в пункте 2 мы делили обе части уравнения на  , то потеряли решение , то потеряли решение  уравнения (31). Это решение мы заметили еще в самом начале, после получения уравнения (24). уравнения (31). Это решение мы заметили еще в самом начале, после получения уравнения (24).
Итак, решением исходного уравнения  являются функции являются функции 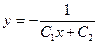 (при любых значениях (при любых значениях  и и 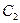 , одновременно не обращающимся в , одновременно не обращающимся в  ) и функция ) и функция  . .
|



 .
. и
и  . Пусть уравнение (1) в правой части не содержит
. Пусть уравнение (1) в правой части не содержит  .
. ) мы решили в предыдущем параграфе, последовательным интегрированием находя сначала выражение для первой производной
) мы решили в предыдущем параграфе, последовательным интегрированием находя сначала выражение для первой производной 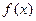 находят выражение для первой производной
находят выражение для первой производной  .
. , приведем его к виду (2):
, приведем его к виду (2):  . Согласно предложенной выше схеме решения таких уравнений интегрированием его правой части находим сначала выражение для
. Согласно предложенной выше схеме решения таких уравнений интегрированием его правой части находим сначала выражение для 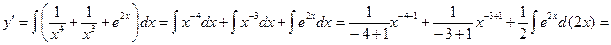
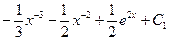 . Таким образом, мы нашли выражение для производной искомого решения:
. Таким образом, мы нашли выражение для производной искомого решения:  . Повторным интегрированием правой части находим выражение для самого решения:
. Повторным интегрированием правой части находим выражение для самого решения:  =
=  . Таким образом, общее решение исходного уравнения имеет вид
. Таким образом, общее решение исходного уравнения имеет вид  , где
, где  и
и 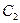 − произвольные постоянные.
− произвольные постоянные. .
. такую, которая является производной от искомой функции
такую, которая является производной от искомой функции  :
:  . Тогда вторая производная от решения окажется равной первой производной от
. Тогда вторая производная от решения окажется равной первой производной от  . Подставляя
. Подставляя  и
и  в (3), получим, что если
в (3), получим, что если  .
. . Вспоминая, что
. Вспоминая, что  . Как мы не раз уже делали, восстанавливаем функцию по ее производной с помощью интегрирования:
. Как мы не раз уже делали, восстанавливаем функцию по ее производной с помощью интегрирования: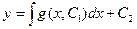 .
.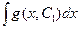 в (5) оставляем только одну первообразную (т.е. без «+С»).
в (5) оставляем только одну первообразную (т.е. без «+С»). .
. ,
, принимает значение
принимает значение  , производная
, производная  которого при
которого при  . Найдем сначала все решения уравнения (6), а затем выберем из них нужное. Это уравнение не содержит искомой функции
. Найдем сначала все решения уравнения (6), а затем выберем из них нужное. Это уравнение не содержит искомой функции  . Тогда
. Тогда  . Подставляя
. Подставляя  .
. , получим уравнение
, получим уравнение .
.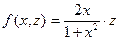 представляется в виде произведения двух функций
представляется в виде произведения двух функций 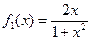 и
и  , каждая из которых зависит только от одной переменной
, каждая из которых зависит только от одной переменной  и
и 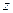 соответственно. Поэтому далее действуем по схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (после уравнения (6) там):
соответственно. Поэтому далее действуем по схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (после уравнения (6) там): :
:  .
. .
.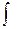 перед правой и левой частью уравнения:
перед правой и левой частью уравнения:  .
. (табличный интеграл; «+С» в этом интеграле не пишем), б)
(табличный интеграл; «+С» в этом интеграле не пишем), б)  {вносим
{вносим 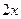 под знак дифференциала, поправочный множитель при этом не нужен, так как
под знак дифференциала, поправочный множитель при этом не нужен, так как  }=
}=  {получается табличный интеграл вида
{получается табличный интеграл вида  при
при 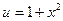 }=
}= 
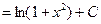 (модуль под знаком логарифма опущен, так как выражение
(модуль под знаком логарифма опущен, так как выражение  положительно для всех значений
положительно для всех значений  .
. дает общее решение
дает общее решение  , где
, где  − произвольная постоянная, не равная 0 (
− произвольная постоянная, не равная 0 (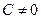 ). Тогда из (9) получаем, что общее решение уравнения (8) имеет вид
). Тогда из (9) получаем, что общее решение уравнения (8) имеет вид  . Учитывая свойство логарифмов
. Учитывая свойство логарифмов  , получаем общее решение в виде
, получаем общее решение в виде ,
, .
. уравнения (8). Учитывая, что
уравнения (8). Учитывая, что  ,
, .
. . Таким образом, общее решение уравнения (6) имеет вид
. Таким образом, общее решение уравнения (6) имеет вид .
.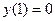 и
и  . Подставляя
. Подставляя  .
. . Подставляя это значение
. Подставляя это значение  . Подставляя эти значения
. Подставляя эти значения  .
. .
. от переменной
от переменной  .
.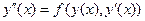 .
.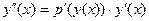 .
.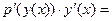
 .
. , получим, что должно выполняться тождество:
, получим, что должно выполняться тождество:
 .
.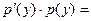
 .
.
 .
. ,
, , т.е. является решением еще одного уравнения 1-го порядка:
, т.е. является решением еще одного уравнения 1-го порядка: .
.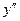 в левой части на
в левой части на  , а
, а 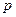 .
. .
. .
. .
. . Видно, что одно из решений этого уравнения:
. Видно, что одно из решений этого уравнения: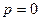 .
. .
.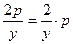 . Поэтому действуем по привычной схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (с учетом, что независимая переменная теперь обозначена не
. Поэтому действуем по привычной схеме решения таких уравнений, приведенной в параграфе «Уравнение с разделяющимися переменными» (с учетом, что независимая переменная теперь обозначена не  :
:  .
.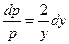 .
.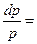
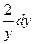 .
.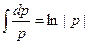 (табличный интеграл; «+С» в этом интеграле не пишем), б)
(табличный интеграл; «+С» в этом интеграле не пишем), б)  ={с учетом свойств логарифма:
={с учетом свойств логарифма:  }=
}=  Таким образом, получаем следующий общий интеграл уравнения (27):
Таким образом, получаем следующий общий интеграл уравнения (27): .
.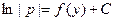 дает общее решение
дает общее решение 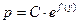 , где
, где  . Учитывая свойство логарифмов
. Учитывая свойство логарифмов  ,
, ,
, . Получаем уравнение на искомую функцию
. Получаем уравнение на искомую функцию  .
. .
. , в результате чего получаем уравнение с разделенными переменными
, в результате чего получаем уравнение с разделенными переменными 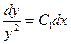 .
.
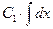 .
. («+С» не пишем), б)
(«+С» не пишем), б) 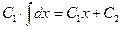 . Таким образом, получаем следующий общий интеграл уравнения (31):
. Таким образом, получаем следующий общий интеграл уравнения (31): .
.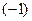 , получим из общего интеграла (32) общее решение уравнения (31):
, получим из общего интеграла (32) общее решение уравнения (31):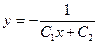 ,
, , чтобы формула (33) имела смысл).
, чтобы формула (33) имела смысл). уравнения (31). Это решение мы заметили еще в самом начале, после получения уравнения (24).
уравнения (31). Это решение мы заметили еще в самом начале, после получения уравнения (24).


