
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные методы интегрированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 7.4.1. Непосредственное интегрирование Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме. Пример. Найти интегралы: 1) Решение. На основании свойств 3 и 4 неопределенного интеграла и таблицы интегралов имеем
2) Решение. Воспользуемся свойствами 3 и 4 неопределенного интеграла:
3) 7.4.2. Метод подстановки (замена переменной) Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных. Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: 1)
2)
Пример. Найти интегралы, используя подходящую подстановку:
1) Решение. Введем подстановку t = x 3+5. Тогда dt = d (x 3+5); dt =3 x 2 dx. Отсюда x 2 dx = dt /3. Таким образом,
Ответ должен быть выражен через «старую» переменную х. Подставляя в результат интегрирования t = x 3+5. Окончательно получим
2) Решение.
Условимся в дальнейшем все промежуточные рассуждения и выкладки заключать в вертикальные скобки (как было сделано в примере 2).
7.4.3. Интегрирование по частям Интегрированием по частям называется нахождение интеграла по формуле
где u и v непрерывно дифференцируемые функции от х. С помощью формулы (6.4.1) нахождение интеграла При этом в качестве u берется функция, которая при дифференцировании упрощается, а в качестве dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден. Пример. При нахождении интеграла
Примеры №1. Найти интегралы непосредственным интегрированием: а) б) в) г) Решение. а) Почленно поделив числитель подынтегральной дроби на знаменатель, будем иметь
Тогда б) Воспользуемся свойствами 3 и 4 неопределенного интеграла, тем самым сводя исходный интеграл к сумме табличных интегралов:
в)
г) Здесь мы воспользовались свойством 5 неопределенного интеграла и формулой 4 пункта 7.3.
№2. Найти интегралыметодом подстановки: а) б) в) г) Решение. а) б) в) г)
№3. Найти интегралы с помощью метода интегрирования по частям: а) б) Решение. а) Положим
б) К последнему интегралу снова применим формулу интегрирования по частям. Положим
Подставляя найденное выражение в соотношение (*), получим
Варианты заданий №7.1. Найти интегралы непосредственным интегрированием: а) б) в) г) д) е) ж) з) и) к) л) м)
№7.2. Найти интегралы методом подстановки: а) б) в) г) д) е) ж) з) и) к) л) м) №7.3. Найти интегралы с помощью метода интегрирования по частям: а) б) в) г) д) е) ж) з) и) к) 7.7. Контрольные вопросы
1. Что такое первообразная? Обладают ли первообразные одной функции свойством единственности? 2. Дайте определение, в том числе виде математического выражения, неопределенного интеграла. 3. Что такое подынтегральная функция? Подынтегральное выражение? 4. Перечислите основные свойства неопределенного интеграла. Запишите эти свойства в виде математических выражений. 5. Воспроизведите таблицу основных интегралов. Докажите справедливость записанных выражений с использованием операции дифференцирования. 6. В чем заключается метод замены переменной в определенном интеграле? метод интегрирования по частям? 7. Какие функции в подынтегральном выражении рекомендуется выбирать в качестве и и dv при интегрировании по частям? 8. Назовите основные типы интегралов, к которым применяется метод интегрирования по частям. 9. Что называется рациональной дробью? Как выделить из неправильной рациональной дроби и правильную дробь? Как разложить правильную дробь на сумму простейших?
Глава 8. Определенный интеграл Основные понятия и свойства определенного интеграла Пусть функция f (x) определена на отрезке [ a; b ]. Разобьем отрезок [ a; b ] на n частей точками a=x 0 <x 1 <…<xn– 1 <x n =b; на каждом элементарном отрезке [ xk– 1, xk ] выберем произвольную точку ck и обозначим через
Интегральной сумм ой для функции f (x) на отрезке [ a; b ] называется сумма вида
Определенным интегралом от функции f (x) на отрезке [ a; b ] называется предел интегральной суммы (7.1.1), при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
При этом f (x) называется подынтегральной функцией, x – переменной интегрирования, числа а и b – соответственно нижним и верхним пределами интегрирования, [ a; b ] – промежутком интегрирования.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

 .
.
 .
.
 .
. , где t – новая переменная, а φ (t) – функция, имеющая непрерывную производную. Тогда формула замены переменной
, где t – новая переменная, а φ (t) – функция, имеющая непрерывную производную. Тогда формула замены переменной .
. , t – новая переменная. Формула замены переменной при такой подстановке:
, t – новая переменная. Формула замены переменной при такой подстановке:
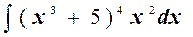 .
. .
. .
. .
.
 , (6.4.1)
, (6.4.1) сводится к нахождению другого интеграла
сводится к нахождению другого интеграла  . Применение этой формулы целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Применение этой формулы целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.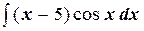 , полагая u = x –5, dv = cos xdx, найдем du = dx,
, полагая u = x –5, dv = cos xdx, найдем du = dx, 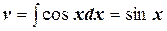 . Следовательно, применяя формулу (6.4.1), получим
. Следовательно, применяя формулу (6.4.1), получим
 ;
; ;
;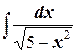 ;
; .
. .
.
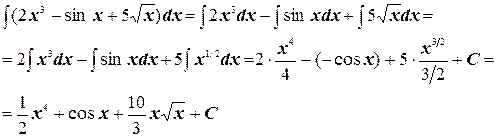

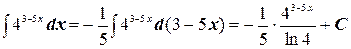 .
. ;
; ;
; ;
; .
.




 ;
; .
.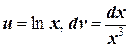 , откуда
, откуда  . Тогда по формуле (6.4.1) находим
. Тогда по формуле (6.4.1) находим
 (*)
(*) , тогда
, тогда  , следовательно,
, следовательно,

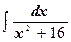 ;
; ;
; ;
; ;
; ;
; ;
; ;
;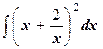 ;
; ;
; ;
; .
.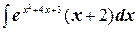 ;
; ;
;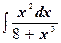 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. длину каждого такого отрезка. Вычислим значения функции f (x) в точках ck, где k= { 1, 2, …, n }.
длину каждого такого отрезка. Вычислим значения функции f (x) в точках ck, где k= { 1, 2, …, n }. (7.1.1)
(7.1.1) (7.1.2)
(7.1.2)


