
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы численного интегрирования на основе методов Эйлера и Рунге-Кутта.Содержание книги
Поиск на нашем сайте
Рассмотрим метод Эйлера - линейное приближение, использующее первые два члена ряда В методе Эйлера подынтегральная функция выносится при нижнем пределе интегрирования: yk+1=yk+f(xk,yk)h, xk=xk-1+h y(x0)=y0, yk=y(xk) В усовершенствованном методе Эйлера- Коши в первом приближении полагается:
а во втором Погрешность метода Эйлера определяется остаточным членом ряда Тейлора
т.е. R~h2 на каждом шаге вычислений. Для обеспечения сходимости шаг h следует выбирать достаточно малым. Для метода Эйлера- Коши погрешность имеет порядок h2.
Рассмотрим метод Рунге и Кутта. В основе получения вычислительных схем этого метода лежит разложение функции y(x) в ряд Тейлора с последующим преобразованием отрезка ряда к виду, не содержащему производных. На шаге h производная dy/dx=f(x,y) аппроксимируется параболой второго порядка. Здесь функция D(x,h) определяется формулой парабол Симпсона (формула Ньютона - Котеса для трех узлов):
Рассмотрим дифференциальное уравнение 1) По известным начальным условиям (хА,уА) определим значение производной в начальной точке А: Из начальной точки А проведем прямую и отметим значение ее ординаты в середине шага интегрирования h (точка В с координатами
Рис 1.2. 2) Найдем значение производной по формуле 3) По уравнению 4) По уравнению В результате построений найдем значение производных
Рис 1.3.
Будем считать, что кривая, изображающая зависимость
Значения коэффициентов a,b и с выбираются из условия прохождения параболы через точки А, М, и D. Коэффициент
Решив эти уравнения, найдем:
Проинтегрируем теперь уравнение параболы
Как видно, приращение искомой функции на шаге h при помощи описанных построений удалось представить через значения первых производных функции в четырех точках, лежащих в пределах шага интегрирования h. Запишем расчетные формулы метода Рунге- Кутта:
При условии существования у функции Для системы дифференциальных уравнений первого порядка данный алгоритм выполняется для каждого уравнения системы параллельно.
Решение контрольной задачи для одного шага интегрирования методами Эйлера и Рунге-Кутта (Проведение расчетов без ПК). Начальные условия. Для решения тестового примера на 1 шаг интегрирования системы (1.1) методами Эйлера и Рунге- Кутта задаем следующие начальные условия:
1.Шаг интегрирования h принимаем равным 0.05 секунды (h=0.05 сек.);
2. V=Vg, где Vg- скорость ЛА в момент схода с направляющих, рассчитываемая по формуле:
qg- угол наклона направляющих; qg=450=0,785 рад; tg- дульное время, рассчитываемые по формуле: Vg =
Vg =
3. q=qg- угол наклона направляющих; qg=450=0,785 рад. 4. х- начальная абсцисса, рассчитываемая по формуле: х=Sn*cosqg=4*0.785=3.96 м 5. у- начальная ордината, рассчитываемая по формуле: у= Sn*sinqg=4*0.785=3.96 м
1.4.2. Расчет системы уравнений методом Эйлера (1 шаг).
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.151.198 (0.01 с.) |

 Тейлора. Здесь искомая интегральная кривая аппроксимируется ломаной линией. Если шаг h достаточно мал, то интеграл в формуле
Тейлора. Здесь искомая интегральная кривая аппроксимируется ломаной линией. Если шаг h достаточно мал, то интеграл в формуле  можно вычислить используя теорему о среднем, т.е. вынося подынтегральную функцию из- под знака интеграла средним значением.
можно вычислить используя теорему о среднем, т.е. вынося подынтегральную функцию из- под знака интеграла средним значением.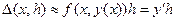 . Это приближение геометрически соответствует движению от точки x к точке х+h по касательной к кривой y(x) в точке х. Запишем расчетные формулы метода Эйлера:
. Это приближение геометрически соответствует движению от точки x к точке х+h по касательной к кривой y(x) в точке х. Запишем расчетные формулы метода Эйлера: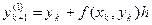

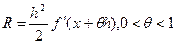

 при начальном условии (хА,уА). Выполним следующие операции:
при начальном условии (хА,уА). Выполним следующие операции: .
. (рис 1.2.)
(рис 1.2.) ).
).
 и проведем из точки А прямую
и проведем из точки А прямую 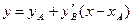 . Отметим значение ординаты этой прямой в середине шага интегрирования h (точка С с координатами
. Отметим значение ординаты этой прямой в середине шага интегрирования h (точка С с координатами  ).
). и проведем из точки А прямую
и проведем из точки А прямую  . Отметим значение ординаты этой прямой в конце шага интегрирования h (точка D с координатами
. Отметим значение ординаты этой прямой в конце шага интегрирования h (точка D с координатами  ).
). .
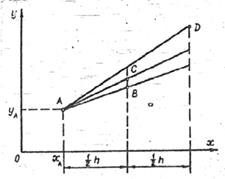
. в точках А, В,С и D. Отложим эти значения на графике рис 1.3. Как видно из графика, в точке с абсциссой
в точках А, В,С и D. Отложим эти значения на графике рис 1.3. Как видно из графика, в точке с абсциссой  получены два значения производной вместо одного. Это следствие приближенности метода. Примем в этой точке среднее значение производной:
получены два значения производной вместо одного. Это следствие приближенности метода. Примем в этой точке среднее значение производной:  . Отложив на графике (рис 1.3.) ординату
. Отложив на графике (рис 1.3.) ординату  , получим точку М.
, получим точку М.
 должна проходить через точки A,M и D. Проведем через эти три точки параболу, уравнение которой:
должна проходить через точки A,M и D. Проведем через эти три точки параболу, уравнение которой: .
.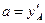 . Из уравнения параболы
. Из уравнения параболы 

 Подставив сюда полученные выше выражения для a,b,c, после приведения подобных членов для общего случая (
Подставив сюда полученные выше выражения для a,b,c, после приведения подобных членов для общего случая ( ) получим:
) получим:

 производных четвертого порядка погрешность метода является величиной порядка h5.
производных четвертого порядка погрешность метода является величиной порядка h5. , где
, где и tg =
и tg =  , где
, где =
= 





