Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Активный участок траектории ЛАСодержание книги Поиск на нашем сайте
Дополнительные параметры
Движение по направляющим
Активный участок траектории ЛА
Пассивный участок траектории ЛА.
Глава 1
1.Разработка Компьютерной модели расчета траектории неуправляемого летательного аппарата. Постановка задач. Анализ и представление исходных данных.
В этой главе рассмотрены следующие задачи: 1. Разработка компьютерной модели расчета траектории неуправляемого ЛА, используя методы численного интегрирования Эйлера и Рунге-Кутта. 2. Расчет траектории пассивного участка полета неуправляемого ЛА с использованием параболической теории. Траектория полета неуправляемого ЛА (снаряда РСЗО) состоит из трех характерных участков: 1. движение по направляющим; 2. активный участок; 3. пассивный участок.
Расчет дополнительных параметров: 1. Секундный массовый расход (q) рассчитан по формуле:
2. Тяга двигателя (R) рассчитана по формуле: R=Ue*q 3. Коэффициент лобового сопротивления рассчитан по формуле: Cx=Cx(M)*i, где Cx=Cx(M)-коэффициент лобового сопротивления эталонного ЛА. Принимаем Cx =0.3. 4. Площадь миделя ЛА рассчитана по формуле:
5. Закон изменения массовой плотности воздуха от высоты полета принимаем в виде 6. Закон изменения массы принимаем в виде m= m0-q*t.
Модель динамики неуправляемого ЛА. Движение ЛА по направляющим. При расчете движения по направляющем принимается во внимание действие на ЛА следующих сил: R- тяга, G- вес ЛА, F- реакция направляющих, которая состоит из силы трения Fтр и нормальной составляющей N. Аэродинамическими силами при расчете движения по направляющим обычно пренебрегают.
Кроме того, в идеальном случае направляющие принимаются жесткими и недеформированными. Расчетная схема движения представлена на рисунке 1.1.
Рис 1.1.
Уравнение движения ЛА на направляющих в проекции на направление скорости запишется в виде
где f- коэффициент трения скольжения, m=m0-Q*t – принимаемый в работе закон изменения массы ЛА, G=m*g. Записывая уравнение движения в нормальной форме Коши, получаем
Последовательно интегрируя уравнение с учетом соотношения ds/dt=v, находим
Полагая в формулах t=td, получаем выражение для дульной скорости Vd и длины направляющих:
Если задана длина направляющих Sh, то, решая численно уравнение, определим td. Для этого уравнение запишем в виде
Если пренебречь изменением массы при движении ЛА по направляющим, то, заменяя массу ЛА средним значением m= mср, получаем По этим формулам можно приближенно найти vd и td.
Примечание: 1. Коэффициент трения скольжения ЛА об направляющие f равен 0.15 (f=0.15). 2. Изменением массы при движении ЛА по направляющим пренебрегаем. Активный участок полета ЛА. При расчете активного участка полета ЛА принимают следующие допущения: 1. угол атаки равен нулю. 2. тяга R постоянна. При сделанных допущениях уравнения для расчета траектории ЛА на активном участке полета запишутся в виде следующей системы дифференциальных уравнений первого порядка:
Здесь X=0.5*Cx*Ro*S*V – сила лобового сопротивления. Остальные элементы системы были указаны выше. Пассивный участок полета ЛА. При расчете пассивного участка полета ЛА также используется система (1.1). При этом: 1. тяга R равна нулю (R=0). 2. поверхность Земли представляется в виде бесконечной плоскости. 3. масса ЛА постоянна (m= m-mt=const).
Решение контрольной задачи для одного шага интегрирования методами Эйлера и Рунге-Кутта (Проведение расчетов без ПК). Начальные условия. Для решения тестового примера на 1 шаг интегрирования системы (1.1) методами Эйлера и Рунге- Кутта задаем следующие начальные условия:
1.Шаг интегрирования h принимаем равным 0.05 секунды (h=0.05 сек.);
2. V=Vg, где Vg- скорость ЛА в момент схода с направляющих, рассчитываемая по формуле:
qg- угол наклона направляющих; qg=450=0,785 рад;
tg- дульное время, рассчитываемые по формуле: Vg =
Vg =
3. q=qg- угол наклона направляющих; qg=450=0,785 рад. 4. х- начальная абсцисса, рассчитываемая по формуле: х=Sn*cosqg=4*0.785=3.96 м 5. у- начальная ордината, рассчитываемая по формуле: у= Sn*sinqg=4*0.785=3.96 м
1.4.2. Расчет системы уравнений методом Эйлера (1 шаг). Движение по направляющим. Результатами расчета траекторных параметров данного участка траектории являются значения дульной скорости (vd) и дульного времени (td). Результаты расчета приведены в таблице 1.4.: Таблица 1.4
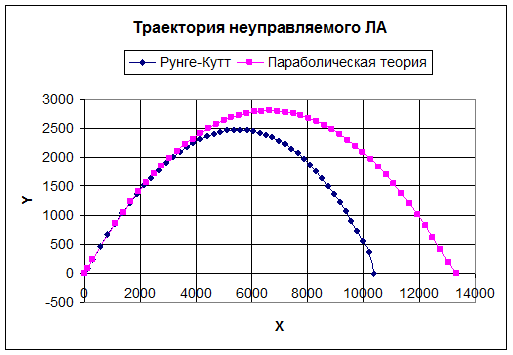
Приложение 1. Графики 1. V(t) методами численного интегрирования и по параболической теории. 2. θ(t) методами численного интегрирования и по параболической теории. 3. y(x) (Метод Эйлера и параболическая теория). 4. y(x) (Метод Рунге-Кутта и параболическая теория).
Приложение 2. Текст программы, разработанной для интегрирования методами Эйлера и Рунге-Кутта. (Программа выполнена на Visual Basic 6.0 Professional Edition)
Option Base 1 Const r0 = 1.23 Dim r As Double Dim y As Double Dim x As Double Dim V As Double Dim Q As Double Dim Xx As Double Dim m As Double Dim Yg As Double Dim Xg As Double Dim Cx As Double Dim Vg As Double Dim S As Double Dim Mn As Double Dim Rashod As Double Dim Tg As Double Dim Rs As Double Dim T As Double Dim h As Double Dim Qg As Double Dim i As Double Dim K(4, 4) As Double Dim str As String Dim j As Double
Private Sub Command1_Click() lbl.ForeColor = &HFF& lbl.Caption = "идет расчет" DoEvents Yg = CDbl(Text4.Text) * Sin(CDbl(Text3.Text)) Xg = CDbl(Text4.Text) * Cos(CDbl(Text3.Text)) Cx = CDbl(Text5.Text) Vg = CDbl(Text1.Text) S = CDbl(Text6.Text) Mn = CDbl(Text17.Text) Rashod = CDbl(Text18.Text) Tg = CDbl(Text2.Text) Rs = CDbl(Text19.Text) T = CDbl(Text16.Text) h = CDbl(Text7.Text) Qg = CDbl(Text3.Text) Text33.Text = "" Text34.Text = "" Text36.Text = "" Text40.Text = "" Text38.Text = ""
'---------------------------------- 'Активный участок траектории полета 'Эйлер x = Xg y = Yg V = Vg Q = Qg j = Tg For i = Tg To T Step h r = r0 * Exp(-y / 7800) Xx = 0.5 * Cx * r * S * V ^ 2 m = Mn - Rashod * i V = V + h * (Rs - 9.81 * m * Sin(Q) - Xx) / m Q = Q - h * 9.81 * Cos(Q) / V x = x + h * V * Cos(Q) y = y + h * V * Sin(Q) If Option1.Value = True And Round(i, 2) = Round(j, 2) Then j = j + 1 Text33.Text = Text33.Text & Round(i, 2) & vbCrLf Text34.Text = Text34.Text & Round(V, 1) & vbCrLf Text36.Text = Text36.Text & Round(Q, 3) & vbCrLf Text40.Text = Text40.Text & Round(x, 0) & vbCrLf Text38.Text = Text38.Text & Round(y, 0) & vbCrLf End If If i = Tg Then str = "Значения коэфициентов" & vbCrLf & "на первом шаге Э" & vbCrLf str = str & "V = " & Round(V, CLng(Text21.Text)) & vbCrLf str = str & "Q = " & Round(Q, CLng(Text21.Text)) & vbCrLf str = str & "X = " & Round(x, CLng(Text21.Text)) & vbCrLf str = str & "Y = " & Round(y, CLng(Text21.Text)) & vbCrLf & vbCrLf End If Next i Text8.Text = Round(V, CLng(Text21.Text)) Text9.Text = Round(Q, CLng(Text21.Text)) Text10.Text = Round(x, CLng(Text21.Text)) Text11.Text = Round(y, CLng(Text21.Text)) '----------------------------- 'Рунге-Кутт x = Xg y = Yg V = Vg Q = Qg j = Tg For i = Tg To T Step h r = r0 * Exp(-y / 7800) Xx = 0.5 * Cx * r * S * V ^ 2 m = Mn - Rashod * i K(1, 1) = h * (Rs - 9.81 * m * Sin(Q) - Xx) / m K(1, 2) = -9.81 * h * Cos(Q) / V K(1, 3) = h * V * Cos(Q) K(1, 4) = h * V * Sin(Q)
r = r0 * Exp(-(y + 0.5 * K(1, 4)) / 7800) Xx = 0.5 * Cx * r * S * (V + 0.5 * K(1, 1)) ^ 2 m = Mn - Rashod * (i + h / 2) K(2, 1) = h * (Rs - 9.81 * m * Sin(Q + K(1, 2) / 2) - Xx) / m K(2, 2) = -9.81 * h * Cos(Q + K(1, 2) / 2) / (V + K(1, 1) / 2) K(2, 3) = h * (V + K(1, 1) / 2) * Cos(Q + K(1, 2) / 2) K(2, 4) = h * (V + K(1, 1) / 2) * Sin(Q + K(1, 2) / 2)
r = r0 * Exp(-(y + 0.5 * K(2, 4)) / 7800) Xx = 0.5 * Cx * r * S * (V + 0.5 * K(2, 1)) ^ 2 m = Mn - Rashod * (i + h / 2) K(3, 1) = h * (Rs - 9.81 * m * Sin(Q + K(2, 2) / 2) - Xx) / m K(3, 2) = -9.81 * h * Cos(Q + K(2, 2) / 2) / (V + K(2, 1) / 2) K(3, 3) = h * (V + K(2, 1) / 2) * Cos(Q + K(2, 2) / 2) K(3, 4) = h * (V + K(2, 1) / 2) * Sin(Q + K(2, 2) / 2)
r = r0 * Exp(-(y + K(3, 4)) / 7800) Xx = 0.5 * Cx * r * S * (V + K(3, 1)) ^ 2 m = Mn - Rashod * (i + h) K(4, 1) = h * (Rs - 9.81 * m * Sin(Q + K(3, 2)) - Xx) / m K(4, 2) = -9.81 * h * Cos(Q + K(3, 2)) / (V + K(3, 1)) K(4, 3) = h * (V + K(3, 1)) * Cos(Q + K(3, 2))
K(4, 4) = h * (V + K(3, 1)) * Sin(Q + K(3, 2))
V = V + (K(1, 1) + K(4, 1) + 2 * (K(2, 1) + K(3, 1))) / 6 Q = Q + (K(1, 2) + K(4, 2) + 2 * (K(2, 2) + K(3, 2))) / 6 x = x + (K(1, 3) + K(4, 3) + 2 * (K(2, 3) + K(3, 3))) / 6 y = y + (K(1, 4) + K(4, 4) + 2 * (K(2, 4) + K(3, 4))) / 6
If Option2.Value = True And Round(i, 2) = Round(j, 2) Then j = j + 1 Text33.Text = Text33.Text & Round(i, 2) & vbCrLf Text34.Text = Text34.Text & Round(V, 1) & vbCrLf Text36.Text = Text36.Text & Round(Q, 3) & vbCrLf Text40.Text = Text40.Text & Round(x, 0) & vbCrLf Text38.Text = Text38.Text & Round(y, 0) & vbCrLf End If
If i = Tg Then str = str & "Значения коэффициентов" & vbCrLf & "на первом шаге Р-К" & vbCrLf str = str & "K(1,1) = " & Round(K(1, 1), CLng(Text21.Text)) & vbCrLf str = str & "K(1,2) = " & Round(K(1, 2), CLng(Text21.Text)) & vbCrLf str = str & "K(1,3) = " & Round(K(1, 3), CLng(Text21.Text)) & vbCrLf str = str & "K(1,4) = " & Round(K(1, 4), CLng(Text21.Text)) & vbCrLf str = str & "K(2,1) = " & Round(K(2, 1), CLng(Text21.Text)) & vbCrLf str = str & "K(2,2) = " & Round(K(2, 2), CLng(Text21.Text)) & vbCrLf str = str & "K(2,3) = " & Round(K(2, 3), CLng(Text21.Text)) & vbCrLf str = str & "K(2,4) = " & Round(K(2, 4), CLng(Text21.Text)) & vbCrLf str = str & "K(3,1) = " & Round(K(3, 1), CLng(Text21.Text)) & vbCrLf str = str & "K(3,2) = " & Round(K(3, 2), CLng(Text21.Text)) & vbCrLf str = str & "K(3,3) = " & Round(K(3, 3), CLng(Text21.Text)) & vbCrLf str = str & "K(3,4) = " & Round(K(3, 4), CLng(Text21.Text)) & vbCrLf str = str & "K(4,1) = " & Round(K(4, 1), CLng(Text21.Text)) & vbCrLf str = str & "K(4,2) = " & Round(K(4, 2), CLng(Text21.Text)) & vbCrLf str = str & "K(4,3) = " & Round(K(4, 3), CLng(Text21.Text)) & vbCrLf str = str & "K(4,4) = " & Round(K(4, 4), CLng(Text21.Text)) & vbCrLf str = str & "V = " & Round(V, CLng(Text21.Text)) & vbCrLf str = str & "Q = " & Round(Q, CLng(Text21.Text)) & vbCrLf str = str & "X = " & Round(x, CLng(Text21.Text)) & vbCrLf str = str & "Y = " & Round(y, CLng(Text21.Text)) Text20.Text = str End If
Next i Text12.Text = Round(V, CLng(Text21.Text)) Text13.Text = Round(Q, CLng(Text21.Text)) Text14.Text = Round(x, CLng(Text21.Text)) Text15.Text = Round(y, CLng(Text21.Text)) '---------------------------------- 'Пассивный участок траектории полета 'Эйлер V = CDbl(Text8.Text) Q = CDbl(Text9.Text) x = CDbl(Text10.Text) y = CDbl(Text11.Text) i = T m = Mn - Rashod * T j = T Do While y > 0 r = r0 * Exp(-y / 7800) Xx = 0.5 * Cx * r * S * V ^ 2 V = V - h * (9.81 * m * Sin(Q) + Xx) / m Q = Q - h * 9.81 * Cos(Q) / V x = x + h * V * Cos(Q) y = y + h * V * Sin(Q)
If Option1.Value = True And Round(i, 2) = Round(j, 2) Then j = j + 1 Text33.Text = Text33.Text & Round(i, 2) & vbCrLf Text34.Text = Text34.Text & Round(V, 1) & vbCrLf Text36.Text = Text36.Text & Round(Q, 3) & vbCrLf Text40.Text = Text40.Text & Round(x, 0) & vbCrLf Text38.Text = Text38.Text & Round(y, 0) & vbCrLf End If
If Abs(Q) < 0.001 Then str = "Значения параметров" & vbCrLf & "в наивысшей точке траектории" & vbCrLf & "методом Эйлера" & vbCrLf str = str & "t = " & Round(i, 2) & vbCrLf str = str & "V = " & Round(V, CLng(Text21.Text)) & vbCrLf str = str & "Q = 0" & vbCrLf str = str & "X = " & Round(x, CLng(Text21.Text)) & vbCrLf str = str & "Y = " & Round(y, CLng(Text21.Text)) & vbCrLf & vbCrLf End If i = i + h Loop Text25.Text = Round(V, CLng(Text21.Text)) Text24.Text = Round(Q, CLng(Text21.Text))
Text23.Text = Round(x, CLng(Text21.Text)) Text22.Text = Round(y, CLng(Text21.Text)) Text31.Text = Round(i, 2) '----------------------------- 'Рунге-Кутт V = CDbl(Text12.Text) Q = CDbl(Text13.Text) x = CDbl(Text14.Text) y = CDbl(Text15.Text) i = T j = T m = Mn - Rashod * T Do While y > 0 r = r0 * Exp(-y / 7800) Xx = 0.5 * Cx * r * S * V ^ 2 K(1, 1) = h * (-9.81 * m * Sin(Q) - Xx) / m K(1, 2) = -9.81 * h * Cos(Q) / V K(1, 3) = h * V * Cos(Q) K(1, 4) = h * V * Sin(Q)
r = r0 * Exp(-(y + 0.5 * K(1, 4)) / 7800) Xx = 0.5 * Cx * r * S * (V + 0.5 * K(1, 1)) ^ 2 K(2, 1) = h * (-9.81 * m * Sin(Q + K(1, 2) / 2) - Xx) / m K(2, 2) = -9.81 * h * Cos(Q + K(1, 2) / 2) / (V + K(1, 1) / 2) K(2, 3) = h * (V + K(1, 1) / 2) * Cos(Q + K(1, 2) / 2) K(2, 4) = h * (V + K(1, 1) / 2) * Sin(Q + K(1, 2) / 2)
r = r0 * Exp(-(y + 0.5 * K(2, 4)) / 7800) Xx = 0.5 * Cx * r * S * (V + 0.5 * K(2, 1)) ^ 2 K(3, 1) = h * (-9.81 * m * Sin(Q + K(2, 2) / 2) - Xx) / m K(3, 2) = -9.81 * h * Cos(Q + K(2, 2) / 2) / (V + K(2, 1) / 2) K(3, 3) = h * (V + K(2, 1) / 2) * Cos(Q + K(2, 2) / 2) K(3, 4) = h * (V + K(2, 1) / 2) * Sin(Q + K(2, 2) / 2)
r = r0 * Exp(-(y + K(3, 4)) / 7800) Xx = 0.5 * Cx * r * S * (V + K(3, 1)) ^ 2 K(4, 1) = h * (-9.81 * m * Sin(Q + K(3, 2)) - Xx) / m K(4, 2) = -9.81 * h * Cos(Q + K(3, 2)) / (V + K(3, 1)) K(4, 3) = h * (V + K(3, 1)) * Cos(Q + K(3, 2)) K(4, 4) = h * (V + K(3, 1)) * Sin(Q + K(3, 2))
V = V + (K(1, 1) + K(4, 1) + 2 * (K(2, 1) + K(3, 1))) / 6 Q = Q + (K(1, 2) + K(4, 2) + 2 * (K(2, 2) + K(3, 2))) / 6 x = x + (K(1, 3) + K(4, 3) + 2 * (K(2, 3) + K(3, 3))) / 6 y = y + (K(1, 4) + K(4, 4) + 2 * (K(2, 4) + K(3, 4))) / 6
If Option2.Value = True And Round(i, 2) = Round(j, 2) Then j = j + 1 Text33.Text = Text33.Text & Round(i, 2) & vbCrLf Text34.Text = Text34.Text & Round(V, 1) & vbCrLf Text36.Text = Text36.Text & Round(Q, 3) & vbCrLf Text40.Text = Text40.Text & Round(x, 0) & vbCrLf Text38.Text = Text38.Text & Round(y, 0) & vbCrLf End If
If Abs(Q) < 0.001 Then str = str & "Значения параметров" & vbCrLf & "в наивысшей точке траектории" & vbCrLf & "методом Рунге-Кутта" & vbCrLf str = str & "t = " & Round(i, 2) & vbCrLf str = str & "V = " & Round(V, CLng(Text21.Text)) & vbCrLf str = str & "Q = 0" & vbCrLf str = str & "X = " & Round(x, CLng(Text21.Text)) & vbCrLf str = str & "Y = " & Round(y, CLng(Text21.Text)) Text30.Text = str End If i = i + h Loop Text29.Text = Round(V, CLng(Text21.Text)) Text28.Text = Round(Q, CLng(Text21.Text)) Text27.Text = Round(x, CLng(Text21.Text)) Text26.Text = Round(y, CLng(Text21.Text)) Text32.Text = Round(i, 2)
lbl.ForeColor = &HC000& lbl.Caption = "Расчет выполнен" End Sub
Private Sub Command2_Click() End End Sub
1. Бахвалов Н.С. Численные методы. т.1., М.: Наука, 1975. 2. Волков Е.А. Численные методы. М.: Наука, 1982 3. Шалыгин А.С. и др. Автоматизация расчета траекторий ЛА: Учебн. пособие. – Л., 1990. 4. http://a5.bstu.spb.su
Дополнительные параметры
Движение по направляющим
Активный участок траектории ЛА
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 949; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.40.40 (0.008 с.) |


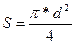
 , где ro= 1.23- плотность воздуха на уровне моря; высота y в формуле берется в метрах.
, где ro= 1.23- плотность воздуха на уровне моря; высота y в формуле берется в метрах.






 (1.1)
(1.1) , где
, где и tg =
и tg =  , где
, где =
= 


 , град
, град