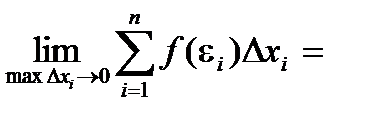Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод интегрирования подстановкой (заменой переменной)Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Пусть требуется вычислить интеграл Тогда dx = j'(t)dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой
Эта формула также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х. Иногда целесообразно подбирать подстановку в виде t = j(х), тогда Пример. Найти Замена
Метод интегрирования по частям
Пусть u = u(x), v = v(x) – функции, имеющие непрерывные производные. Тогда d(uv) = udv + vdu. Интегрируя это равенство, получим
Порученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Определенный интеграл Определение. Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма Обозначение: Определение. Если для функции f(x) существует предел
то функция называется интегрируемой на отрезке [a, b].
Также верны утверждения:
Теорема. Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла. 1) 2) 3) 4) Если f(x) £ j(x) на отрезке [a, b] a < b, то 5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:
6) Для произвольных чисел a, b, c справедливо равенство:
7)
|
|||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |
 f(x) dx. Сделаем подстановку x = j(t), где j(t) – функция, имеющая непрерывную производную.
f(x) dx. Сделаем подстановку x = j(t), где j(t) – функция, имеющая непрерывную производную.
 =
=  f(t)dt, где t =j(х). Другими словами, формулу можно применять справа налево.
f(t)dt, где t =j(х). Другими словами, формулу можно применять справа налево.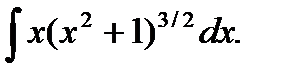
 Получаем:
Получаем: .
.
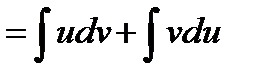 или
или  .
.
 udv к вычислению интеграла
udv к вычислению интеграла  стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b]. , а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
, а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.